<?xml version="1.0" encoding="utf-8"?>
<rss xmlns:atom="http://www.w3.org/2005/Atom" version="2.0"><channel><title>ASKSAGE: Sage Q&A Forum - RSS feed</title><link>https://ask.sagemath.org/questions/</link><description>Q&A Forum for Sage</description><atom:link href="https://ask.sagemath.org/feeds/rss/" rel="self"></atom:link><language>en</language><copyright>Copyright Sage, 2010. Some rights reserved under creative commons license.</copyright><lastBuildDate>Tue, 19 Nov 2024 16:44:05 +0100</lastBuildDate><item><title>apply Permutation cycles to a letters list</title><link>https://ask.sagemath.org/question/80292/apply-permutation-cycles-to-a-letters-list/</link><description> Hi
Sorry for this very basic question, but how to apply the Permutation function to a list of letters ?
I think it should exist a simplest way than the the cooking below.
I searched the web, without success !
def applyGen(ge,dic) :
return [ge[dic.get(e)] for e in dic.keys() ]
def decrement_dic(dic):
return {k - 1: v - 1 for k, v in dic.items()}
lettersL=['a','b','c','d','e','f','g','h']
test=Permutation((1,5,8,4),(2,6,7,3))
dicD=decrement_dic(test.dict())
applyGen(lettersL,dicD)</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">ortollj</dc:creator><pubDate>Tue, 19 Nov 2024 16:44:05 +0100</pubDate><guid>https://ask.sagemath.org/question/80292/</guid></item><item><title>Converting between sized and unsized Permutations</title><link>https://ask.sagemath.org/question/75905/converting-between-sized-and-unsized-permutations/</link><description>Sage has two similar classes of permutations with the names **Standard permutations** and **Standard permutations of n**. I wonder how to convert elements (of appropriate size) from one class to the other, and back.
Here an example of permutations from the two classes:
p = next(iter(Permutations(5)))
print('p =', p)
print(p.parent())
q = Permutation([1,2,3,4,5])
print('q =', q)
print(q.parent())
which prints
p = [1, 2, 3, 4, 5]
Standard permutations of 5
q = [1, 2, 3, 4, 5]
Standard permutations
How to add size to `q` and how to remove one from `p` most naturally? My solutions look ugly:
q_ = Permutations(len(q))(q)
p_ = Permutation(list(p))
</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Max Alekseyev</dc:creator><pubDate>Sat, 10 Feb 2024 14:53:33 +0100</pubDate><guid>https://ask.sagemath.org/question/75905/</guid></item><item><title>Efficient way to compute all possible permutations that sort a list</title><link>https://ask.sagemath.org/question/74271/efficient-way-to-compute-all-possible-permutations-that-sort-a-list/</link><description>I'm looking for a good way to compute all the possible permutations that sort a list. For example, if the list is [3,4,3,2,4] I would want the permutations to be: [4,1,3,2,5], [4,1,3,5,2], [4,3,1,2,5], [4,3,1,5,2]. I'm well aware of how to get a permutation that sorts the list, one can use argsort or standard_permutation(), but neither of these will return all such permutations.
I can also, of course, come up with something stupid myself, but I worry it won't be efficient and I wish to do this for a largeish number of arrays.
Edit: Here is my best attempt to code this. Essentially, I find one permutation using the standard 'sorted' python function, and then find all permutations that preserve the sorted list, and then multiply the two permutations. I just feel like this is a really stupid way to do this that will slow my program down. Especially if the list is long, this is going to involve checking a bunch of unnecessary permutations.
dP = [3,4,3,2,4]
sorted_enumerate_dP = sorted(enumerate(dP,1), key=lambda x: x[1])
sorted_dP = [pair[1] for pair in sorted_enumerate_dP]
initial_perm = Permutation([pair[0] for pair in sorted_enumerate_dP])
further_perms = []
for p in Permutations(len(sorted_dP)):
new_dP=[sorted_dP[i-1] for i in p]
if new_dP == sorted_dP:
further_perms+=[p]
perms = []
for p in further_perms:
perms += [Permutation([initial_perm[i-1] for i in p])]
print(perms)
The output is indeed [[4, 1, 3, 2, 5], [4, 1, 3, 5, 2], [4, 3, 1, 2, 5], [4, 3, 1, 5, 2]], as I want.</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Quinten87</dc:creator><pubDate>Fri, 10 Nov 2023 21:08:20 +0100</pubDate><guid>https://ask.sagemath.org/question/74271/</guid></item><item><title>Unexpected error with sign() function in SageMath</title><link>https://ask.sagemath.org/question/73186/unexpected-error-with-sign-function-in-sagemath/</link><description>I have the following rather strange issue with SageMath. More specifically the problem seem to be related with SageMath libraries dealing with permutations and Lie algebras. Here is the part of the code which does not compile properly for some reason:
gl = lie_algebras.gl(QQ, 4)
Ugl = gl.pbw_basis()
E = matrix(Ugl, 4, 4, Ugl.gens())
for sigma in Permutations(4):
for tau in Permutations(4):
pr = sigma.signature() * tau.signature()
for i in range(4):
pr = pr * E[sigma[i] - 1, tau[i] - 1]
The interesting thing is that while the code above does not work well, the issue could be resolved just by adding `1 * `, see below:
gl = lie_algebras.gl(QQ, 4)
Ugl = gl.pbw_basis()
E = matrix(Ugl, 4, 4, Ugl.gens())
for sigma in Permutations(4):
for tau in Permutations(4):
pr = sigma.signature() * tau.signature()
for i in range(4):
pr = 1 * pr * E[sigma[i] - 1, tau[i] - 1]
My experiments show that there is some issue with SageMath function `signature()` since if I replace the line `pr = sigma.signature() * tau.signature()` with `pr = 1`, then both versions compile successfully. The final block of the error message for the first excerpt is as follows:
/usr/lib/python3/dist-packages/sage/algebras/lie_algebras/poincare_birkhoff_witt.py in _act_on_(self, x, self_on_left)
513 # Try the _acted_upon_ first as it might have a direct PBW action
514 # implemented that is faster
--> 515 ret = x._acted_upon_(self, not self_on_left)
516 if ret is not None:
517 return ret
AttributeError: 'int' object has no attribute '_acted_upon_'
Therefore, it might be the case that there is something strange happening with the action of integers on element of Lie algebras (some type-related issue?).
Of course, since the second version works I can proceed, but it looks weird and I would be really interested in understanding the source of this error (to avoid similar ones in the future).
**Comment.** I did no realize at first that for SageMath there is a special Q&A forum, so initially I posted it on SE.
</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">richrow23</dc:creator><pubDate>Wed, 06 Sep 2023 19:04:54 +0200</pubDate><guid>https://ask.sagemath.org/question/73186/</guid></item><item><title>simultaneous conjugacy in Sn</title><link>https://ask.sagemath.org/question/66368/simultaneous-conjugacy-in-sn/</link><description> Is there a built-in function in sage to determine whether two pairs (a,b) and (c,d) of elements of S_n (symmetric group of n letters) are simultaneously conjugate, i.e. checking whether there exists x such that
xa=cx and xb=dx ?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">matrixman</dc:creator><pubDate>Mon, 13 Feb 2023 16:20:54 +0100</pubDate><guid>https://ask.sagemath.org/question/66368/</guid></item><item><title>Multiply Arbitrary Permutations</title><link>https://ask.sagemath.org/question/61930/multiply-arbitrary-permutations/</link><description>Is there a way to multiply arbitrary permutations?
sage: P=Permutations(var('x y z'));P
Permutations of the set [x, y, z]
sage: P[1];P[2]
[x, z, y]
[y, x, z]
But now
sage: P[1]*P[2]
gives an error:
TypeError: unsupported operand parent(s) for *: 'Permutations of the set [x, y, z]' and 'Permutations of the set [x, y, z]'
I can't even evaluate such a permutation at an element.
sage: P[1](x)
results in
TypeError: 'Permutations_set_with_category.element_class' object is not callable</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Thrash</dc:creator><pubDate>Tue, 12 Apr 2022 15:04:36 +0200</pubDate><guid>https://ask.sagemath.org/question/61930/</guid></item><item><title>Action of Permutations on Points, maybe with GAP?</title><link>https://ask.sagemath.org/question/61794/action-of-permutations-on-points-maybe-with-gap/</link><description>I cannot seem to figure out how to make Sage act on a point with a permutation. For example, if I act on the integer 17 with the permutation (5,17), the result is 17. This works fine in vanilla GAP:
gap> 17^(17,5);
5
gap> OnPoints(17,(17,5));
5
But I can't seem to determine the Sage command - does Sage only have the ability to multiply permutations with p1.action(p2), or can it do what I'm getting at here?
I tried accessing the GAP interface directly with gap.console(), but the resulted in the kernel hanging. Actually, even SageMathCell can't seem to figure out what gap.console() is supposed to do.
Anyone have any thoughts?
EDIT: Learning more about how Sage calls GAP is not helping....
sage: libgap.eval(G:=FreeGroup(3))
<free group on the generators [ x0, x1, x2 ]>
sage: libgap.eval(OnPoints(3,(1,2,3)))
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
<ipython-input-3-0f49a104e96c> in <module>
----> 1 libgap.eval(OnPoints(Integer(3),(Integer(1),Integer(2),Integer(3))))
NameError: name 'OnPoints' is not defined</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">thethinker</dc:creator><pubDate>Sat, 02 Apr 2022 02:31:40 +0200</pubDate><guid>https://ask.sagemath.org/question/61794/</guid></item><item><title>Code to find separating set in SageMath of a given Graph</title><link>https://ask.sagemath.org/question/47381/code-to-find-separating-set-in-sagemath-of-a-given-graph/</link><description>Given a Graph $G$ how can I find the separating set of the Graph?
Suppose I am given this graph
G = Graph({1: [2, 3, 4, 5],
2: [1, 3, 4, 5],
3: [1, 2, 4, 5],
4: [1, 2, 3],
5: [1, 2, 3]})
I want to find the set of vertices whose removal disconnects the graph.
I found that the vertex connectivity of $G$ is 2.
Looking at the graph, the smallest set of vertices
whose removal disconnects the graph is $(1, 2, 3)$.
But how to find it using a code in SageMath?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Captcha</dc:creator><pubDate>Sun, 04 Aug 2019 14:52:38 +0200</pubDate><guid>https://ask.sagemath.org/question/47381/</guid></item><item><title>Find the longest word in a symmetric group which satisfies a certain property.</title><link>https://ask.sagemath.org/question/60799/find-the-longest-word-in-a-symmetric-group-which-satisfies-a-certain-property/</link><description>Let $A, B$ be two list of equal length $k$, where $A$ is weakly increasing. For example, $A=[1, 1, 2, 3, 3, 4]$, $B=[12, 9, 10, 15, 15, 14]$.
Define $m_{A,B}$ to be the multiset of pairs $[ A_i, B_i ]$, $i \in k$, (this is a multi-set of pairs of integers, not a list of pairs, so the order of pairs in $m_{A,B}$ does not matter).
By a result in symmetric group, there is a unique element with maximal length (length of the reduced word) in the symmetric group $S_k$ ($k$ is the length of $A$) such that $m_{A,w(sorted(B))} = m_{A,B}$, where $sorted(B)$ is to sorted B such that it is weakly increasing, and the action of $w=s_{i_1} \cdots s_{i_m}$ on a list $L$ is defined by: $s_j(L)$ means exchanging the jth and j+1th elements of $L$, and for $w,w' \in S_k$, $w w'(L) = w(w'(L))$.
There is a method to compute the longest word $w$ by checking all elements in $S_k$. But it takes a long time when $k$ is large. The following function works fine and returns correct result.
def LongestPerm(A,Bsorted,B):
k = len(A)
S = set([(A[i],B[i]) for i in range(k)])
W = WeylGroup('A'+str(k-1), prefix = 's')
winner = W.one()
for w in W:
wstr = w.inverse().to_permutation_string()
if set([(A[int(wstr[i])-1],Bsorted[i]) for i in range(k)]) == S:
if w.length()>winner.length():
winner = w
return winner
In the example that
A=[1, 1, 2, 3, 3, 4]
B=[12, 9, 10, 15, 15, 14]
we have
w=s4*s5*s4*s2*s1
Is there some method to compute $w$ faster (without checking all elements of $S_k$)? Thank you very much.</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">lijr07</dc:creator><pubDate>Mon, 24 Jan 2022 09:35:15 +0100</pubDate><guid>https://ask.sagemath.org/question/60799/</guid></item><item><title>How to find a permutation which sends a given list to another given list in SageMath?</title><link>https://ask.sagemath.org/question/60779/how-to-find-a-permutation-which-sends-a-given-list-to-another-given-list-in-sagemath/</link><description>Given two list L1, L2, say
L1=[1,2,5,6,3,4,4,8,2,1,9,3,2]
L2=[1,2,2,5,6,4,3,4,8,9,1,2,3]
How to find a permutation w in $S_{13}$ such that w(L1) = L2 in python?
Here $w=s_{i_1} \cdots s_{i_k}$ for some $k$, and each $s_{j}$ acts on L1 by exchanging the jth and j+1th element of L1.
Thank you very much.</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">lijr07</dc:creator><pubDate>Sun, 23 Jan 2022 15:17:09 +0100</pubDate><guid>https://ask.sagemath.org/question/60779/</guid></item><item><title>Change order of multiplication/composition in SymmetricGroup</title><link>https://ask.sagemath.org/question/60052/change-order-of-multiplicationcomposition-in-symmetricgroup/</link><description>How can I change the order of multiplication/composition of elements in the symmetric group?
Example:
sage: S=SymmetricGroup(4)
sage: a=S((1,2))
sage: b=S((2,3))
sage: c=S((3,4))
sage: a*b*c
(1,4,3,2)
How can I change this behavior so that I can execute `a*b*c` and the output will be `(1,2,3,4)`? I want to keep using the star `*`, not an inconvenient command like `a.__rmul__(b).__rmul__(c)`, otherwise I would have to rewrite all my code.
</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Thrash</dc:creator><pubDate>Fri, 03 Dec 2021 13:40:00 +0100</pubDate><guid>https://ask.sagemath.org/question/60052/</guid></item><item><title>entering permutation as product of not necessarily disjoint cycles</title><link>https://ask.sagemath.org/question/59114/entering-permutation-as-product-of-not-necessarily-disjoint-cycles/</link><description>I was expecting to get the identity when I did the following:
sage: G = SymmetricGroup(3)
sage: G('(1,2)(1,2)')
but I get (1,2).
How to tell Sage to compute a product of not necessarily disjoint cycles?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">ykm</dc:creator><pubDate>Tue, 21 Sep 2021 18:39:30 +0200</pubDate><guid>https://ask.sagemath.org/question/59114/</guid></item><item><title>Permutations and transpositions</title><link>https://ask.sagemath.org/question/58820/permutations-and-transpositions/</link><description> Is it possible in Sage to get the decomposition in transpositions of a permutation?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">oldani</dc:creator><pubDate>Fri, 03 Sep 2021 13:06:23 +0200</pubDate><guid>https://ask.sagemath.org/question/58820/</guid></item><item><title>Testing whether a list of permutations avoids two permutations</title><link>https://ask.sagemath.org/question/58461/testing-whether-a-list-of-permutations-avoids-two-permutations/</link><description>I have a list of $n$-permutations in Sage, for example:
U=[[2, 3, 1, 4, 5], [2, 4, 1, 3, 5], [2, 5, 1, 3, 4], [2, 1, 3, 4, 5], [1, 3, 4, 2, 5], [1, 3, 5, 2, 4], [1, 3, 2, 4, 5], [3, 1, 4, 2, 5], [3, 4, 1, 2, 5], [3, 5, 1, 2, 4], [3, 1, 2, 4, 5], [1, 2, 4, 5, 3], [1, 2, 4, 3, 5], [1, 4, 2, 5, 3], [1, 4, 5, 2, 3], [1, 4, 2, 3, 5], [4, 1, 2, 5, 3], [4, 1, 5, 2, 3], [4, 5, 1, 2, 3], [4, 1, 2, 3, 5], [1, 2, 3, 5, 4], [1, 2, 5, 3, 4], [1, 5, 2, 3, 4], [5, 1, 2, 3, 4], [1, 2, 3, 4, 5]]
Now I want to check whether this lists is in Av($\pi_1,\pi_2$) , the permutations that avoid the two permutations $\pi_1$ and $\pi_2$ when $\pi_1$ and $\pi_2$ are given (or maybe even more than two given permutations).
Is there an easy or even existing way to do this with Sage?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">klaaa</dc:creator><pubDate>Sat, 14 Aug 2021 21:21:40 +0200</pubDate><guid>https://ask.sagemath.org/question/58461/</guid></item><item><title>Convert between different ways of expressing permutations</title><link>https://ask.sagemath.org/question/51663/convert-between-different-ways-of-expressing-permutations/</link><description> Suppose I have two permutations x and y, given in one line notation (e.g. x=[2,1,4,3] and y=[3,2,1,4]). How would I go about computing e.g. the Kazhdan-Lusztig polynomial P<sub>x,y</sub>(q) in sage? The KL polynomial requires as input representing symmetric group elements as products of simple reflections and I do not know how to (using a computer) convert between these different ways of expressing a permutation. How does one do this in sage?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Peter M</dc:creator><pubDate>Mon, 01 Jun 2020 00:56:29 +0200</pubDate><guid>https://ask.sagemath.org/question/51663/</guid></item><item><title>How to make a permutation of a card problem and compute its order?</title><link>https://ask.sagemath.org/question/50468/how-to-make-a-permutation-of-a-card-problem-and-compute-its-order/</link><description> Risto arranged card deck cards first by suits and when by numerical values. After that he started to deal cards to piles such that every pile contained equal number of cards. As he had no cards, he collected the piles and started to deal the deck in the similar process. It took time but Risto continued doealing. Suddenly the cards were on their original order.
Task
Program knows the number of cards, number of piles, and the number of cards to be put on every pile. The task is to compute how many times Risto must collect the cards such that the cards are on their original order.
Cards have been dealt one at time and the cards have been put one the piles on the same order. As one has dealt every card, piles are gathered together such that the first pile goes to the most bottom in the pile. After that the cards in the new order will be piled and combined ia a similar way. Finally the order of cards will be as in the start.
In the next picture one can see a process if there are four cards and two piles. In the first pine one always adds two cards and on the second pile one adds one card. In this case a pile contains three cards and on the second deal there remains only one card that goes to the first pile.
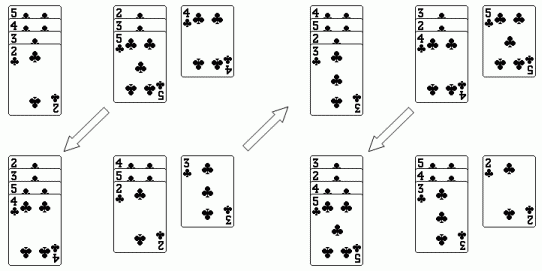
After four arrangements the order of the cards is as in the beginning. This means it takes four rounds to get cards to their original order.
How can I solve the problem by computer if the data of cards are as in https://www.ohjelmointiputka.net/tiedostot/korkie.txt ? The first number is the number of cards, then the number of piles and the next the number of cards one adds to every pile.
The format of the answer
Every line contains
- number of cards
- number of rounds to get cards into the original order.
For example, the answer to the example is
4 4
I think one could make some kind of permutation and compute its order. But how can I implement it?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">mathhobbyist</dc:creator><pubDate>Thu, 02 Apr 2020 17:50:59 +0200</pubDate><guid>https://ask.sagemath.org/question/50468/</guid></item><item><title>Orbits on group actions acting on sets</title><link>https://ask.sagemath.org/question/9652/orbits-on-group-actions-acting-on-sets/</link><description>Hello!
I am wondering how to solve the following problem efficiently.
I have a Permuation Group $G$ acting on $A = \{1,\ldots,n\}$ and I wish to compute the orbits of $G$ but not the ones of $G$ acting on $A$ but rather for $G$ acting on some $S \subseteq A \times A$ in the natural way. That is if $g \in G$ and $ x = \{a,b\} \in S$ then $x^g = {a^g,b^g\} \in S$
Other software for permuation groups (magma, gap) allows to do this by specifing an additional option "on sets/on tuples" to compute the specifed orbits.
I am wondering how could I do the same in sage, given a permuation group $G$ and an $S$ as described above.
Thanks!</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">SGQ</dc:creator><pubDate>Wed, 26 Dec 2012 10:56:11 +0100</pubDate><guid>https://ask.sagemath.org/question/9652/</guid></item><item><title>Determining if two subgroups of a symmetric group are conjugate</title><link>https://ask.sagemath.org/question/44357/determining-if-two-subgroups-of-a-symmetric-group-are-conjugate/</link><description>If I have two particular subgroups of a symmetric group, is there any built-in way in Sage to determine if the groups are conjugate to one another? I tried creating a `ConjugacyClass` for each and then comparing them, but this gives an error:
S = SymmetricGroup(3)
gen1 = Permutation('(1,2,3)')
gen2 = Permutation('(1,3,2)')
gen3 = Permutation('(1,2)')
gen4 = Permutation('(1,3)')
G1 = PermutationGroup([gen1, gen3])
G2 = PermutationGroup([gen2, gen4])
ConjugacyClass(S, G1) == ConjugacyClass(S, G2)
When executing the very last line I get the error
TypeError: For implementing multiplication, provide the method '_mul_' for (1,2) resp. Permutation Group with generators [(1,2), (1,2,3)]
</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">cjohnson</dc:creator><pubDate>Tue, 20 Nov 2018 20:06:56 +0100</pubDate><guid>https://ask.sagemath.org/question/44357/</guid></item><item><title>Is there any code to calculate the subgroup generated by the permutations</title><link>https://ask.sagemath.org/question/47371/is-there-any-code-to-calculate-the-subgroup-generated-by-the-permutations/</link><description> Consider the Symmetric Group $S_4$
I have three permutations namely $(3,4), (1,2), (1,3)(2,4)$.
How to find the subgroup generated by these permutations ?
Is there any code to calculate in Sagemath the subgroup generated by the permutations given above?
As an example the code should work like this :
If I input $(12)$ the code should give $\{(12),e\}$
Can someone help please?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Captcha</dc:creator><pubDate>Sun, 04 Aug 2019 08:16:11 +0200</pubDate><guid>https://ask.sagemath.org/question/47371/</guid></item><item><title>Constructing graphs using permutation or symmetric groups</title><link>https://ask.sagemath.org/question/46450/constructing-graphs-using-permutation-or-symmetric-groups/</link><description> I'm trying to construct a graph whose vertices are the elements of a permutation group or a symmetric group. Whenever I do this, it ignores the identity element (). For instance, when I use the Symmetric Group S3, it prints a graph with 5 vertices and the missing vertex is the identity.
Any ideas on why this happening and how I can fix it? </description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">homiermorphism</dc:creator><pubDate>Sat, 04 May 2019 22:47:42 +0200</pubDate><guid>https://ask.sagemath.org/question/46450/</guid></item><item><title>Obtaining integers from a linear extension of a poset.</title><link>https://ask.sagemath.org/question/45668/obtaining-integers-from-a-linear-extension-of-a-poset/</link><description>I'm quite new to Sage so this might be a very easy question.
Suppose that I have defined a linear extension of a poset in Sage like this:
P = Poset(([1,2,3,4], [[1,3],[1,4],[2,3]]), linear_extension=True, facade=False)
p = P.linear_extension([1,4,2,3])
Is there a way for me to make this linear extension into a permutation? That is, I would like to obtain the permutation [1,4,2,3] from p.</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">joakim_uhlin</dc:creator><pubDate>Tue, 05 Mar 2019 16:21:13 +0100</pubDate><guid>https://ask.sagemath.org/question/45668/</guid></item><item><title>does as_permutation_group() respect generators?</title><link>https://ask.sagemath.org/question/40927/does-as_permutation_group-respect-generators/</link><description>From sage documentation I can construct a group as follows:
sage: m1 = matrix(GF(11), [[1,2],[3,4]])
sage: m2 = matrix(GF(11), [[1,3],[10,0]])
sage: G = MatrixGroup(m1, m2); G
Matrix group over Finite Field of size 11 with 2 generators (
[1 2] [ 1 3]
[3 4], [10 0]
)
Now I use the following code:
sage: G_p=G.as_permutation_group(); G_p
Permutation Group with generators [(1,2,3,4,5,6,7,8,9,10,11)(12,13,15,14,16)(17,18), (1,3,5,7,9,11,2,4,6,8,10)(12,14,13,16,15)(17,18)]
In this case it is true that the generators of G are in correspondence with the generators of G_p. Is this always the case? I mean, if I compute a very complicated group G with lots of generators and its corresponding permutation group G_p, then is it true that G.gens()[i] corresponds to G_p.gens[i]?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">amontero90</dc:creator><pubDate>Thu, 01 Feb 2018 20:20:47 +0100</pubDate><guid>https://ask.sagemath.org/question/40927/</guid></item><item><title>Matrix Permutations</title><link>https://ask.sagemath.org/question/40180/matrix-permutations/</link><description> Hello,
how do I get all permutations of a Matrix?
For the following exercise I would like to get all permutations of a Matrix with integer values in the range $0$ to $9$. There should be $10^4$ permutations. And then generate the permutations of tuples with three matrices. $10^{12}$ permutations and then I would filter the list somehow for the invertible matrices.
Is there a better way?
Exercise:
Let $S, T, U \in \mathbb{R}^{2x2}$ such that, $S_{i, j}, T_{i, j}, U_{i, j} \in \{0,1, \cdots, 9\}$
How many of the products $S \cdot T \cdot U$ are invertible?
In the Sage reference for permutation I couldn't find any thing.
Thanks
PS: The curly braces couldn't be escaped properly in the LaTex part ... \\{0,1, \cdots, 9\\}</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Asg</dc:creator><pubDate>Fri, 15 Dec 2017 18:34:07 +0100</pubDate><guid>https://ask.sagemath.org/question/40180/</guid></item><item><title>permutations with property</title><link>https://ask.sagemath.org/question/37155/permutations-with-property/</link><description> How can I get a list of permutations $\sigma \in \mathfrak{S}_n$ with the property that $\sigma(i) \geq i-1$ for all $i =1, dots, n.$</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Ahmed</dc:creator><pubDate>Mon, 03 Apr 2017 22:41:41 +0200</pubDate><guid>https://ask.sagemath.org/question/37155/</guid></item><item><title>Changing a 1-line permutation to a string 'blablabla'</title><link>https://ask.sagemath.org/question/36828/changing-a-1-line-permutation-to-a-string-blablabla/</link><description> Hello, guys. First of all I'm very new to Sage, and also this forum, so please be generous to my question..
So, I was wondering given a permutation, say
Permutation([1,2,3,4])
how can I change to a string of the form
'1234'
??
Thank you for any help.</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">sssageeee</dc:creator><pubDate>Sat, 04 Mar 2017 20:40:53 +0100</pubDate><guid>https://ask.sagemath.org/question/36828/</guid></item><item><title>Transposing a Permutatoin</title><link>https://ask.sagemath.org/question/32498/transposing-a-permutatoin/</link><description> So I'm trying to take a permutation from a subgroup and add 5 to every digit in the permutation. For example if G=SymmetricGroup[5], G[2]=(1,2,3,4,5) , then I want the symmetric group isomorphic to G but where the 2nd element is (6,7,8,9,10). I also want to do this for arbitrary permutation groups, not just the symmetric groups.</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">kvissuet</dc:creator><pubDate>Mon, 08 Feb 2016 17:09:50 +0100</pubDate><guid>https://ask.sagemath.org/question/32498/</guid></item><item><title>Need to shift a permutation (1,2,3)(4,5)->(6,7,8)(9,10)</title><link>https://ask.sagemath.org/question/32499/need-to-shift-a-permutation-12345-678910/</link><description>So I've been trying to shift a permutation group upwards to be able to make a cartesian product of two arbitrary permutation groups into a permutation group. My idea was to simply shift one permutation group up enough so that it commutes with the other. However I am stuck trying to figure out how to shift it up, i.e. add 5 to each number in the permutation. Anyone have any ideas?
Thanks</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">kvissuet</dc:creator><pubDate>Mon, 08 Feb 2016 17:25:37 +0100</pubDate><guid>https://ask.sagemath.org/question/32499/</guid></item><item><title>Counting cycles of induced permutations</title><link>https://ask.sagemath.org/question/31888/counting-cycles-of-induced-permutations/</link><description>In order to do some sophisticated counting in graph theory, I need to count the cycles of some particular permutations.
In my situation, $n$ is an integer greater than 1, and $K_n$ is the set of all two-element sets {a,b} with $a, b$ being integers not greater than $n$. Now any element $\pi$ of the symmetric group $S_n$ induces a permutation $\overline{\pi}$ of $K_n$ in a natural way, i.e. $\overline{\pi}$ maps any set {a,b} of $K_n$ onto {$\pi(a)$, $\pi(b)$}. What I want to figure out with the help of SAGE is the number of cycles that the permutation $\overline{\pi}$ has.
If you can help me, please do not forget to mention those little extra things that need to be done and that might appear obvious to you (e.g. importing packages and so forth), since I am a relative novice to SAGE.
Thank you very much.
Malte</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Malte</dc:creator><pubDate>Mon, 28 Dec 2015 17:56:15 +0100</pubDate><guid>https://ask.sagemath.org/question/31888/</guid></item><item><title>the permutation of subscripts of a multivariate polynomial</title><link>https://ask.sagemath.org/question/23385/the-permutation-of-subscripts-of-a-multivariate-polynomial/</link><description> I want to define a function, the input are a permutation sigma belonging to Sn, and a multivariate polynomial f=f(x1,x2,...,xn) over Q, and the output is a multivariate polynomial f=f(x(sigma(1)),x(sigma(2)),...,x(sigma(n))),
for example, if sigma=(3,1,2),f=x1+x2*x3, then the output should be f=x3+x1*x2.
It is worth mentioning that this should work for any n not just when n=3.
How should I do that?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">ruidongshuai@gmail.com</dc:creator><pubDate>Sat, 12 Jul 2014 16:32:22 +0200</pubDate><guid>https://ask.sagemath.org/question/23385/</guid></item><item><title>Permutations indexed from zero</title><link>https://ask.sagemath.org/question/23402/permutations-indexed-from-zero/</link><description>Is there an option to have permutations indexed from zero instead of one, in other words can we have permutations on the integers 0 to n-1 instead of permutations on the integers 1 to n. This would be useful since indexation for lists, tuples, and iterables in general is usually from zero. Indices for variable names of generators of various algebraic structures, such as multivariate polynomial rings, finitely presented groups, etc., also start from zero.
I saw that `PermutationOptions` lets you choose how to display permutations, and whether to multiply them from left to right or right to left, but found nothing about having indices starting from zero versus one.
</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">slelievre</dc:creator><pubDate>Sun, 13 Jul 2014 19:10:27 +0200</pubDate><guid>https://ask.sagemath.org/question/23402/</guid></item></channel></rss>