<?xml version="1.0" encoding="utf-8"?>
<rss xmlns:atom="http://www.w3.org/2005/Atom" version="2.0"><channel><title>ASKSAGE: Sage Q&A Forum - RSS feed</title><link>https://ask.sagemath.org/questions/</link><description>Q&A Forum for Sage</description><atom:link href="https://ask.sagemath.org/feeds/rss/" rel="self"></atom:link><language>en</language><copyright>Copyright Sage, 2010. Some rights reserved under creative commons license.</copyright><lastBuildDate>Tue, 13 May 2025 01:16:32 +0200</lastBuildDate><item><title>Output of RootedTrees()</title><link>https://ask.sagemath.org/question/82781/output-of-rootedtrees/</link><description>Dear all,
I’m currently working on rooted trees and I wanted to ask if there is an alternative output for rooted trees by using HashTables or edge sets.
For example, if I run the following code:
n = 5
trees = RootedTrees(n)
for T in trees:
print(T)
The output I get is:
[[[[[]]]]]
[[[[], []]]]
[[[], [[]]]]
[[[], [], []]]
[[], [[[]]]]
[[], [[], []]]
[[[]], [[]]]
[[], [], [[]]]
[[], [], [], []]
**Is there a different way to represent or obtain this output using HashTables or edge sets?** For instance, I guess [[], [], [], []] means the tree G having E(G)={{1,2},{1,3},{1,4},{1,5}}</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Hola</dc:creator><pubDate>Tue, 13 May 2025 01:16:32 +0200</pubDate><guid>https://ask.sagemath.org/question/82781/</guid></item><item><title>Problems with memory usage with bliss algorithm</title><link>https://ask.sagemath.org/question/72676/problems-with-memory-usage-with-bliss-algorithm/</link><description>I am trying to run a very long (weeks long) process that constructs a large collection of graphs.
The collection is too large to keep in memory and so as each graph is found it is stored on disk (rather than in an array).
However when I set it running, I noticed that the amount of RAM used by the process was continuously increasing until the rest of the machine ground to a halt. My computer has 64Gb RAM and it takes a bit more than a day for the process to grow to that size.
I have tried to isolate the part of the program that was causing the memory usage to grow, and I think that I have isolated it to the canonical labelling algorithm "bliss".
Here is a simple program that just creates random graphs and canonically labels them (but does nothing more):
for it in range(1000000):
g = graphs.RandomGNP(20,0.5)
gc = g.canonical_label(algorithm="bliss")
if it % 1000 == 0:
print(it)
When I run this program the memory consumed grows and grows.
If I change the program to use the built-in Sage method,
for it in range(1000000):
g = graphs.RandomGNP(20,0.5)
gc = g.canonical_label(algorithm="sage")
if it % 1000 == 0:
print(it)
then the program runs to completion with no increase in memory used - the memory is correctly being recovered as it goes out of scope each time through the loop.
What should I do in this situation?
</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Gordon</dc:creator><pubDate>Fri, 18 Aug 2023 04:24:53 +0200</pubDate><guid>https://ask.sagemath.org/question/72676/</guid></item><item><title>Some "strange behaviors“ of longest_path</title><link>https://ask.sagemath.org/question/69746/some-strange-behaviors-of-longest_path/</link><description>**version:** Sage 10.
I want to find a longest path starting from a given vertex in a graph. Below is my graph, and I have observed that if the longest path starting from a given vertex is a Hamiltonian path, `longest_path` responds very quickly. However, if it is not a Hamiltonian path, the response time is slow.
g1=Graph({0: [2, 3, 4, 15], 1: [16, 2, 3, 15], 2: [0, 1, 3, 4], 3: [0, 1, 2, 4], 4: [0, 2, 3, 15], 5: [7, 8, 9, 14], 6: [16, 7, 8, 9], 7: [5, 6, 8, 9], 8: [5, 6, 7, 9], 9: [5, 6, 7, 8], 10: [11, 12, 13, 14], 11: [16, 10, 12, 13], 12: [10, 11, 13, 14], 13: [16, 10, 11, 12], 14: [5, 10, 12, 15], 15: [0, 1, 4, 14], 16: [1, 6, 11, 13]})
Here is the calculation process.
g1.longest_path(1) # quckily
g1.longest_path(14) # long time, about 100s
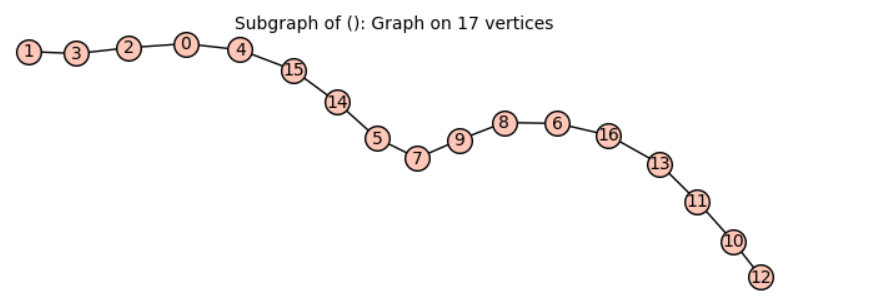
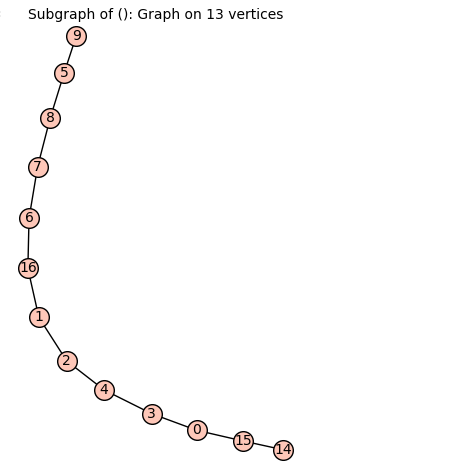
Additionally, I have noticed that the option **backtracking** in `longest_path`does not seem to work when we specify the starting vertex. Looking at the output below, it is 1 or 9, not the longest path starting from vertex 14.
g1.longest_path(14,algorithm="backtrack")

**Question 1.** Why is there such a significant difference between the two cases?( When a vertex is given and there exists a Hamiltonian path that contains it as the starting vertex, it is puzzling why it is found quickly, while non-Hamiltonian paths take much longer.)
**Question 2.** Does the backtracking method not work when a starting vertex is given?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">licheng</dc:creator><pubDate>Thu, 06 Jul 2023 04:37:51 +0200</pubDate><guid>https://ask.sagemath.org/question/69746/</guid></item><item><title>Edge isoperimetric number</title><link>https://ask.sagemath.org/question/52410/edge-isoperimetric-number/</link><description>This is probably a very silly question. How does one get the edge isoperimetric number of a graph?
As seen under [here](https://trac.sagemath.org/ticket/21942) there should be an algorithm for it, but when I define a graph (say H), then
<code>
edge_isoperimetric_number(H)
</code>
returns "name 'edge_isoperimetric_number' is not defined"
and
<code>
H.edge_isoperimetric_number()
</code>
returns "'Graph' object has no attribute 'edge_isoperimetric_number'"
(while
<code>
edge_isoperimetric_number?
</code>
returns "Object `edge_isoperimetric_number` not found."
So how do I load said algorithm for use?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">ARG</dc:creator><pubDate>Fri, 10 Jul 2020 22:04:04 +0200</pubDate><guid>https://ask.sagemath.org/question/52410/</guid></item><item><title>fractional chromatic index of edge-weighted graphs</title><link>https://ask.sagemath.org/question/46900/fractional-chromatic-index-of-edge-weighted-graphs/</link><description>How would you compute the fractional chromatic index of an edge-weighted graph using SAGE?
The built-in function fractional_chromatic_index seems to compute the fractional chromatic index for only unweighted graphs. For instance, if $G$ is the 5-cycle graph, its fractional chromatic index is $2.5$. But if one of the edges can be ignored, say by giving it a zero weight, then the fractional chromatic index becomes $2$.
The code and output below shows that SAGE ignores the edge-weights (notice that the edge-weights need not be integral - in the graph below, the correct value of the fractional chromatic index is 2.1, which is the maximum sum $1.1+1.0$ of weights of edges incident to a vertex):
sage: G = graphs.EmptyGraph()
sage: G.add_edges([(1,2,1.1),(2,3,1),(3,4,1),(4,5,1),(5,1,0)])
sage: G.fractional_chromatic_index()
5/2
sage:
Is there some way to get the built-in function to take edge weights into account? Or can this value be computed using some other method?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Ashwin Ganesan</dc:creator><pubDate>Tue, 11 Jun 2019 10:52:15 +0200</pubDate><guid>https://ask.sagemath.org/question/46900/</guid></item><item><title>Way to solve max_split enumeration</title><link>https://ask.sagemath.org/question/38283/way-to-solve-max_split-enumeration/</link><description>Hello everyone,
I try to solve a problem on graphs. The graphs contain two types of nodes, a first type linked together containing max_cliques that I seek to determine. A second one connected only to the first.
For the moment I enumerate the biggest cliques of the first type, then determines for each the number of nodes of the second type related to this one. Finally I list the one with the largest number of nodes of the second type.
So I'm looking to find the biggest split graph.
Do you have an idea to improve my current way?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">AlexJ</dc:creator><pubDate>Sun, 16 Jul 2017 12:32:13 +0200</pubDate><guid>https://ask.sagemath.org/question/38283/</guid></item><item><title>multi commodity algorithm reference</title><link>https://ask.sagemath.org/question/37028/multi-commodity-algorithm-reference/</link><description> Hello,
I'm using "multicommodity_flow()" method for my research and I really like to know what is the reference for the solution used in the code, like a publication, book or article.
Thanks,
Amir</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Amir19</dc:creator><pubDate>Wed, 22 Mar 2017 09:09:04 +0100</pubDate><guid>https://ask.sagemath.org/question/37028/</guid></item><item><title>Multi-Commodity Flow problem, solution reference</title><link>https://ask.sagemath.org/question/37029/multi-commodity-flow-problem-solution-reference/</link><description> Hello,
I am using "multicommodity_flow()" method for my research and I would like to know the reference behind the solution, like a paper, book or an article.
Thanks,
Amir</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Amir19</dc:creator><pubDate>Wed, 22 Mar 2017 09:12:08 +0100</pubDate><guid>https://ask.sagemath.org/question/37029/</guid></item><item><title>Recursive Algorithm for Graph Coloring</title><link>https://ask.sagemath.org/question/34051/recursive-algorithm-for-graph-coloring/</link><description>In a 2014 article by Exoo, Ismailescu, and Lim ("On the Chromatic Number of R^4"), a recursive algorithm is described that verifies the absence of a proper $k$-coloring of a graph $G$. The authors include only the following description of the algorithm.
"[The program is] based on the following recursive procedure that does an exhaustive search for a $K$-coloring of a graph of order $N$. It employs a global variable *color*, an array of order $N$, which records the color of each vertex $v$ for $1 \leq v \leq N$. The search is initiated with the call DFS(1)."
procedure DFS(v):
Local variable: FCSet - the set of feasible colors for vertex v.
if v > N:
All vertices have been colored, report G is K-colorable.
Exit.
end if
FCSet = {1 ... K}
for u = 1 to v-1:
if u is adjacent to v:
FCSet = FCSet - color(u)
end if
end for
for c in FCSet:
color(v) = c
DFS(v+1)
end for
end procedure
I am having difficulty implementing this algorithm in Sage. Given the nature of the program, I thought Java would be a more natural programming language to use for this algorithm, but I'm afraid I am not familiar with Java syntax.
Any help with implementing this algorithm would be greatly appreciated! </description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">JEA</dc:creator><pubDate>Thu, 07 Jul 2016 19:53:25 +0200</pubDate><guid>https://ask.sagemath.org/question/34051/</guid></item><item><title>Dotted and dashed lines in directed graphs</title><link>https://ask.sagemath.org/question/31304/dotted-and-dashed-lines-in-directed-graphs/</link><description>Hi,
I would like to know if it is possible to do (one of) the following with Sage.
Reading
http://doc.sagemath.org/html/en/reference/plotting/sage/graphs/graph_plot.html
I saw that it is possible to draw dashed and dotted lines. Now my questions are
1) Is it possible to produce an output graphic where some edges are dotted and some edges are dashed?
2) Is it possible to force the text in the labels of the vertices, e.g. M2, M4, M1 instead of 0,1,2?
Thanks for the help!
</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Bern</dc:creator><pubDate>Fri, 04 Dec 2015 03:39:18 +0100</pubDate><guid>https://ask.sagemath.org/question/31304/</guid></item></channel></rss>