<?xml version="1.0" encoding="utf-8"?>
<rss xmlns:atom="http://www.w3.org/2005/Atom" version="2.0"><channel><title>ASKSAGE: Sage Q&A Forum - RSS feed</title><link>https://ask.sagemath.org/questions/</link><description>Q&A Forum for Sage</description><atom:link href="https://ask.sagemath.org/feeds/rss/" rel="self"></atom:link><language>en</language><copyright>Copyright Sage, 2010. Some rights reserved under creative commons license.</copyright><lastBuildDate>Thu, 02 May 2024 17:34:30 +0200</lastBuildDate><item><title>contour_plot behaves differently when I include the functional dependence</title><link>https://ask.sagemath.org/question/77204/contour_plot-behaves-differently-when-i-include-the-functional-dependence/</link><description> If I include the functional dependence of my function, the contour_plot routine behaves differently. MWE:
var('x y')
def check(x,y):
val=-1. # negative by default,
for j in range(1,10):
for i in range(1,10):
if ( ( (x>0.9*i) and (x<1.1*i) ) and ( (y>0.9*j) and (y<1.1*j) ) ):
val=1.
return val
So this is kind of a strange function, but basically if (x,y) are near any of the 2d grid points (1-10), the function is 1 instead of zero. If I call this function without specifying the functional dependence, it looks right:
contour_plot(check,(x,-1.,8.),(y,-1.,8.))
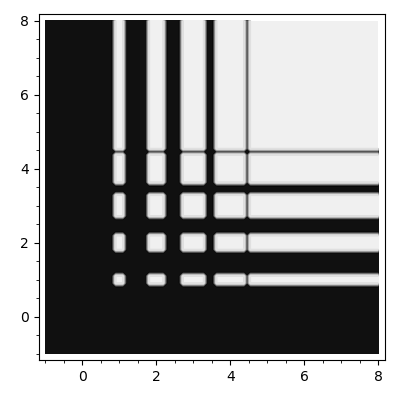
However, if I call them and specify them explicitly, I get the unexpected (to me):
contour_plot(check(x,y),(x,-1.,8.),(y,-1.,8.))
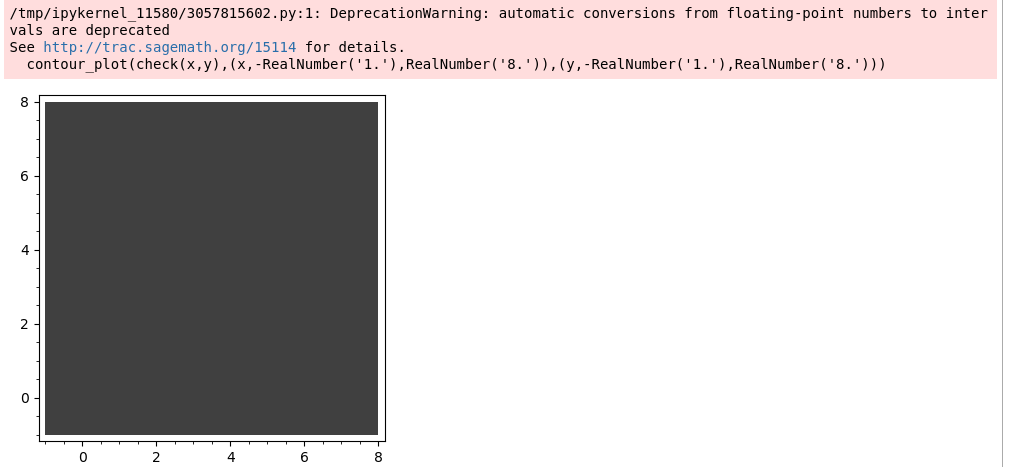
(I grabbed the depreciation warning too, although I don't see how it matters here).
This is not just academic, because what I really want to do is have a four-variable funcftion, a la
def h(x,y,z,w):
...
and do a contour plot on two variables, setting the other two constant, like
contour_plot(h(x,y,0,1),....)
I'm having trouble, and trying to debug. Any thoughts?
</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">thethinker</dc:creator><pubDate>Thu, 02 May 2024 17:34:30 +0200</pubDate><guid>https://ask.sagemath.org/question/77204/</guid></item><item><title>Contour Plot of 1/(2*pi*sqrt(x^2 + y^2)), why is it square? How to fix it?</title><link>https://ask.sagemath.org/question/61288/contour-plot-of-12pisqrtx2-y2-why-is-it-square-how-to-fix-it/</link><description>I plotted the contour plot of a function `1/(2*pi*sqrt(x^2 + y^2))`.
The code is below:
contour_plot(1/2/(pi*sqrt(x^2 + y^2)), (x, -0.1, 0.1), (y, -0.1, 0.1),
plot_points=20, colorbar=True)
**The output result is not round, but square! Why?**
**How to fix it?**</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Tube777tube</dc:creator><pubDate>Sat, 26 Feb 2022 15:44:14 +0100</pubDate><guid>https://ask.sagemath.org/question/61288/</guid></item><item><title>enriched contour plot</title><link>https://ask.sagemath.org/question/58365/enriched-contour-plot/</link><description>He there,
I would like to make a contour plot for a function of two variables that is enriched with the critical points of the function. I can plot each of the graphical objects separately, but when I try to combine them, something goes wrong, looks like the contour plot will always be at the top layer, this hidding the points.
Here is the code I am using (by the way, if somone has better ide to restrict the domain of the plot, that would be nice).
var('x,y')
def f(x,y):
if (x^2 + y^2 <= 1.01) :
return (x+y)*exp(-x^2 -y^2)
C = contour_plot(f ,(-1,1), (-1,1), cmap = "Spectral", labels = True, label_fmt=lambda x: "$%s$"%round(x,1), contours = 10, label_colors="black", label_inline=True, label_fontsize=10, fill = True, axes = True, axes_labels=["$x$","$y$"], axes_labels_size=1.5, tick_formatter = "latex", fontsize= 10)
C += parametric_plot([cos(x), sin(x)], (x,0,2*pi), color = "grey", thickness = 1.5)
C += point([(-0.5,-0.5), (-1/sqrt(2), -1/sqrt(2)), (0.5,0.5), (1/sqrt(2), 1/sqrt(2)) ], size = 60, color = "black")
C
In another figure I made, I managed to circumvent the problem by putting a text with $\\bullet$... not very elegant. It's quite strange that one can add decorations like vectors or text on top of a contour_plot, but not points.
Kind regards,
JC</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">JC</dc:creator><pubDate>Sun, 08 Aug 2021 17:52:23 +0200</pubDate><guid>https://ask.sagemath.org/question/58365/</guid></item><item><title>Using base 10 exponent of a number as label in a contour plot</title><link>https://ask.sagemath.org/question/53631/using-base-10-exponent-of-a-number-as-label-in-a-contour-plot/</link><description> I am currently trying to improve the labelling of a contour plot. As contours I'm only using negative powers of ten, so I hope to have a simple LaTeX label of the form, say, 10^{-23}. My starting point was one of the examples at the help page for contour_plot (here was the link to the sage documentation). After various failed attempts with log(x, 10), I found in the question "Integer types and log()" (that would be question id(?) 28679/integer-types-and-log) an example using valuation(x,10). However, the results seem odd. Below the slightly simplified thing I try to plot.
var('x y')
rp = 6.77048070412999e-10*(x + sqrt(x^2-y^2*x^2))
sigma0 = 1.44008750449331e-18*(3*x + sqrt(9*x^2 - 8*y^2*x^2))^4/(8*(3*x^2 - 2*y^2*x^2 + x*sqrt(9*x^2 - 8*y^2*x^2)))
f(x,y) = (1.12469227142351e-70*y*x^2/(rp)^6*exp(-(rp)^2/(sqrt(y)*x*0.169262017603250))-1.65389403372211e-162*(sqrt(x^2-y*x^2))^3*sigma0*(x-2*sqrt(x^2-y*x^2))/(rp)^10)
contour_plot(f(x,y), (x,0,100), (y,0,1), contours=[0,1e-25,1e-24,1e-23,1e-22,1e-21,1e-20,1e-19],aspect_ratio='automatic',labels=True, label_fmt=lambda x: r'''$10^{-%s}$'''%(valuation(1/x,10)), fill=False)
If I do this, I get 10^{-0} for several contours.
So, I checked, what valuation does to the numbers:
print(valuation(1/(1e-19),10))
print(valuation(1/(1e-20),10))
print(valuation(1/(1e-21),10))
print(valuation(1/(1e-22),10))
print(valuation(1/(1e-23),10))
yielding
19
20
0
22
0
If I'm using something like
label_fmt=lambda x: r'''$10^{-%s}$'''%(log(1/x,10))
instead, I get only the message "Graphics object consisting of 1 graphics primitive", and
label_fmt=lambda x: r'''$10^{-%s}$'''%(log(Integer(1/x),10))
yields another plot with odd labels - which have the odd behaviour at the same exponents as the example with "valuation", but I don't know why.
I'm currently doing this mostly in a jupyter notebook on Windows 10 with Sage 9.1.
Am I misunderstanding the use of "valuation" or log(x,10) in this case? Did I run into a bug? How can I get the exponents I'm after?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Wraith-of-Seth</dc:creator><pubDate>Mon, 28 Sep 2020 08:00:42 +0200</pubDate><guid>https://ask.sagemath.org/question/53631/</guid></item><item><title>weird behavior of show command</title><link>https://ask.sagemath.org/question/48051/weird-behavior-of-show-command/</link><description> Hi The code
f(x,y)=x^3-x^2 + y^2;print f
g1 = contour_plot(f(x,y),(x,-2,2),(y,-2,2),contours=20,fill=False,cmap='spectral')
show(g1)
produces a plot with a hyperbolic point. On my computer, repeating this
show(g1)
yields a different plot
The purpose was to show this together with gradient field
f(x,y)=(x+2)^2/(y^2+ (x-1/2)^2) ;print f
g1 = contour_plot(f(x,y),(x,-2,6),(y,-2,4),contours=[1/10,1/2,4/5,1,2,3],cmap='spectral',fill=False)
df=f.gradient()
show(df)
g2 = plot_vector_field(df,(x,-2,2),(y,-2,2))
This doesn't work, since the first plot is incorrect
show(g1+g2)</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">florin</dc:creator><pubDate>Wed, 25 Sep 2019 10:34:10 +0200</pubDate><guid>https://ask.sagemath.org/question/48051/</guid></item><item><title>Graphing max function - unexpected behavior</title><link>https://ask.sagemath.org/question/43797/graphing-max-function-unexpected-behavior/</link><description> My minimal working example is:
(x,y) = var('x y')
def f(x,y):
return max(abs(x),abs(y))
table([[f(x,y) for y in range(-3,4)] for x in range(-3,4)])
The output is this table:
3 3 3 3 3 3 3
3 2 2 2 2 2 3
3 2 1 1 1 2 3
3 2 1 0 1 2 3
3 2 1 1 1 2 3
3 2 2 2 2 2 3
3 3 3 3 3 3 3
That looks like it ought to. But when I try
contour_plot(f(x,y),(x,-3,3),(y,-3,3))
I get something that looks a lot different. It seems I don't have enough karma to upload the image, but its looks more like the one that would be associated to this table:
table([[f(0,y) for y in range(-3,4)] for x in range(-3,4)])
3 2 1 0 1 2 3
3 2 1 0 1 2 3
3 2 1 0 1 2 3
3 2 1 0 1 2 3
3 2 1 0 1 2 3
3 2 1 0 1 2 3
3 2 1 0 1 2 3
I have the issue isolated in a Sage worksheet on CoCalc. I don't have enough karma to include a link, either.</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">leingang</dc:creator><pubDate>Sun, 30 Sep 2018 21:22:00 +0200</pubDate><guid>https://ask.sagemath.org/question/43797/</guid></item><item><title>3D Graph with Domain contours</title><link>https://ask.sagemath.org/question/43985/3d-graph-with-domain-contours/</link><description>Hi
I would like to visualize in 3D the function below:
f_{X,Y}(x,y) = \begin{array}{ll} x^2, & \mbox{if $1 \leq x \leq 2$ and $0 \leq y \leq x$}, \\ 0, & \mbox{otherwise}. \end{array} .
I execute this code below, but it is not displaying good (what is wrong with the code ?), and how to display the axes labels ?
var("x y z")
region = implicit_plot3d(z, (x, -3, 3), (y, -3, 3), (z, -3, 3) , plot_points=100, region=lambda x,y,z: x^2 and 1<x and x<2 and y<x and y>0,axes=True)
region.show()</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">ortollj</dc:creator><pubDate>Fri, 19 Oct 2018 12:40:34 +0200</pubDate><guid>https://ask.sagemath.org/question/43985/</guid></item><item><title>Fill colors with two contour plots</title><link>https://ask.sagemath.org/question/41457/fill-colors-with-two-contour-plots/</link><description>Assume I have two contour plots, of functions A and B, say, depending on x and y, with one level curve on each plot.
There are two different zones in each plot, filled with two colors, like in the following:
Gr=Graphics();
Gr += contour_plot(A,(x,0,10),(y,0,10),contours=1,cmap=['white', 'red']);
Gr += contour_plot(B,(x,0,10),(y,0,10),contours=1,cmap=['yellow', 'blue']);
show(Gr);
The problem is that the resulting picture only shows the filling colors of the second plot.
How do I get a picture with each zone (from both plots) in a different color ? some kind of transparency ?
Sorry if my question is trivial,
Thanks !</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">user111</dc:creator><pubDate>Fri, 09 Mar 2018 22:30:28 +0100</pubDate><guid>https://ask.sagemath.org/question/41457/</guid></item><item><title>Unable to create a contour_plot of a system of inequalities</title><link>https://ask.sagemath.org/question/34111/unable-to-create-a-contour_plot-of-a-system-of-inequalities/</link><description>I am trying to plot a system of inequalities, dependent on a matrix H. Here is my function I am planning to contour_plot: <br>
def reg(x, y):
f1 = H[0,0] * H[0,0] * x + H[1,0] * H[1,0] * y
f2 = H[0,0] * H[0,1] * x + H[1,0] * H[1,1] * y
f3 = H[0,1] * H[0,1] * x + H[1,1] * H[1,1] * y
if f1 < 0 or f2 < 0 or f3 < 0:
return 0
else:
return 1
I then have H be
> H
> [2.220446049250313e-16 -0.9999999999999998]
> [ -0.9999999999999998 2.220446049250313e-16]
However
contour_plot(reg, (x,-Integer(5),Integer(5)), (y,-Integer(5),Integer(5)))
yields an error. It says
zero-size array to reduction operation minimum which has no identity
The strange part is that when
> H
> [-1 0]
> [ 0 1]
the same contour_plot yields exactly what I want without any errors <br>
Help would be much appreciated, I have just picked up SAGE this week and have much to learn
</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">petkus</dc:creator><pubDate>Sat, 16 Jul 2016 21:30:45 +0200</pubDate><guid>https://ask.sagemath.org/question/34111/</guid></item><item><title>built in method norm of Vector_symbolic_dense object</title><link>https://ask.sagemath.org/question/25835/built-in-method-norm-of-vector_symbolic_dense-object/</link><description> So, I want to write a program that plots equipotential contours for z=0 for electric potential of 3 charges(ch) at specified coordinates(matrix m). I need rv to be a vector with general coordinates so I can later plot the equipotential contours.
var(' x y ')
m=matrix(QQ,[[1,1],[-1,-1],[-1,1]])
ch=([-1,1,1])
rv=vector([x,y])
k=m.nrows();
u=[(rv-m[i]).norm() for i in range(k)];
However, after the last line I get this:
[<built in method norm of Vector_symbolic_dense object at 0xbb752fc>, <built in method norm of Vector_symbolic_dense object at 0xbb7532c>, <built in method norm of Vector_symbolic_dense object at 0xbb750bc>]
How do I fix this to get the norm of rv-m[i]?
,</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">idonea</dc:creator><pubDate>Sun, 15 Feb 2015 22:22:21 +0100</pubDate><guid>https://ask.sagemath.org/question/25835/</guid></item><item><title>generate_plot_points for multiple variable functions and contour_plot</title><link>https://ask.sagemath.org/question/9140/generate_plot_points-for-multiple-variable-functions-and-contour_plot/</link><description>Is there a default sage function to generate all (x,y,f(x,y)) values the program uses to draw a multivariable function or the contours of let's say a f(x,y)=C ?
I am new to sage and could only find that generate_plot_points works only for one variable functions.
Example from documentation:
sage: from sage.plot.plot import generate_plot_points
sage: generate_plot_points(sin, (0, pi), plot_points=2, adaptive_recursion=0)
I guess one could solve symbolically let's say a contour equation and then create the values i talk about like discussed [here](https://groups.google.com/forum/?fromgroups#!topic/sage-devel/ax09DwbbnGo):
sage: var('x,y')
(x, y)
sage: solve(y^2 - x^3 - x == 0, [y])
[y == -sqrt(x)*sqrt(x^2 + 1), y == sqrt(x)*sqrt(x^2 + 1)]
then just plot each of those two above and combine them. But this could become really cumbersome since one could have a terribly complicated equation. So can this be done currently or someone needs a workaround to achieve this?
excuse my english :)
</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Cosmos</dc:creator><pubDate>Fri, 06 Jul 2012 14:54:10 +0200</pubDate><guid>https://ask.sagemath.org/question/9140/</guid></item><item><title>contour_plot issue with large numbers</title><link>https://ask.sagemath.org/question/10536/contour_plot-issue-with-large-numbers/</link><description>I was trying to whip up a variant on Tupper's "self-referential" formula graph (nice exposition [here](http://shreevatsa.wordpress.com/2011/04/12/how-does-tuppers-self-referential-formula-work/) if you're not familiar with it) in Sage, but I ran into a graphing issue with largish numbers. In an attempt to nail down the problem, I've tried to reduce this to a minimal case:
x,y = var('x,y')
def mod2(x): return floor(x)-2*floor(x/2)
def mod4(x): return floor(x)-4*floor(x/4)
N=2^53+1
contour_plot(mod2((N+floor(y/4)) / 2^(4*floor(x)+mod4(y))),(x,0,14),(y,0,4))
(I wrote the mod2/4 functions because I kept on running into issues with the % operator and type coercion.)
If you understand the idea behind the Tupper formula, then you know that the binary representation of N is basically a readout of the "pixels" of the eventual graph generated. Now, 2^53+1 is 1000...001 in binary, so there should be
TWO "pixels" lit.
But, when I actually execute the above code on my home computer or in the Sage Cloud, something funny happens. I get a graph where only ONE "pixel" is lit -- the one corresponding to the least significant bit of 2^53+1, which should be in the bottom left of the graph (i.e., near the origin) is mysteriously absent.
However, if you check for...
N=2^52+1
...the graph correctly shows two "pixels". So I first presumed this was some sort of floating point or rounding error. But if you actually check the values returned by the function being graphed, the returned values are always correct. For example, setting (x,y) to a value squarely within the "missing pixel" and manually evaluating...
x,y=0.5,0.5
mod2((N+floor(y/4)) / 2^(4*floor(x)+mod4(y)))
...yields the correct value of 1, even for N=2^53+1! Similarly, setting (x,y) to (0.5,1.5), i.e., outside said "pixel", appropriately yields 0. So I don't get at all why the graphing isn't working.
Any insight would be appreciated.</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">sappidus</dc:creator><pubDate>Fri, 13 Sep 2013 15:25:34 +0200</pubDate><guid>https://ask.sagemath.org/question/10536/</guid></item><item><title>Contour plots</title><link>https://ask.sagemath.org/question/9885/contour-plots/</link><description>I plotted the vector field like this
p3= plot_vector_field( ((x+4)/sqrt((x+4)^2+y^2)+(x-6)/sqrt((x-6)^2+y^2), y/sqrt((x+4)^2+y^2)), (x, -10, 10), (y, -10, 10))
I would like to do a contour plot where contour joind points at the same value. How do I do that?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">nerak99</dc:creator><pubDate>Tue, 23 Apr 2013 05:01:27 +0200</pubDate><guid>https://ask.sagemath.org/question/9885/</guid></item><item><title>Colorbar for density plots</title><link>https://ask.sagemath.org/question/9460/colorbar-for-density-plots/</link><description>Hi!
I would like to know if there is a way to get a colorbar for a density plot. For contour plots this works fine with the colorbar=True option, but for density plots there doesn't seem to be such an option. Can anyone help?
Greetings,
Melvin</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">MelvinSmith</dc:creator><pubDate>Tue, 23 Oct 2012 20:57:25 +0200</pubDate><guid>https://ask.sagemath.org/question/9460/</guid></item><item><title>Piece-wise functions and plotting</title><link>https://ask.sagemath.org/question/9377/piece-wise-functions-and-plotting/</link><description>Hi,
I have a piece-wise defined function that I want to plot (and potentially do other symbolic stuff with) and I was wondering how to do this. The problem is that I am defining my function as a Python function:
<pre>def F(x,y):
if( x <= y ):
return x*y
return x+y
</pre>
So I am gluing together two pieces, and I would like to be able to do
<pre>(x,y) = var('x,y')
contour_plot( F(x,y), (x,0,1), (y,0,1) )</pre>
But the problem is that this only plots the second part. This occurs because x <= y evaluates as false (they are variables) and F(x,y) is always evaluated as x+y. In Mathematica there is the <b>Which</b> function that works on symbolic expression to make piece-wise definitions. Is there an equivalent in Sage? Is there another way to do this? If I had a function (say, <i>delta</i>) that just evaluated as 1 if the symbolic expression was true, and 0 if not, I could craft the function as:
<pre>F(x,y) = delta( x<=y ) * (x*y) + delta( x>y ) * (x+y)</pre>
But as it is, I think there is no way to do this. Is there?
Thanks a lot for your help,
Edgar</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Edgar</dc:creator><pubDate>Tue, 02 Oct 2012 11:20:42 +0200</pubDate><guid>https://ask.sagemath.org/question/9377/</guid></item><item><title>3d contour plotting in sage</title><link>https://ask.sagemath.org/question/9081/3d-contour-plotting-in-sage/</link><description>It seems there isn't a function in sagemath which can plot contours of a function
$f(x, y, z)$ as transparent layers in 3d space like in [mayavi](http://docs.enthought.com/mayavi/mayavi/auto/mlab_helper_functions.html#mayavi.mlab.contour3d).
Is there an alternate way to achieve the same effect in sage?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">ebs</dc:creator><pubDate>Sat, 16 Jun 2012 08:09:27 +0200</pubDate><guid>https://ask.sagemath.org/question/9081/</guid></item><item><title>contour plot not working as expected</title><link>https://ask.sagemath.org/question/8958/contour-plot-not-working-as-expected/</link><description>Hi all,
I am looking at ways to determine the sign of an angle between a reference vector (a,b) and any other vector(x,y) of the plane. To do so, I have decided to use the determinant of the matrix: [[a b],[x y]] which equals ax-by.
I wanted then to check that the formula works by displaying the plane area which positive and negative signs using the contour_plot.
Here is my question:
Why is the 3rd graph not showing 2 horizontal areas instead of the vertical displayed?
var('x y')
f(x,y,a,b)=(a*y-b*x)/abs(a*y-b*x)
plota1b1=contour_plot(f(x,y,1,1),(-10,10),(-10,10),cmap='jet',colorbar=true)
plota0b1=contour_plot(f(x,y,0,1),(-10,10),(-10,10),cmap='jet',colorbar=true)
plota1b0=contour_plot(f(x,y,1,0),(-10,10),(-10,10),cmap='jet',colorbar=true)
show(plota1b1)
show(plota0b1)
show(plota1b0)
Thanks
</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">sagemb</dc:creator><pubDate>Mon, 07 May 2012 04:34:12 +0200</pubDate><guid>https://ask.sagemath.org/question/8958/</guid></item><item><title>TypeError doing a contour plot of imag_part(I*log(x+I*y))</title><link>https://ask.sagemath.org/question/7500/typeerror-doing-a-contour-plot-of-imag_partilogxiy/</link><description>Hi. I'm trying to do a contour plot of the imaginary part of i*log(z).
z = var("z")
x,y = var("x,y",domain="real")
u = I*log(z)
f = imag_part(u(z=(x+I*y)))
contour_plot(f,(x,-3,3),(y,-3,3))
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
File "_sage_input_30.py", line 10, in <module>
exec compile(u'open("___code___.py","w").write("# -*- coding: utf-8 -*-\\n" + _support_.preparse_worksheet_cell(base64.b64decode("eiA9IHZhcigieiIpCngseSA9IHZhcigieCx5Iixkb21haW49InJlYWwiKQp1ID0gSSpsb2coeikKZiA9IGltYWdfcGFydCh1KHo9KHgrSSp5KSkpCmNvbnRvdXJfcGxvdChmLCh4LC0zLDMpLCh5LC0zLDMpKQ=="),globals())+"\\n"); execfile(os.path.abspath("___code___.py"))
File "", line 1, in <module>
File "/tmp/tmpk8YRSf/___code___.py", line 7, in <module>
exec compile(u'contour_plot(f,(x,-_sage_const_3 ,_sage_const_3 ),(y,-_sage_const_3 ,_sage_const_3 ))
File "", line 1, in <module>
File "/cosas/sage/local/lib/python2.6/site-packages/sage/misc/decorators.py", line 456, in wrapper
return func(*args, **kwds)
File "/cosas/sage/local/lib/python2.6/site-packages/sage/misc/decorators.py", line 456, in wrapper
return func(*args, **kwds)
File "/cosas/sage/local/lib/python2.6/site-packages/sage/misc/decorators.py", line 534, in wrapper
return func(*args, **options)
File "/cosas/sage/local/lib/python2.6/site-packages/sage/plot/contour_plot.py", line 470, in contour_plot
g, ranges = setup_for_eval_on_grid([f], [xrange, yrange], options['plot_points'])
File "/cosas/sage/local/lib/python2.6/site-packages/sage/plot/misc.py", line 144, in setup_for_eval_on_grid
return fast_float(funcs, *vars,**options), [tuple(range+[range_step]) for range,range_step in zip(ranges, range_steps)]
File "fast_eval.pyx", line 1357, in sage.ext.fast_eval.fast_float (sage/ext/fast_eval.c:8418)
File "fast_eval.pyx", line 1372, in sage.ext.fast_eval.fast_float (sage/ext/fast_eval.c:8627)
File "fast_callable.pyx", line 420, in sage.ext.fast_callable.fast_callable (sage/ext/fast_callable.c:3173)
File "expression.pyx", line 8108, in sage.symbolic.expression.Expression._fast_callable_ (sage/symbolic/expression.cpp:30640)
File "/cosas/sage/local/lib/python2.6/site-packages/sage/symbolic/expression_conversions.py", line 1392, in fast_callable
return FastCallableConverter(ex, etb)()
File "/cosas/sage/local/lib/python2.6/site-packages/sage/symbolic/expression_conversions.py", line 220, in __call__
return self.composition(ex, operator)
File "/cosas/sage/local/lib/python2.6/site-packages/sage/symbolic/expression_conversions.py", line 1370, in composition
return self.etb.call(function, *ex.operands())
File "fast_callable.pyx", line 685, in sage.ext.fast_callable.ExpressionTreeBuilder.call (sage/ext/fast_callable.c:5024)
File "fast_callable.pyx", line 565, in sage.ext.fast_callable.ExpressionTreeBuilder.__call__ (sage/ext/fast_callable.c:4378)
File "expression.pyx", line 8108, in sage.symbolic.expression.Expression._fast_callable_ (sage/symbolic/expression.cpp:30640)
File "/cosas/sage/local/lib/python2.6/site-packages/sage/symbolic/expression_conversions.py", line 1392, in fast_callable
return FastCallableConverter(ex, etb)()
File "/cosas/sage/local/lib/python2.6/site-packages/sage/symbolic/expression_conversions.py", line 220, in __call__
return self.composition(ex, operator)
File "/cosas/sage/local/lib/python2.6/site-packages/sage/symbolic/expression_conversions.py", line 1370, in composition
return self.etb.call(function, *ex.operands())
File "fast_callable.pyx", line 685, in sage.ext.fast_callable.ExpressionTreeBuilder.call (sage/ext/fast_callable.c:5024)
File "fast_callable.pyx", line 565, in sage.ext.fast_callable.ExpressionTreeBuilder.__call__ (sage/ext/fast_callable.c:4378)
File "expression.pyx", line 8108, in sage.symbolic.expression.Expression._fast_callable_ (sage/symbolic/expression.cpp:30640)
File "/cosas/sage/local/lib/python2.6/site-packages/sage/symbolic/expression_conversions.py", line 1392, in fast_callable
return FastCallableConverter(ex, etb)()
File "/cosas/sage/local/lib/python2.6/site-packages/sage/symbolic/expression_conversions.py", line 214, in __call__
return self.arithmetic(ex, operator)
File "/cosas/sage/local/lib/python2.6/site-packages/sage/symbolic/expression_conversions.py", line 1332, in arithmetic
return reduce(lambda x,y: self.etb.call(operator, x,y), operands)
File "/cosas/sage/local/lib/python2.6/site-packages/sage/symbolic/expression_conversions.py", line 1332, in <lambda>
return reduce(lambda x,y: self.etb.call(operator, x,y), operands)
File "fast_callable.pyx", line 685, in sage.ext.fast_callable.ExpressionTreeBuilder.call (sage/ext/fast_callable.c:5024)
File "fast_callable.pyx", line 565, in sage.ext.fast_callable.ExpressionTreeBuilder.__call__ (sage/ext/fast_callable.c:4378)
File "expression.pyx", line 8108, in sage.symbolic.expression.Expression._fast_callable_ (sage/symbolic/expression.cpp:30640)
File "/cosas/sage/local/lib/python2.6/site-packages/sage/symbolic/expression_conversions.py", line 1392, in fast_callable
return FastCallableConverter(ex, etb)()
File "/cosas/sage/local/lib/python2.6/site-packages/sage/symbolic/expression_conversions.py", line 213, in __call__
return self.arithmetic(div, div.operator())
File "/cosas/sage/local/lib/python2.6/site-packages/sage/symbolic/expression_conversions.py", line 1332, in arithmetic
return reduce(lambda x,y: self.etb.call(operator, x,y), operands)
File "/cosas/sage/local/lib/python2.6/site-packages/sage/symbolic/expression_conversions.py", line 1332, in <lambda>
return reduce(lambda x,y: self.etb.call(operator, x,y), operands)
File "fast_callable.pyx", line 685, in sage.ext.fast_callable.ExpressionTreeBuilder.call (sage/ext/fast_callable.c:5024)
File "fast_callable.pyx", line 565, in sage.ext.fast_callable.ExpressionTreeBuilder.__call__ (sage/ext/fast_callable.c:4378)
File "expression.pyx", line 8108, in sage.symbolic.expression.Expression._fast_callable_ (sage/symbolic/expression.cpp:30640)
File "/cosas/sage/local/lib/python2.6/site-packages/sage/symbolic/expression_conversions.py", line 1392, in fast_callable
return FastCallableConverter(ex, etb)()
File "/cosas/sage/local/lib/python2.6/site-packages/sage/symbolic/expression_conversions.py", line 204, in __call__
raise err
TypeError: cannot convert I to real number
I get a similar error when using `1j`, except it's
TypeError: Unable to convert 1.00000000000000*I to float; use abs() or
real_part() as desired
One work-around I've found is defining `f` as a regular python function:
z = var("z")
x,y = var("x,y",domain="real")
u = I*log(z)
def f(x,y): return imag_part(u(z=(x+I*y)))
contour_plot(f,(x,-3,3),(y,-3,3))
However it is much slower than ordinary plots.</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">ignamv</dc:creator><pubDate>Fri, 13 Apr 2012 09:48:28 +0200</pubDate><guid>https://ask.sagemath.org/question/7500/</guid></item><item><title>Contour Plots and Points</title><link>https://ask.sagemath.org/question/8584/contour-plots-and-points/</link><description>Why can I not have a single point on a contour plot?
var('x,y')
f(x,y)=sin(x)*cos(y)
G = contour_plot(f(x,y),(x,-3,3),(y,-3,3),contours=20,plot_points=100)
G += point((1,1), size=100)
G.show()
does not display the point. I can add a line (for example)
G += line(((1.5,1),(1.5,0)))
and that line shows up but not the point.
Thanks.
JT </description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">travis</dc:creator><pubDate>Sun, 15 Jan 2012 21:39:31 +0100</pubDate><guid>https://ask.sagemath.org/question/8584/</guid></item><item><title>contour_plot and figsize issue</title><link>https://ask.sagemath.org/question/8567/contour_plot-and-figsize-issue/</link><description>Hello!
I am trying to make contour_plot of function and then get result image with custom size using **show** and keywork **figsize**.
The strange thing: this code actually ignores **figsize** keyword:
x,y = var('x,y')
contour_plot(cos(x^2+y^2), (x, -4, 4), (y, -4, 4)).show(xmin=-4,xmax=4,ymin=-4,ymax=4,figsize=(10,6))
But this one respects:
(point((0,0))+contour_plot(cos(x^2+y^2), (x, -4, 4), (y, -4, 4))).show(xmin=-4,xmax=4,ymin=-4,ymax=4,figsize=(8,2))
How to set figsize for contour_plot properly?</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Eugene</dc:creator><pubDate>Fri, 16 Dec 2011 08:26:56 +0100</pubDate><guid>https://ask.sagemath.org/question/8567/</guid></item><item><title>Contour Plot not working with pseudo-piecewise function</title><link>https://ask.sagemath.org/question/8370/contour-plot-not-working-with-pseudo-piecewise-function/</link><description>Hi,
I'm fairly new to Sage and don't know if this is a bug or just my own limited understanding. I want to plot a function 'f(g1, g2)' but only in some relevant area of the plot. All other points should display/evaluate to zero. This should work fine in Octave or numpy but Sage for some reason gives me an error-message which I fail to understand.
Function assignment like so:
def f(g1, g2):
if g1*g2 > 0.0:
if abs(g2) < 1/abs(g1):
return sqrt(0.5*((1+g1*g2)*abs(g1+g2))/(sqrt((1.0-g1*g2)^3)*g1*g2))
else:
return 0
Then the Plot:
var('g1 g2')
contour_plot(f(g1,g2), (g1,-4,4), (g2,-4,4),plot_points=500, cmap='afmhot_r', colorbar=True, contours=srange(1,6,0.5))
and at last the error-message:
ValueError: zero-size array to ufunc.reduce without identity
Strangely, if I assign a single number to 'contours' (or leave it out to get the default value) the error-message does not show but instead I get an empty/white plot.
If I do not use a conditional/if-statement in my function-assignment the contour-plot shows just fine (except that it didn't do what I wanted).
Does anyone know how to fix this or why it doesn't work or at least why I'm being silly for even trying it that way?
Thanks in advance
</description><dc:creator xmlns:dc="http://purl.org/dc/elements/1.1/">Jonathan.B</dc:creator><pubDate>Sun, 09 Oct 2011 19:05:01 +0200</pubDate><guid>https://ask.sagemath.org/question/8370/</guid></item></channel></rss>