Revision history [back]
 | 1 | initial version |
I have not tested it on 10-vertex, 11-edge graphs, and its correctness has not been verified on a large number of examples.
good_graphs = []
for g in graphs.nauty_geng("5 6 -c"): # 5-vertex 6 edges if spectra_diff_one_edge(g): good_graphs.append(g)
def spectra_diff_one_edge(g, return_info=False):
"""
Check if there exists an edge that can be added to graph g such that
the Laplacian spectrum changes in exactly one eigenvalue.
Parameters:
g (Graph): a Sage graph
return_info (bool):
- If True, return (u, v, old_val, new_val) for the edge that
changes exactly one eigenvalue.
- If False, return True/False indicating whether such an edge exists.
Returns:
If return_info=False:
bool: True if such an edge exists, otherwise False
If return_info=True:
tuple or None: (u, v, old_val, new_val) if an edge exists that changes
exactly one eigenvalue, otherwise None
"""
base_spec = sorted([RR(x) for x in g.laplacian_matrix().eigenvalues()])
comp = g.complement()
for (u, v) in comp.edges(labels=False):
g.add_edge(u, v)
new_spec = sorted([RR(x) for x in g.laplacian_matrix().eigenvalues()])
g.delete_edge(u, v)
# Find the eigenvalue differences
diffs = [(a, b) for a, b in zip(base_spec, new_spec) if abs(a-b) > 1e-6]
if len(diffs) == 1:
old_val, new_val = diffs[0]
if return_info:
return f"Adding edge ({u},{v}) changes the eigenvalue from {old_val} to {new_val}"
else:
return True
# No edge found that satisfies the condition
return False if not return_info else None
 | 2 | No.2 Revision |
I have not tested it on 10-vertex, 11-edge graphs, and its correctness has not been verified on a large number of examples.
 | 3 | No.3 Revision |
I have not tested it on 10-vertex, 11-edge graphs, and its correctness has not been verified on a large number of examples.
good_graphs = []
for g in graphs.nauty_geng("5 6 -c"): # 5-vertex 6 edges
if spectra_diff_one_edge(g):
good_graphs.append(g)
### function
def spectra_diff_one_edge(g, return_info=False):
"""
Check if there exists an edge that can be added to graph g such that
the Laplacian spectrum changes in exactly one eigenvalue.
Parameters:
g (Graph): a Sage graph
return_info (bool):
- If True, return (u, v, old_val, new_val) for the edge that
changes exactly one eigenvalue.
- If False, return True/False indicating whether such an edge exists.
Returns:
If return_info=False:
bool: True if such an edge exists, otherwise False
If return_info=True:
tuple or None: (u, v, old_val, new_val) if an edge exists that changes
exactly one eigenvalue, otherwise None
"""
base_spec = sorted([RR(x) for x in g.laplacian_matrix().eigenvalues()])
comp = g.complement()
for (u, v) in comp.edges(labels=False):
g.add_edge(u, v)
new_spec = sorted([RR(x) for x in g.laplacian_matrix().eigenvalues()])
g.delete_edge(u, v)
# Find the eigenvalue differences
diffs = [(a, b) for a, b in zip(base_spec, new_spec) if abs(a-b) > 1e-6]
if len(diffs) == 1:
old_val, new_val = diffs[0]
if return_info:
return f"Adding edge ({u},{v}) changes the eigenvalue from {old_val} to {new_val}"
else:
return True
# No edge found that satisfies the condition
return False if not return_info else None
 | 4 | No.4 Revision |
I have not tested it on 10-vertex, 11-edge graphs, and its correctness has not been verified on a large number of examples.
good_graphs = []
for g in graphs.nauty_geng("5 6 -c"): # 5-vertex 6 edges
if spectra_diff_one_edge(g):
good_graphs.append(g)
### function
from collections import Counter
def one_value_change(list1, list2, tol=1e-6):
"""
Check if two lists differ by exactly one value (considering multiplicity and tolerance).
Parameters:
list1, list2 : lists of numbers
tol : float, two numbers within tol are considered equal
Returns:
(bool, old_value, new_value) :
- True and the changed values if exactly one element differs
- False, None, None otherwise
"""
def multiset(seq):
# Round each number to tol precision
return Counter(round(x / tol) * tol for x in seq)
c1 = multiset(list1)
c2 = multiset(list2)
diff1 = c1 - c2
diff2 = c2 - c1
if len(diff1) == 1 and len(diff2) == 1:
old_val = list(diff1.elements())[0]
new_val = list(diff2.elements())[0]
return True, old_val, new_val
else:
return False, None, None
def spectra_diff_one_edge(g, return_info=False):
return_info=False, tol=1e-6):
"""
Check if there exists an edge that can be added to graph g such that
the Laplacian spectrum changes in exactly one eigenvalue.
Parameters:
g (Graph): a Sage graph
return_info (bool):
- If True, return (u, v, old_val, new_val) for the edge that
changes exactly one eigenvalue.
- If False, return True/False indicating whether such an edge exists.
tol (float): tolerance for eigenvalue comparison
Returns:
If return_info=False:
bool: True if such an edge exists, otherwise False
If return_info=True:
tuple or None: (u, v, old_val, new_val) if an edge exists that changes
exactly one eigenvalue, otherwise None
"""
base_spec = sorted([RR(x) [RR(x) for x in g.laplacian_matrix().eigenvalues()])
g.laplacian_matrix().eigenvalues()]
comp = g.complement()
for (u, v) in comp.edges(labels=False):
g.add_edge(u, v)
new_spec = sorted([RR(x) [RR(x) for x in g.laplacian_matrix().eigenvalues()])
g.laplacian_matrix().eigenvalues()]
g.delete_edge(u, v)
# Find the eigenvalue differences
diffs = [(a, b) for a, b in zip(base_spec, new_spec) if abs(a-b) > 1e-6]
if len(diffs) == 1:
changed, old_val, new_val = diffs[0]
one_value_change(base_spec, new_spec, tol)
if changed:
if return_info:
return f"Adding edge ({u},{v}) changes the eigenvalue from {old_val} to {new_val}"
(u, v, old_val, new_val)
else:
return True
# No edge found that satisfies the condition
return False if not return_info else None
 | 5 | No.5 Revision |
I have not tested it on 10-vertex, 11-edge graphs, and its correctness has not been verified on a large number of examples.
good_graphs = []
for g in graphs.nauty_geng("5 6 -c"): # 5-vertex 6 edges
if spectra_diff_one_edge(g):
good_graphs.append(g)
### function
from collections import Counter
Counter
def one_value_change(list1, list2, tol=1e-6):
"""
Check if two lists differ by exactly one value (considering multiplicity and tolerance).
Parameters:
list1, list2 : lists of numbers
tol : float, two numbers within tol are considered equal
Returns:
(bool, old_value, new_value) :
- True and the changed values if exactly one element differs
- False, None, None otherwise
"""
def multiset(seq):
# Round each number to tol precision
return Counter(round(x / tol) * tol for x in seq)
c1 = multiset(list1)
c2 = multiset(list2)
diff1 = c1 - c2
diff2 = c2 - c1
if len(diff1) == 1 and len(diff2) == 1:
old_val = list(diff1.elements())[0]
new_val = list(diff2.elements())[0]
return True, old_val, new_val
else:
return False, None, None
def spectra_diff_one_edge(g, return_info=False, tol=1e-6):
"""
Check if there exists an edge that can be added to graph g such that
the Laplacian spectrum changes in exactly one eigenvalue.
Parameters:
g (Graph): a Sage graph
return_info (bool):
- If True, return (u, v, old_val, new_val) for the edge that
changes exactly one eigenvalue.
- If False, return True/False indicating whether such an edge exists.
tol (float): tolerance for eigenvalue comparison
Returns:
If return_info=False:
bool: True if such an edge exists, otherwise False
If return_info=True:
tuple or None: (u, v, old_val, new_val) if an edge exists that changes
exactly one eigenvalue, otherwise None
"""
base_spec = [RR(x) for x in g.laplacian_matrix().eigenvalues()]
comp = g.complement()
for (u, v) in comp.edges(labels=False):
g.add_edge(u, v)
new_spec = [RR(x) for x in g.laplacian_matrix().eigenvalues()]
g.delete_edge(u, v)
changed, old_val, new_val = one_value_change(base_spec, new_spec, tol)
if changed:
if return_info:
return (u, v, old_val, new_val)
else:
return True
return False if not return_info else None
 | 6 | No.6 Revision |
I have not tested it on 10-vertex, 11-edge graphs, and its correctness has not been verified on a large number of examples.
good_graphs = []
for g in graphs.nauty_geng("5 6 -c"): # 5-vertex 6 edges
if spectra_diff_one_edge(g):
good_graphs.append(g)
### function
key function
from collections import Counter
def one_value_change(list1, list2, tol=1e-6):
"""
Check if two lists differ by exactly one value (considering multiplicity and tolerance).
Parameters:
list1, list2 : lists of numbers
tol : float, two numbers within tol are considered equal
Returns:
(bool, old_value, new_value) :
- True and the changed values if exactly one element differs
- False, None, None otherwise
"""
def multiset(seq):
# Round each number to tol precision
return Counter(round(x / tol) * tol for x in seq)
c1 = multiset(list1)
c2 = multiset(list2)
diff1 = c1 - c2
diff2 = c2 - c1
if len(diff1) == 1 and len(diff2) == 1:
old_val = list(diff1.elements())[0]
new_val = list(diff2.elements())[0]
return True, old_val, new_val
else:
return False, None, None
def spectra_diff_one_edge(g, return_info=False, tol=1e-6):
"""
Check if there exists an edge that can be added to graph g such that
the Laplacian spectrum changes in exactly one eigenvalue.
Parameters:
g (Graph): a Sage graph
return_info (bool):
- If True, return (u, v, old_val, new_val) for the edge that
changes exactly one eigenvalue.
- If False, return True/False indicating whether such an edge exists.
tol (float): tolerance for eigenvalue comparison
Returns:
If return_info=False:
bool: True if such an edge exists, otherwise False
If return_info=True:
tuple or None: (u, v, old_val, new_val) if an edge exists that changes
exactly one eigenvalue, otherwise None
"""
base_spec = [RR(x) for x in g.laplacian_matrix().eigenvalues()]
comp = g.complement()
for (u, v) in comp.edges(labels=False):
g.add_edge(u, v)
new_spec = [RR(x) for x in g.laplacian_matrix().eigenvalues()]
g.delete_edge(u, v)
changed, old_val, new_val = one_value_change(base_spec, new_spec, tol)
if changed:
if return_info:
return (u, v, old_val, new_val)
else:
return True
return False if not return_info else None
 | 7 | No.7 Revision |
I have not tested it on 10-vertex, 11-edge graphs, and its correctness has not been verified on a large number of examples.
good_graphs = []
for g in graphs.nauty_geng("5 6 -c"): # 5-vertex 6 edges
if spectra_diff_one_edge(g):
good_graphs.append(g)
key function
from collections import Counter
def one_value_change(list1, list2, tol=1e-6):
"""
Check if two lists differ by exactly one value (considering multiplicity and tolerance).
Parameters:
list1, list2 : lists of numbers
tol : float, two numbers within tol are considered equal
Returns:
(bool, old_value, new_value) :
- True and the changed values if exactly one element differs
- False, None, None otherwise
"""
def multiset(seq):
# Round each number to tol precision
return Counter(round(x / tol) * tol for x in seq)
c1 = multiset(list1)
c2 = multiset(list2)
diff1 = c1 - c2
diff2 = c2 - c1
if len(diff1) == 1 and len(diff2) == 1:
old_val = list(diff1.elements())[0]
new_val = list(diff2.elements())[0]
return True, old_val, new_val
else:
return False, None, None
def spectra_diff_one_edge(g, return_info=False, tol=1e-6):
"""
Check if there exists an edge that can be added to graph g such that
the Laplacian spectrum changes in exactly one eigenvalue.
Parameters:
g (Graph): a Sage graph
return_info (bool):
- If True, return (u, v, old_val, new_val) for the edge that
changes exactly one eigenvalue.
- If False, return True/False indicating whether such an edge exists.
tol (float): tolerance for eigenvalue comparison
Returns:
If return_info=False:
bool: True if such an edge exists, otherwise False
If return_info=True:
tuple or None: (u, v, old_val, new_val) if an edge exists that changes
exactly one eigenvalue, otherwise None
"""
base_spec = [RR(x) for x in g.laplacian_matrix().eigenvalues()]
comp = g.complement()
for (u, v) in comp.edges(labels=False):
g.add_edge(u, v)
new_spec = [RR(x) for x in g.laplacian_matrix().eigenvalues()]
g.delete_edge(u, v)
changed, old_val, new_val = one_value_change(base_spec, new_spec, tol)
if changed:
if return_info:
return (u, v, old_val, new_val)
else:
return True
return False if not return_info else None
 | 8 | No.8 Revision |
I have not tested it on 10-vertex, 11-edge graphs, and its correctness has not been verified on a large number of examples.
good_graphs = []
for g in graphs.nauty_geng("5 6 -c"): # 5-vertex 6 edges
if spectra_diff_one_edge(g):
good_graphs.append(g)
key function
from collections import Counter
def one_value_change(list1, list2, tol=1e-6):
"""
Check if two lists differ by exactly one value (considering multiplicity and tolerance).
Parameters:
list1, list2 : lists of numbers
tol : float, two numbers within tol are considered equal
Returns:
(bool, old_value, new_value) :
- True and the changed values if exactly one element differs
- False, None, None otherwise
"""
def multiset(seq):
# Round each number to tol precision
return Counter(round(x / tol) * tol for x in seq)
c1 = multiset(list1)
c2 = multiset(list2)
diff1 = c1 - c2
diff2 = c2 - c1
if len(diff1) == 1 and len(diff2) == 1:
old_val = list(diff1.elements())[0]
new_val = list(diff2.elements())[0]
return True, old_val, new_val
else:
return False, None, None
def spectra_diff_one_edge(g, return_info=False, tol=1e-6):
"""
Check if there exists an edge that can be added to graph g such that
the Laplacian spectrum changes in exactly one eigenvalue.
Parameters:
g (Graph): a Sage graph
return_info (bool):
- If True, return (u, v, old_val, new_val) for the edge that
changes exactly one eigenvalue.
- If False, return True/False indicating whether such an edge exists.
tol (float): tolerance for eigenvalue comparison
Returns:
If return_info=False:
bool: True if such an edge exists, otherwise False
If return_info=True:
tuple or None: (u, v, old_val, new_val) if an edge exists that changes
exactly one eigenvalue, otherwise None
"""
base_spec = [RR(x) for x in g.laplacian_matrix().eigenvalues()]
comp = g.complement()
for (u, v) in comp.edges(labels=False):
g.add_edge(u, v)
new_spec = [RR(x) for x in g.laplacian_matrix().eigenvalues()]
g.delete_edge(u, v)
changed, old_val, new_val = one_value_change(base_spec, new_spec, tol)
if changed:
if return_info:
return (u, v, old_val, new_val)
else:
return True
return False if not return_info else None
For exmaple, I will get two graphs by running the above codes.
g=good_graphs[0]
g.show()
g.laplacian_matrix().eigenvalues()
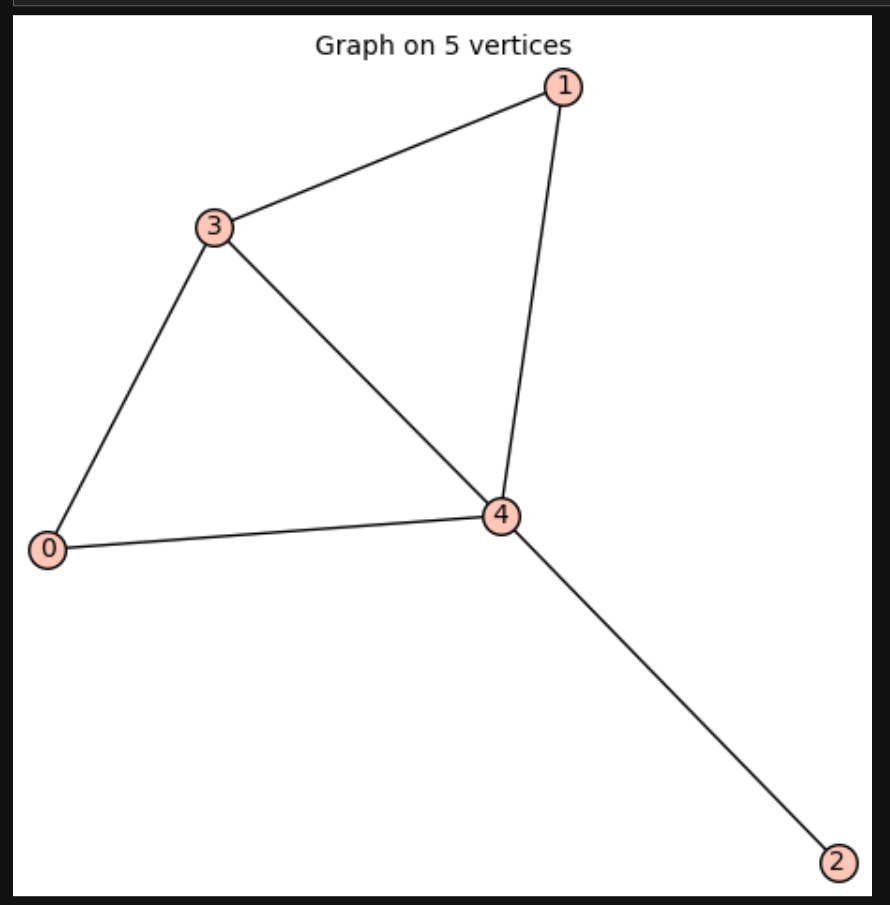
[5, 4, 2, 1, 0]
spectra_diff_one_edge(g, return_info=True, tol=1e-6)
It gives (0, 1, 2.00000000000000, 4.00000000000000)
which means that add the edge (0,1) will change only one eigenvalue.
g.add_edge(0, 1)
print(g.laplacian_matrix().eigenvalues())
[5, 1, 0, 4, 4]
We compare the symmetric difference of the two lists, and only the values 2 and 4 are different, while all the others match. (Here, note that I’m a bit unsure about your exact meaning of a position change—my understanding is that only two values are different.)
