Revision history [back]

It turns out that the brute-force exploration is, in this case, not too long. Run :

def principal_submatrix(m, s, sort=False):
    if sort:
        s = sorted(s)
    return m[s, s]

# Generator of graphs conforming to requirements

def gen_bicycles():
    for g in graphs.nauty_geng("10 -c"):
        if g.size()==11:
            A=g.adjacency_matrix()
            if all(map(lambda s:bool(principal_submatrix(A, s, sort=True).rank()==8),
                       Subsets(range(10), 9))):
                yield g

Then, the list of such graphs can be generated by :

sage: L=[]
sage: GB=gen_bicycles()
sage: %time for g in GB: L+=[g]
CPU times: user 1min 46s, sys: 32 ms, total: 1min 46s
Wall time: 1min 46s
sage: len(L)
171

HTH,

It turns out that the brute-force exploration is, in this case, not too long. Run :

def principal_submatrix(m, s, sort=False):
    if sort:
        s = sorted(s)
    return m[s, s]

# Generator of graphs conforming to requirements

def gen_bicycles():
    for g in graphs.nauty_geng("10 -c"):
        if g.size()==11:
            A=g.adjacency_matrix()
            if all(map(lambda s:bool(principal_submatrix(A, s, sort=True).rank()==8),
                       Subsets(range(10), Subsets(g.vertices(), 9))):
                yield g

Then, the list of such graphs can be generated by :

sage: L=[]
sage: GB=gen_bicycles()
sage: %time for g in GB: L+=[g]
CPU times: user 1min 46s, sys: 32 ms, total: 1min 46s
Wall time: 1min 46s
sage: len(L)
171
sage: L[choice(range(len(L)))].plot()
Launched png viewer for Graphics object consisting of 22 graphics primitives

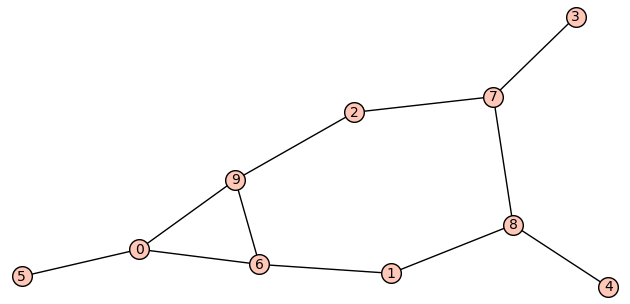
HTH,