Revision history [back]

Let us start from showing the images of lines y=kx using the section of the graph with the Oxz plane

var('x y z theta rho')
T = Cylindrical('height', ['radius', 'azimuth'])
T.transform(radius=rho, azimuth=theta, height=z)
p=plot3d(cos(theta)*exp(-rho^2),(rho, 0, 2), (theta, 0, pi), transformation=T,
         mesh=true,plot_points=[15,30],thickness=0.6,opacity=0,aspect_ratio=[1,1,1.8])
p1=parametric_plot3d([0,0,z],(z,-1.2,1.2),color='blue',thickness=2,frame=False)
p2=parametric_plot3d([x,0,0],(x,-2.3,2.3),color='blue',thickness=2,frame=False)
po2 = {'fontsize': 20, 'color': 'black'}
t1 = text3d("z", (0,0,1.3),**po2)
t2 = text3d("x", (2.4,0,0),**po2)
(p+p1+p2+t1+t2).rotateZ(-pi/1.55)

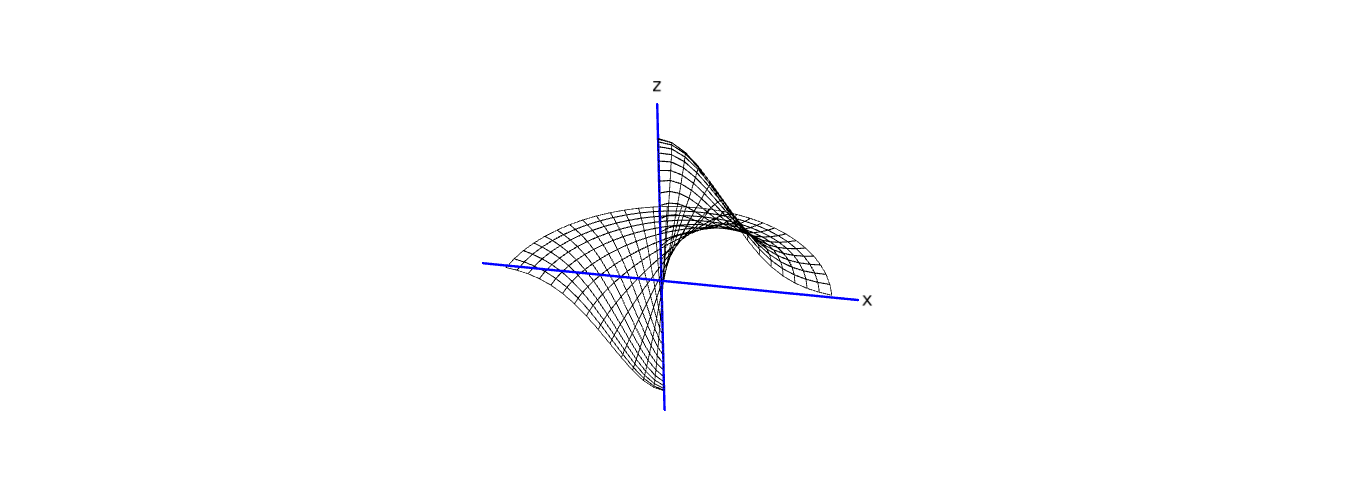
The 3d-graphics, the symmetry property: f(-x,y)=-f(x,y) and the calculations:

var("x, y, rho, theta, k");
f(x,y)=x*exp(-x^2-y^2)/sqrt(x^2+y^2)
h(x)=f(x, y).subs({y:k*x})
l=h(x).limit(x=0, dir='-')
r=h(x).limit(x=0, dir='+')
(r,l)

(1/sqrt(k^2 + 1), -1/sqrt(k^2 + 1))

h(x).limit(x=0)

und

show that sage is right - the two-sided directional limits are undefined (for finite k)

Let us check the one-sided limits with k=tan(theta)

f(x, y).subs({y:x*tan(theta)}).limit(x=0,dir='+')

1/sqrt(tan(theta)^2 + 1)

If -pi/2 < theta < pi/2, r>0; we have

1/(tan(theta)^2+1) = cos(theta)^2 and cos(theta)>0,

so for k=tan(theta): 1/sqrt(k^2+1)=cos(theta)

For pi/2 < theta < 3pi/2 where cos(theta)<0 we have

f(x, y).subs({y:x*tan(theta)}).limit(x=0,dir='-')

-1/sqrt(tan(theta)^2 + 1)

so as before

-1/sqrt(k^2+1)=-sqrt(cos(theta)^2)=-(-cos(theta))=cos(theta)

For theta=pi/2 or 3pi/2 we have x=0 so f(x,y)=0 and the corresponding limit is 0=cos(theta).

In this case the limit is two-sided.