Revision history [back]

Well... the problem seems to arise from the label=False option. Without it :

sage: [u.edges() for u in g.acyclic_orientations()]
[[(1, 0, 0), (1, 2, 0), (2, 0, 1), (3, 0, 0), (3, 2, 0)],
 [(1, 0, 0), (1, 2, 0), (2, 0, 1), (3, 0, 1), (3, 2, 0)],
 [(1, 0, 1), (1, 2, 0), (2, 0, 1), (3, 0, 0), (3, 2, 0)],
 [(1, 0, 0), (1, 2, 0), (2, 0, 1), (3, 0, 1), (3, 2, 1)],
 [(1, 0, 1), (1, 2, 1), (2, 0, 1), (3, 0, 0), (3, 2, 0)],
 [(1, 0, 1), (1, 2, 0), (2, 0, 1), (3, 0, 1), (3, 2, 0)],
 [(1, 0, 1), (1, 2, 0), (2, 0, 1), (3, 0, 1), (3, 2, 1)],
 [(1, 0, 1), (1, 2, 1), (2, 0, 1), (3, 0, 1), (3, 2, 0)],
 [(1, 0, 1), (1, 2, 1), (2, 0, 1), (3, 0, 1), (3, 2, 1)],
 [(1, 0, 0), (1, 2, 0), (2, 0, 0), (3, 0, 0), (3, 2, 0)],
 [(1, 0, 0), (1, 2, 0), (2, 0, 0), (3, 0, 0), (3, 2, 1)],
 [(1, 0, 0), (1, 2, 1), (2, 0, 0), (3, 0, 0), (3, 2, 0)],
 [(1, 0, 0), (1, 2, 1), (2, 0, 0), (3, 0, 0), (3, 2, 1)],
 [(1, 0, 0), (1, 2, 0), (2, 0, 0), (3, 0, 1), (3, 2, 1)],
 [(1, 0, 1), (1, 2, 1), (2, 0, 0), (3, 0, 0), (3, 2, 0)],
 [(1, 0, 0), (1, 2, 1), (2, 0, 0), (3, 0, 1), (3, 2, 1)],
 [(1, 0, 1), (1, 2, 1), (2, 0, 0), (3, 0, 0), (3, 2, 1)],
 [(1, 0, 1), (1, 2, 1), (2, 0, 0), (3, 0, 1), (3, 2, 1)]]

The label carries the orientation of an edge. Quick check of the unicity :

sage: len([u.edges() for u in g.acyclic_orientations()])
18
sage: Set(([u.edges() for u in g.acyclic_orientations()])).cardinality()
18

The problem is therefore that print( an edge , label=False) merely suppresses the label. In this special case, it might be pertinent to reverse the order of the edges if the label is 1 ; however, the pertinence of this change in the more general cases of graph printing is to be checked...

HTH,

Well... the problem seems to arise from the label=False option. Without it :

sage: [u.edges() for u in g.acyclic_orientations()]
[[(1, 0, 0), (1, 2, 0), (2, 0, 1), (3, 0, 0), (3, 2, 0)],
 [(1, 0, 0), (1, 2, 0), (2, 0, 1), (3, 0, 1), (3, 2, 0)],
 [(1, 0, 1), (1, 2, 0), (2, 0, 1), (3, 0, 0), (3, 2, 0)],
 [(1, 0, 0), (1, 2, 0), (2, 0, 1), (3, 0, 1), (3, 2, 1)],
 [(1, 0, 1), (1, 2, 1), (2, 0, 1), (3, 0, 0), (3, 2, 0)],
 [(1, 0, 1), (1, 2, 0), (2, 0, 1), (3, 0, 1), (3, 2, 0)],
 [(1, 0, 1), (1, 2, 0), (2, 0, 1), (3, 0, 1), (3, 2, 1)],
 [(1, 0, 1), (1, 2, 1), (2, 0, 1), (3, 0, 1), (3, 2, 0)],
 [(1, 0, 1), (1, 2, 1), (2, 0, 1), (3, 0, 1), (3, 2, 1)],
 [(1, 0, 0), (1, 2, 0), (2, 0, 0), (3, 0, 0), (3, 2, 0)],
 [(1, 0, 0), (1, 2, 0), (2, 0, 0), (3, 0, 0), (3, 2, 1)],
 [(1, 0, 0), (1, 2, 1), (2, 0, 0), (3, 0, 0), (3, 2, 0)],
 [(1, 0, 0), (1, 2, 1), (2, 0, 0), (3, 0, 0), (3, 2, 1)],
 [(1, 0, 0), (1, 2, 0), (2, 0, 0), (3, 0, 1), (3, 2, 1)],
 [(1, 0, 1), (1, 2, 1), (2, 0, 0), (3, 0, 0), (3, 2, 0)],
 [(1, 0, 0), (1, 2, 1), (2, 0, 0), (3, 0, 1), (3, 2, 1)],
 [(1, 0, 1), (1, 2, 1), (2, 0, 0), (3, 0, 0), (3, 2, 1)],
 [(1, 0, 1), (1, 2, 1), (2, 0, 0), (3, 0, 1), (3, 2, 1)]]

The label carries the orientation of an edge. Quick check of the unicity :

sage: len([u.edges() for u in g.acyclic_orientations()])
18
sage: Set(([u.edges() for u in g.acyclic_orientations()])).cardinality()
18

EDIT : The problem may be more extensive that it seems :

sage: graphics_array([plot(u) for u in g.acyclic_orientations()], nrows=6, ncols
....: =3)
Launched png viewer for Graphics Array of size 6 x 3

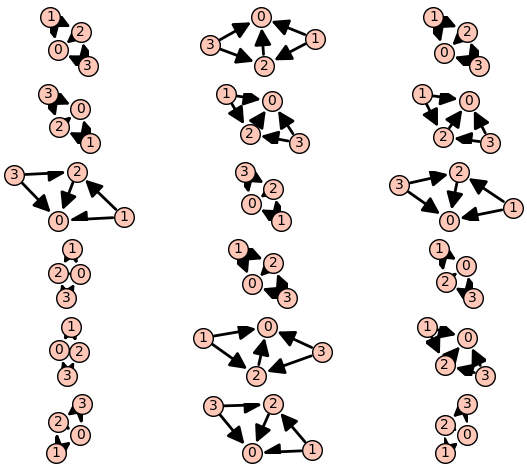
image description

which is eighteen copies of the same directed graph.

Workaround :

sage: def fix(e):return tuple([e[1], e[0]]) if e[2] else tuple([e[0], e[1]])
sage: graphics_array([plot(DiGraph([fix(u) for u in v.edges()])) for v in g.acyc
....: lic_orientations()], nrows=6, ncols=3)
Launched png viewer for Graphics Array of size 6 x 3

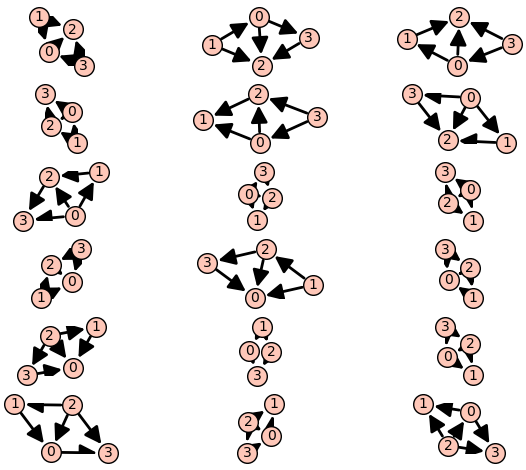
image description

which seems correct.

This is probably worth of a Github ticket (by someone more versed in graph theory and its Sage implementation(s) than I am...).

HTH,