Revision history [back]

I would suggest that you try implementing the feature yourself. There are basically three options available to express your tiling problem.

Which one to use depend on the tiling problem you want to solve (you might want to try all of them and convert your tiling problem with various encoding and use various solvers).

For example, here is an implementation of domino tiling of a rectangle with horizontal and vertical resources constraints using a mixed integer linear program

def rectangle_domino_tiling(width, height, num_horiz, num_vert):
    from sage.numerical.mip import MIPSolverException

    M = MixedIntegerLinearProgram()

    # h[i,j]: whether there is a horizontal domino at position i,j
    # v[i,j]: whether there is a vertical domino at position i,j
    h = M.new_variable(binary=True)
    v = M.new_variable(binary=True)

    # tiling constraints
    for i in range(width):
        for j in range(height):
            s = 0
            if i > 0:
                s += h[i-1, j]
            if j > 0:
                s += v[i, j-1]
            if i < width - 1:
                s += h[i, j]
            if j < height - 1:
                s += v[i,j]
            M.add_constraint(s == 1)

    # resource constraints
    M.add_constraint(M.sum(h[i,j] for i in range(width - 1) for j in range(height)) == num_horiz)
    M.add_constraint(M.sum(v[i,j] for i in range(width) for j in range(height - 1)) == num_vert)

    try:
        M.solve()
    except MIPSolverException:
        # no solution
        return None

    hval = M.get_values(h)
    vval = M.get_values(v)

    return ([(i, j) for i in range(width - 1) for j in range(height) if hval[i, j]],
            [(i, j) for i in range(width) for j in range(height - 1) if vval[i, j]])

def plot_tiling(width, height, horizontal_dominos, vertical_dominos):
    G = Graphics()
    for i, j in horizontal_dominos:
        G += polygon2d([(i, j), (i + 2, j), (i + 2, j + 1), (i, j + 1)], color='blue', edgecolor='black', alpha=0.5)
    for i, j in vertical_dominos:
        G += polygon2d([(i, j), (i + 1, j), (i + 1, j + 2), (i, j + 2)], color='red', edgecolor='black', alpha=0.5)
    G.axes(False)
    G.set_aspect_ratio(1)
    return G

Here is an example of how to use these functions

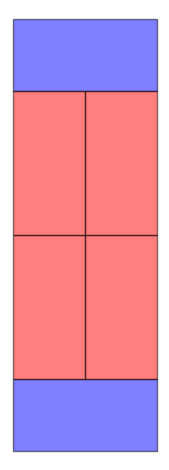
sage: hsol, vsol = rectangle_domino_tiling(4, 4, 2, 6)
sage: plot_tiling(4, 4, hsol, vsol)

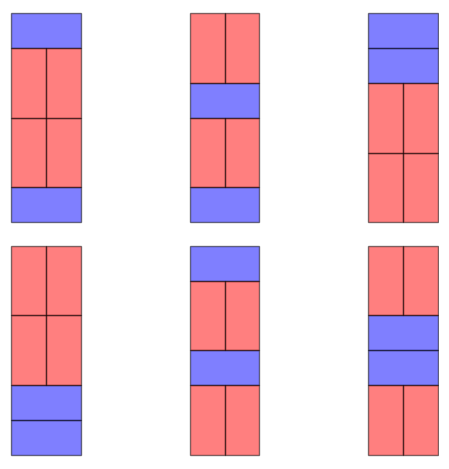
image description

sage: hsol, vsol = rectangle_domino_tiling(2, 6, 2, 4)
sage: plot_tiling(2, 6, hsol, vsol)

image description

I would suggest that you try implementing the feature yourself. There are basically three options available to express your tiling problem.

Which one to use depend on the tiling problem you want to solve (you might want to try all of them and convert your tiling problem with various encoding and use various solvers).

For example, here is an implementation of domino tiling of a rectangle with horizontal and vertical resources constraints using a mixed integer linear program

def rectangle_domino_tiling(width, rectangle_domino_tilings(width, height, num_horiz, num_vert):
    from sage.numerical.mip import MIPSolverException

    M = MixedIntegerLinearProgram()

    # h[i,j]: whether there is a horizontal domino at position i,j
    # v[i,j]: whether there is a vertical domino at position i,j
    h = M.new_variable(binary=True)
    v = M.new_variable(binary=True)

    num_pieces = (width * height) // 2

    # tiling constraints
    for i in range(width):
        for j in range(height):
            s = 0
            if i > 0:
                s += h[i-1, j]
            if j > 0:
                s += v[i, j-1]
            if i < width - 1:
                s += h[i, j]
            if j < height - 1:
                s += v[i,j]
v[i, j]
            M.add_constraint(s == 1)

    # resource constraints
    M.add_constraint(M.sum(h[i,j] M.add_constraint(M.sum(h[i, j] for i in range(width - 1) for j in range(height)) == num_horiz)
    M.add_constraint(M.sum(v[i,j] M.add_constraint(M.sum(v[i, j] for i in range(width) for j in range(height - 1)) == num_vert)

    while True:
        try:
         M.solve()
     except MIPSolverException:
         # no solution
        return None

    break

        hval = M.get_values(h)
     vval = M.get_values(v)

    return     # yield the solution
        yield ([(i, j) for i in range(width - 1) for j in range(height) if hval[i, j]],
             [(i, j) for i in range(width) for j in range(height - 1) if vval[i, j]])

        # exclude the solution for next iteration
        M.add_constraint(M.sum(h[i, j] for i in range(width - 1) for j in range(height) if hval[i,j])
                         + M.sum(v[i, j] for i in range(width) for j in range(height - 1) if vval[i, j])
                         <= num_pieces - 1)


def plot_tiling(width, height, horizontal_dominos, vertical_dominos):
    G = Graphics()
    for i, j in horizontal_dominos:
        G += polygon2d([(i, j), (i + 2, j), (i + 2, j + 1), (i, j + 1)], color='blue', edgecolor='black', alpha=0.5)
    for i, j in vertical_dominos:
        G += polygon2d([(i, j), (i + 1, j), (i + 1, j + 2), (i, j + 2)], color='red', edgecolor='black', alpha=0.5)
    G.axes(False)
    G.set_aspect_ratio(1)
    return G

Here is an example of how to use these functions

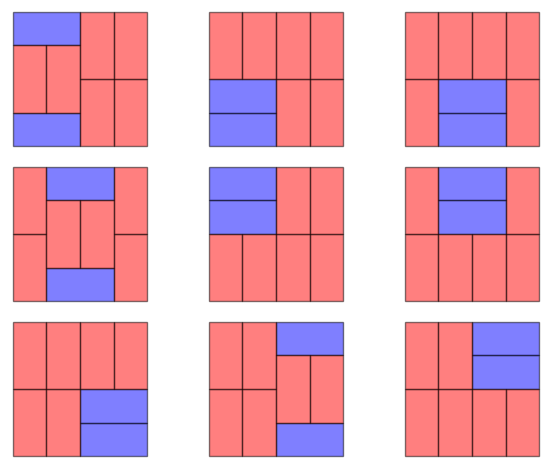
sage: solutions = list(rectangle_domino_tilings(4, 4, 2, 6))
sage: len(solutions)
sage: graphics_array([plot_tiling(4, 4, hsol, vsol) for hsol, vsol = rectangle_domino_tiling(4, 4, 2, 6)
sage: plot_tiling(4, 4, hsol, vsol)
in solutions], 3, 3)

image description

sage: solutions = list(rectangle_domino_tilings(2, 6, 2, 4))
sage: len(solutions)
6
sage:  graphics_array([plot_tiling(2, 6, hsol, vsol) for hsol, vsol = rectangle_domino_tiling(2, 6, in solutions], 2, 4)
sage: plot_tiling(2, 6, hsol, vsol)
3)

image description