Revision history [back]
 | 1 | initial version |
I finally got to a result using a completely different approach. First I noticed $\rho$ and $\beta$ are one and the same variable as numerical approximative values suggest. That brings down the number of varialbles from 11 to 10. My sincere appologies for not picking that up earlier. Then, rewriting the set of equations as a linear system of the complex field yields
$$ l \left(\begin{array}{rrrrr} 1 & 0 & 0 & 0 & 0 \ -1 & -1 & 0 & 0 & 0 \ -1 & 1 & 0 & 1 & 0 \ -1 & 0 & 0 & 1 & -1 \ 0 & 0 & 1 & 0 & 1 \end{array}\right) \left(\begin{array}{r} e^{\left(i \, \beta\right)} \ e^{\left(i \, \gamma\right)} \ e^{\left(i \, c\right)} \ e^{\left(i \, d\right)} \ e^{\left(i \, e\right)}
\end{array}\right)
\left(\begin{array}{r} -l {\left(-i \, \sqrt{3} + 4\right)} e^{\left(i \, \alpha\right)} + 1 \ \frac{1}{2} \, l {\left(-i \, \sqrt{3} - 3\right)} e^{\left(i \, \alpha\right)} + l e^{\left(i \, \delta\right)} + i \ \frac{1}{2} \, l {\left(-i \, \sqrt{3} + 3\right)} e^{\left(i \, \alpha\right)} - l e^{\left(i \, a\right)} - l e^{\left(i \, \delta\right)} \ \frac{1}{2} \, l {\left(-i \, \sqrt{3} + 1\right)} e^{\left(i \, \alpha\right)} - l e^{\left(i \, b\right)} \ \frac{1}{2} \, l {\left(-i \, \sqrt{3} + 3\right)} e^{\left(i \, \alpha\right)} - l e^{\left(i \, \delta\right)} \end{array}\right) $$
Inverting the matrix in the left hand side yields:
$$ \left(\begin{array}{r} e^{\left(i \, \beta\right)} \ e^{\left(i \, \gamma\right)} \ e^{\left(i \, c\right)} \ e^{\left(i \, d\right)} \ e^{\left(i \, e\right)}
\end{array}\right)
\left(\begin{array}{r} -\frac{l {\left(-i \, \sqrt{3} + 4\right)} e^{\left(i \, \alpha\right)} - 1}{l} \ \frac{2 \, l {\left(-i \, \sqrt{3} + 4\right)} e^{\left(i \, \alpha\right)} - l {\left(-i \, \sqrt{3} - 3\right)} e^{\left(i \, \alpha\right)} - 2 \, l e^{\left(i \, \delta\right)} - 2 i - 2}{2 \, l} \ \frac{2 \, l {\left(-i \, \sqrt{3} + 4\right)} e^{\left(i \, \alpha\right)} + l {\left(-i \, \sqrt{3} + 1\right)} e^{\left(i \, \alpha\right)} - l {\left(-i \, \sqrt{3} - 3\right)} e^{\left(i \, \alpha\right)} + 2 \, l e^{\left(i \, a\right)} - 2 \, l e^{\left(i \, b\right)} - 2 \, l e^{\left(i \, \delta\right)} - 2 i - 2}{2 \, l} \ -\frac{4 \, l {\left(-i \, \sqrt{3} + 4\right)} e^{\left(i \, \alpha\right)} - l {\left(-i \, \sqrt{3} + 3\right)} e^{\left(i \, \alpha\right)} - l {\left(-i \, \sqrt{3} - 3\right)} e^{\left(i \, \alpha\right)} + 2 \, l e^{\left(i \, a\right)} - 2 i - 4}{2 \, l} \ -\frac{2 \, l {\left(-i \, \sqrt{3} + 4\right)} e^{\left(i \, \alpha\right)} - l {\left(-i \, \sqrt{3} + 3\right)} e^{\left(i \, \alpha\right)} + l {\left(-i \, \sqrt{3} + 1\right)} e^{\left(i \, \alpha\right)} - l {\left(-i \, \sqrt{3} - 3\right)} e^{\left(i \, \alpha\right)} + 2 \, l e^{\left(i \, a\right)} - 2 \, l e^{\left(i \, b\right)} - 2 i - 2}{2 \, l} \end{array}\right) $$
This way, we can eliminate the five variables $\beta$, $\gamma$, $c$, $d$ and $e$, by computing the norm of the right hand side and the left hand side. The norms on the left hand side being of course equal to one, which get rids of 5 variables out of 10. We are now left with the 5 following equations:
$$ 0 = -2 \, {\left(\sqrt{3} \sin\left(\alpha\right) + 4 \, \cos\left(\alpha\right)\right)} l + 18 \, l^{2} + 1 \ $$ $$ 0 = {\left({\left(\sqrt{3} \sin\left(\alpha\right) + 11 \, \cos\left(\alpha\right)\right)} \cos\left(\delta\right) - {\left(\sqrt{3} \cos\left(\alpha\right) - 11 \, \sin\left(\alpha\right)\right)} \sin\left(\delta\right) - 31\right)} l^{2} - {\left({\left(\sqrt{3} - 11\right)} \cos\left(\alpha\right) - {\left(\sqrt{3} + 11\right)} \sin\left(\alpha\right) + 2 \, \cos\left(\delta\right) + 2 \, \sin\left(\delta\right)\right)} l - 2\ $$ $$ 0 = {\left(2 \, {\left(\sqrt{3} \sin\left(a\right) - 8 \, \cos\left(a\right)\right)} \cos\left(\alpha\right) - 2 \, {\left(\sqrt{3} \cos\left(a\right) + 8 \, \sin\left(a\right)\right)} \sin\left(\alpha\right) - 67\right)} l^{2} - 2 \, {\left({\left(\sqrt{3} - 16\right)} \cos\left(\alpha\right) - 2 \, {\left(\sqrt{3} + 4\right)} \sin\left(\alpha\right) - 2 \, \cos\left(a\right) - \sin\left(a\right)\right)} l - 5\ $$ $$ 0 = {\left(2 \, {\left(\sqrt{3} \sin\left(a\right) - 6 \, \cos\left(a\right)\right)} \cos\left(\alpha\right) + 2 \, {\left(\sqrt{3} \sin\left(\alpha\right) + \cos\left(a\right) + 6 \, \cos\left(\alpha\right)\right)} \cos\left(b\right) + 2 \, {\left(\sqrt{3} \sin\left(\alpha\right) + \cos\left(a\right) + 6 \, \cos\left(\alpha\right) - \cos\left(b\right)\right)} \cos\left(\delta\right) - 2 \, {\left(\sqrt{3} \cos\left(a\right) + 6 \, \sin\left(a\right)\right)} \sin\left(\alpha\right) - 2 \, {\left(\sqrt{3} \cos\left(\alpha\right) - \sin\left(a\right) - 6 \, \sin\left(\alpha\right)\right)} \sin\left(b\right) - 2 \, {\left(\sqrt{3} \cos\left(\alpha\right) - \sin\left(a\right) - 6 \, \sin\left(\alpha\right) + \sin\left(b\right)\right)} \sin\left(\delta\right) - 41\right)} l^{2} - 2 \, {\left({\left(\sqrt{3} - 6\right)} \cos\left(\alpha\right) - {\left(\sqrt{3} + 6\right)} \sin\left(\alpha\right) - \cos\left(a\right) + \cos\left(b\right) + \cos\left(\delta\right) - \sin\left(a\right) + \sin\left(b\right) + \sin\left(\delta\right)\right)} l - 2\ $$ $$ 0 = {\left({\left(\sqrt{3} \sin\left(a\right) - 9 \, \cos\left(a\right)\right)} \cos\left(\alpha\right) + {\left(\sqrt{3} \sin\left(\alpha\right) + 2 \, \cos\left(a\right) + 9 \, \cos\left(\alpha\right)\right)} \cos\left(b\right) - {\left(\sqrt{3} \cos\left(a\right) + 9 \, \sin\left(a\right)\right)} \sin\left(\alpha\right) - {\left(\sqrt{3} \cos\left(\alpha\right) - 2 \, \sin\left(a\right) - 9 \, \sin\left(\alpha\right)\right)} \sin\left(b\right) - 22\right)} l^{2} - {\left({\left(\sqrt{3} - 9\right)} \cos\left(\alpha\right) - {\left(\sqrt{3} + 9\right)} \sin\left(\alpha\right) - 2 \, \cos\left(a\right) + 2 \, \cos\left(b\right) - 2 \, \sin\left(a\right) + 2 \, \sin\left(b\right)\right)} l - 2\ $$
With the first 3 equations we can linearize any sines and cosines powers of $\alpha$, $\delta$ and $a$. With the last 2 equations we can solve for $cos(b)$ and $sin(b)$ and elimiminate variable $b$ writing $cos(b)^2+sin(b)^2=1$. This yields an polynomial expression in $l$, as well as powers of sines and cosines of 3 the variables $\alpha$, $\delta$ and $a$.
We then proceed to linearize this expression using the first 3 equations in the system until we are only left with an equation that is polynomial in $l$ and linear in $cos(\alpha)$, $cos(a)$ and $cos(\delta)$.
 | 2 | No.2 Revision |
I finally got to a result using a completely different approach.
First I noticed $\rho$ and $\beta$ are one and the same variable as numerical approximative values suggest. That brings down the number of varialbles from 11 to 10. My sincere appologies for not picking that up earlier. Then, rewriting the set of equations as a linear system of the complex field yields
$$ l \left(\begin{array}{rrrrr} 1 & 0 & 0 & 0 & 0 \ -1 & -1 & 0 & 0 & 0 \ -1 & 1 & 0 & 1 & 0 \ -1 & 0 & 0 & 1 & -1 \ 0 & 0 & 1 & 0 & 1 \end{array}\right) \left(\begin{array}{r} e^{\left(i \, \beta\right)} \ e^{\left(i \, \gamma\right)} \ e^{\left(i \, c\right)} \ e^{\left(i \, d\right)} \ e^{\left(i \, e\right)}
\end{array}\right)
\left(\begin{array}{r} -l {\left(-i \, \sqrt{3} + 4\right)} e^{\left(i \, \alpha\right)} + 1 \ \frac{1}{2} \, l {\left(-i \, \sqrt{3} - 3\right)} e^{\left(i \, \alpha\right)} + l e^{\left(i \, \delta\right)} + i \ \frac{1}{2} \, l {\left(-i \, \sqrt{3} + 3\right)} e^{\left(i \, \alpha\right)} - l e^{\left(i \, a\right)} - l e^{\left(i \, \delta\right)} \ \frac{1}{2} \, l {\left(-i \, \sqrt{3} + 1\right)} e^{\left(i \, \alpha\right)} - l e^{\left(i \, b\right)} \ \frac{1}{2} \, l {\left(-i \, \sqrt{3} + 3\right)} e^{\left(i \, \alpha\right)} - l e^{\left(i \, \delta\right)} \end{array}\right) $$
Inverting yields:
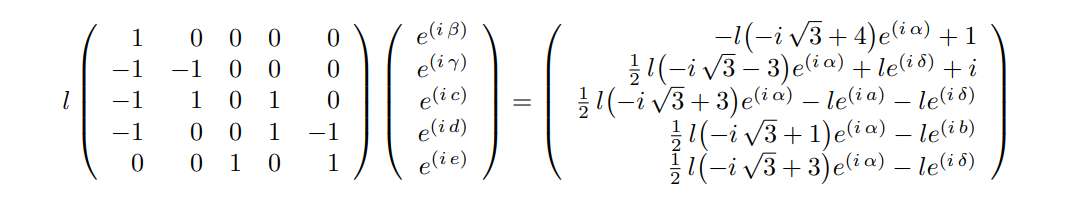
Then, inverting the matrix in the left hand side yields:
$$
\left(\begin{array}{r}
e^{\left(i \, \beta\right)} \
e^{\left(i \, \gamma\right)} \
e^{\left(i \, c\right)} \
e^{\left(i \, d\right)} \
e^{\left(i \, e\right)}
\end{array}\right)
\left(\begin{array}{r}
-\frac{l {\left(-i \, \sqrt{3} + 4\right)} e^{\left(i \, \alpha\right)} - 1}{l} \
\frac{2 \, l {\left(-i \, \sqrt{3} + 4\right)} e^{\left(i \, \alpha\right)} - l {\left(-i \, \sqrt{3} - 3\right)} e^{\left(i \, \alpha\right)} - 2 \, l e^{\left(i \, \delta\right)} - 2 i - 2}{2 \, l} \
\frac{2 \, l {\left(-i \, \sqrt{3} + 4\right)} e^{\left(i \, \alpha\right)} + l {\left(-i \, \sqrt{3} + 1\right)} e^{\left(i \, \alpha\right)} - l {\left(-i \, \sqrt{3} - 3\right)} e^{\left(i \, \alpha\right)} + 2 \, l e^{\left(i \, a\right)} - 2 \, l e^{\left(i \, b\right)} - 2 \, l e^{\left(i \, \delta\right)} - 2 i - 2}{2 \, l} \
-\frac{4 \, l {\left(-i \, \sqrt{3} + 4\right)} e^{\left(i \, \alpha\right)} - l {\left(-i \, \sqrt{3} + 3\right)} e^{\left(i \, \alpha\right)} - l {\left(-i \, \sqrt{3} - 3\right)} e^{\left(i \, \alpha\right)} + 2 \, l e^{\left(i \, a\right)} - 2 i - 4}{2 \, l} \
-\frac{2 \, l {\left(-i \, \sqrt{3} + 4\right)} e^{\left(i \, \alpha\right)} - l {\left(-i \, \sqrt{3} + 3\right)} e^{\left(i \, \alpha\right)} + l {\left(-i \, \sqrt{3} + 1\right)} e^{\left(i \, \alpha\right)} - l {\left(-i \, \sqrt{3} - 3\right)} e^{\left(i \, \alpha\right)} + 2 \, l e^{\left(i \, a\right)} - 2 \, l e^{\left(i \, b\right)} - 2 i - 2}{2 \, l}
\end{array}\right)
$$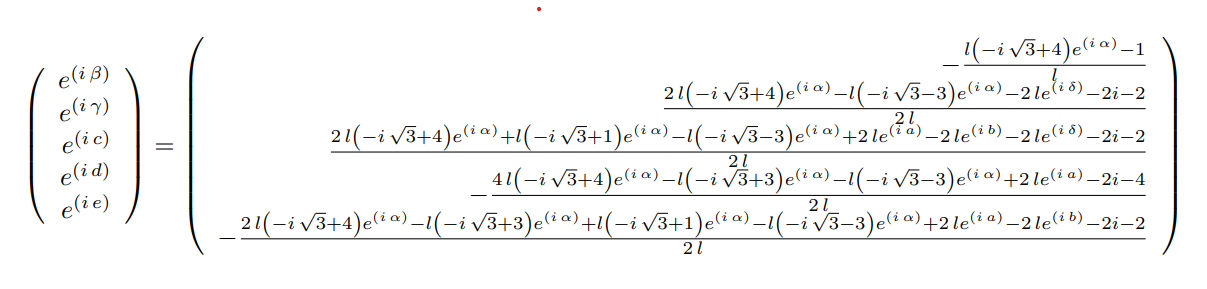
This way, we can eliminate the five variables $\beta$, $\gamma$, $c$, $d$ and $e$, by computing the norm of the right hand side and the left hand side. The norms on the left hand side being of course equal to one, which get rids of 5 variables out of 10. We are now left with the 5 following equations:
$$ 0 = -2 \, {\left(\sqrt{3} \sin\left(\alpha\right) + 4 \, \cos\left(\alpha\right)\right)} l + 18 \, l^{2} + 1 \ $$ $$ 0 = {\left({\left(\sqrt{3} \sin\left(\alpha\right) + 11 \, \cos\left(\alpha\right)\right)} \cos\left(\delta\right) - {\left(\sqrt{3} \cos\left(\alpha\right) - 11 \, \sin\left(\alpha\right)\right)} \sin\left(\delta\right) - 31\right)} l^{2} - {\left({\left(\sqrt{3} - 11\right)} \cos\left(\alpha\right) - {\left(\sqrt{3} + 11\right)} \sin\left(\alpha\right) + 2 \, \cos\left(\delta\right) + 2 \, \sin\left(\delta\right)\right)} l - 2\ $$ $$ 0 = {\left(2 \, {\left(\sqrt{3} \sin\left(a\right) - 8 \, \cos\left(a\right)\right)} \cos\left(\alpha\right) - 2 \, {\left(\sqrt{3} \cos\left(a\right) + 8 \, \sin\left(a\right)\right)} \sin\left(\alpha\right) - 67\right)} l^{2} - 2 \, {\left({\left(\sqrt{3} - 16\right)} \cos\left(\alpha\right) - 2 \, {\left(\sqrt{3} + 4\right)} \sin\left(\alpha\right) - 2 \, \cos\left(a\right) - \sin\left(a\right)\right)} l - 5\ $$ $$ 0 = {\left(2 \, {\left(\sqrt{3} \sin\left(a\right) - 6 \, \cos\left(a\right)\right)} \cos\left(\alpha\right) + 2 \, {\left(\sqrt{3} \sin\left(\alpha\right) + \cos\left(a\right) + 6 \, \cos\left(\alpha\right)\right)} \cos\left(b\right) + 2 \, {\left(\sqrt{3} \sin\left(\alpha\right) + \cos\left(a\right) + 6 \, \cos\left(\alpha\right) - \cos\left(b\right)\right)} \cos\left(\delta\right) - 2 \, {\left(\sqrt{3} \cos\left(a\right) + 6 \, \sin\left(a\right)\right)} \sin\left(\alpha\right) - 2 \, {\left(\sqrt{3} \cos\left(\alpha\right) - \sin\left(a\right) - 6 \, \sin\left(\alpha\right)\right)} \sin\left(b\right) - 2 \, {\left(\sqrt{3} \cos\left(\alpha\right) - \sin\left(a\right) - 6 \, \sin\left(\alpha\right) + \sin\left(b\right)\right)} \sin\left(\delta\right) - 41\right)} l^{2} - 2 \, {\left({\left(\sqrt{3} - 6\right)} \cos\left(\alpha\right) - {\left(\sqrt{3} + 6\right)} \sin\left(\alpha\right) - \cos\left(a\right) + \cos\left(b\right) + \cos\left(\delta\right) - \sin\left(a\right) + \sin\left(b\right) + \sin\left(\delta\right)\right)} l - 2\ $$ $$ 0 = {\left({\left(\sqrt{3} \sin\left(a\right) - 9 \, \cos\left(a\right)\right)} \cos\left(\alpha\right) + {\left(\sqrt{3} \sin\left(\alpha\right) + 2 \, \cos\left(a\right) + 9 \, \cos\left(\alpha\right)\right)} \cos\left(b\right) - {\left(\sqrt{3} \cos\left(a\right) + 9 \, \sin\left(a\right)\right)} \sin\left(\alpha\right) - {\left(\sqrt{3} \cos\left(\alpha\right) - 2 \, \sin\left(a\right) - 9 \, \sin\left(\alpha\right)\right)} \sin\left(b\right) - 22\right)} l^{2} - {\left({\left(\sqrt{3} - 9\right)} \cos\left(\alpha\right) - {\left(\sqrt{3} + 9\right)} \sin\left(\alpha\right) - 2 \, \cos\left(a\right) + 2 \, \cos\left(b\right) - 2 \, \sin\left(a\right) + 2 \, \sin\left(b\right)\right)} l - 2\ $$
With the first 3 equations we can linearize any sines and cosines powers of $\alpha$, $\delta$ and $a$. With the last 2 equations we can solve for $cos(b)$ and $sin(b)$ and elimiminate variable $b$ writing $cos(b)^2+sin(b)^2=1$. This yields an polynomial expression in $l$, as well as powers of sines and cosines of 3 the variables $\alpha$, $\delta$ and $a$.
We then proceed to linearize this expression using the first 3 equations in the system until we are only left with an equation that is polynomial in $l$ and linear in $cos(\alpha)$, $cos(a)$ and $cos(\delta)$.
 | 3 | No.3 Revision |
I finally got to a result using a completely different approach. First I noticed $\rho$ and $\beta$ are one and the same variable as numerical approximative values suggest. That brings down the number of varialbles from 11 to 10. My sincere appologies for not picking that up earlier. Then, rewriting the set of equations as a linear system of the complex field yields:
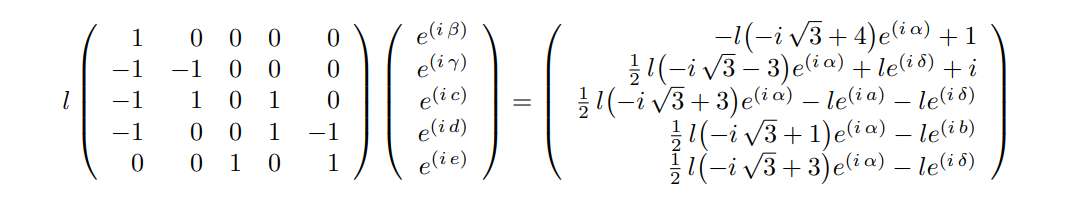
Then, inverting the matrix in the left hand side yields:
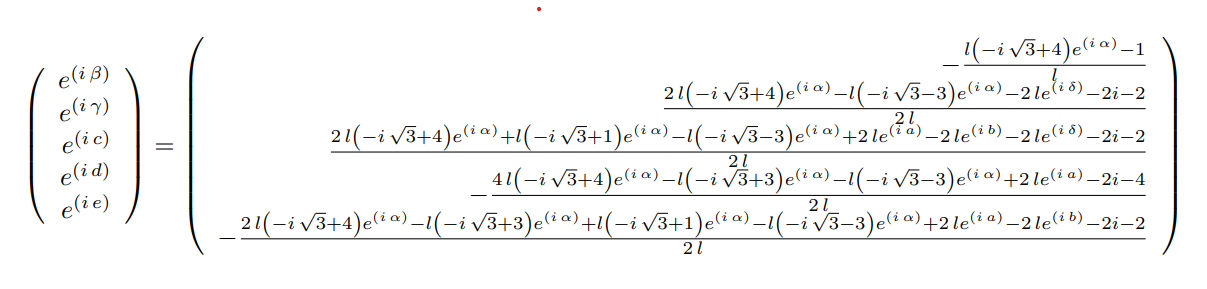
This way, we can eliminate the five variables $\beta$, $\gamma$, $c$, $d$ and $e$, by computing the norm of the right hand side and the left hand side. The norms on the left hand side being of course equal to one, which get rids of 5 variables out of 10. We are now left with the 5 following equations:
$$
$
0 = -2 \, {\left(\sqrt{3} \sin\left(\alpha\right) + 4 \, \cos\left(\alpha\right)\right)} l + 18 \, l^{2} + 1 \
$$
$$
$
$
0 = {\left({\left(\sqrt{3} \sin\left(\alpha\right) + 11 \, \cos\left(\alpha\right)\right)} \cos\left(\delta\right) - {\left(\sqrt{3} \cos\left(\alpha\right) - 11 \, \sin\left(\alpha\right)\right)} \sin\left(\delta\right) - 31\right)} l^{2}
$
$
- {\left({\left(\sqrt{3} - 11\right)} \cos\left(\alpha\right) - {\left(\sqrt{3} + 11\right)} \sin\left(\alpha\right) + 2 \, \cos\left(\delta\right) + 2 \, \sin\left(\delta\right)\right)} l - 2\
$$
$$
2
$
$
0 = {\left(2 \, {\left(\sqrt{3} \sin\left(a\right) - 8 \, \cos\left(a\right)\right)} \cos\left(\alpha\right) - 2 \, {\left(\sqrt{3} \cos\left(a\right) + 8 \, \sin\left(a\right)\right)} \sin\left(\alpha\right) - 67\right)} l^{2} - 2 \,
$
$ - 2 {\left({\left(\sqrt{3} - 16\right)} \cos\left(\alpha\right) - 2 \, {\left(\sqrt{3} + 4\right)} \sin\left(\alpha\right) - 2 \, \cos\left(a\right) - \sin\left(a\right)\right)} l - 5\
$$
$$
5
$
$
0 = {\left(2 \, {\left(\sqrt{3} \sin\left(a\right) - 6 \, {\left({\left(\sqrt{3} \sin\left(a\right) - 9 \cos\left(a\right)\right)} \cos\left(\alpha\right) + 2 \, {\left(\sqrt{3} \sin\left(\alpha\right) + \cos\left(a\right) + 6 \,
$
$
+ {\left(\sqrt{3} \sin\left(\alpha\right) + 2 \cos\left(a\right) + 9 \cos\left(\alpha\right)\right)} \cos\left(b\right)
- {\left(\sqrt{3} \cos\left(a\right) + 9 \sin\left(a\right)\right)} \sin\left(\alpha\right) - {\left(\sqrt{3} \cos\left(\alpha\right) - 2 \sin\left(a\right) - 9 \sin\left(\alpha\right)\right)} \sin\left(b\right) - 22\right)} l^{2}
$
$
- {\left({\left(\sqrt{3} - 9\right)} \cos\left(\alpha\right) - {\left(\sqrt{3} + 9\right)} \sin\left(\alpha\right) - 2 \cos\left(a\right) + 2 \cos\left(b\right) - 2 \sin\left(a\right) + 2 \, {\left(\sqrt{3} \sin\left(\alpha\right) + \cos\left(a\right) + \sin\left(b\right)\right)} l - 2
$
$
0 = \left(2 {\left(\sqrt{3} \sin\left(a\right) - 6 \, \cos\left(a\right)\right)} \cos\left(\alpha\right) + 2 {\left(\sqrt{3} \sin\left(\alpha\right) + \cos\left(a\right) + 6 \cos\left(\alpha\right)\right)} \cos\left(b\right) + 2 {\left(\sqrt{3} \sin\left(\alpha\right) + \cos\left(a\right) + 6 \cos\left(\alpha\right) - \cos\left(b\right)\right)} \cos\left(\delta\right) - 2 \, {\left(\sqrt{3} \cos\left(a\right) + 6 \, \sin\left(a\right)\right)} \sin\left(\alpha\right) - 2 \, {\left(\sqrt{3} \cos\left(\alpha\right) - \sin\left(a\right) - 6 \, \sin\left(\alpha\right)\right)} \sin\left(b\right) - 2 \, {\left(\sqrt{3} \cos\left(\alpha\right) - \sin\left(a\right) - 6 \, \sin\left(\alpha\right) + \sin\left(b\right)\right)} \sin\left(\delta\right) - 41\right)} l^{2} - 2 \, {\left({\left(\sqrt{3} - 6\right)} \cos\left(\alpha\right) - {\left(\sqrt{3} + 6\right)} \sin\left(\alpha\right) - \cos\left(a\right) + \cos\left(b\right) + \cos\left(\delta\right) - \sin\left(a\right) + \sin\left(b\right) + \sin\left(\delta\right)\right)} l - 2\
$$
$$
0 = {\left({\left(\sqrt{3} \sin\left(a\right) - 9 \, \cos\left(a\right)\right)} \cos\left(\alpha\right) + {\left(\sqrt{3} \sin\left(\alpha\right) + 2 \, \cos\left(a\right) + 9 \, \cos\left(\alpha\right)\right)} \cos\left(b\right) - {\left(\sqrt{3} \cos\left(a\right) + 9 \, \sin\left(a\right)\right)} \sin\left(\alpha\right) - {\left(\sqrt{3} \cos\left(\alpha\right) - 2 \, \sin\left(a\right) - 9 \, \sin\left(\alpha\right)\right)} \sin\left(b\right) - 22\right)} l^{2} - {\left({\left(\sqrt{3} - 9\right)} \cos\left(\alpha\right) - {\left(\sqrt{3} + 9\right)} \sin\left(\alpha\right) - 2 \, \cos\left(a\right) + 2 \, \cos\left(b\right) - 2 \, \sin\left(a\right) + 2 \, \sin\left(b\right)\right)} l - 2\
$$2
$
With the first 3 equations we can linearize any sines and cosines powers of $\alpha$, $\delta$ and $a$. With the last 2 equations we can solve for $cos(b)$ and $sin(b)$ and elimiminate variable $b$ writing $cos(b)^2+sin(b)^2=1$. This yields an polynomial expression in $l$, as well as powers of sines and cosines of 3 the variables $\alpha$, $\delta$ and $a$.
We then proceed to linearize this expression using the first 3 equations in the system until we are only left with an equation that is polynomial in $l$ and linear in $cos(\alpha)$, $cos(a)$ and $cos(\delta)$.
 | 4 | No.4 Revision |
I finally got to a result using a completely different approach. First I noticed $\rho$ and $\beta$ are one and the same variable as numerical approximative values suggest. That brings down the number of varialbles from 11 to 10. My sincere appologies for not picking that up earlier. Then, rewriting the set of equations as a linear system of the complex field yields:
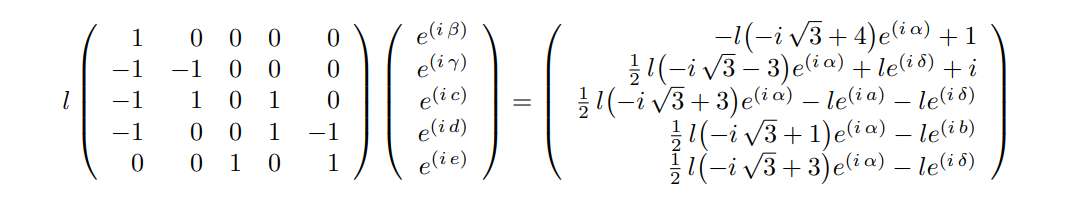
Then, inverting the matrix in the left hand side yields:
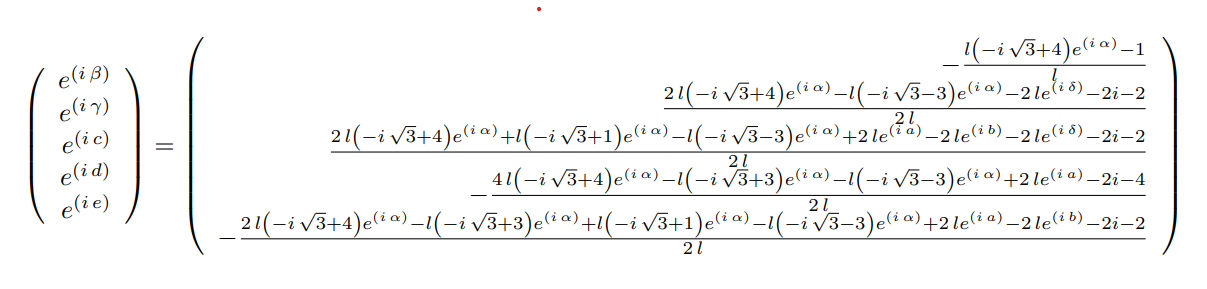
This way, we can eliminate the five variables $\beta$, $\gamma$, $c$, $d$ and $e$, by computing the norm of the right hand side and the left hand side. The norms on the left hand side being of course equal to one, which get rids of 5 variables out of 10. We are now left with the 5 following equations:
$
0 = -2 {\left(\sqrt{3} \sin\left(\alpha\right) + 4 \cos\left(\alpha\right)\right)} l + 18 l^{2} + 1 \
$
$ 0 = {\left({\left(\sqrt{3} \sin\left(\alpha\right) + 11 \cos\left(\alpha\right)\right)} \cos\left(\delta\right) - {\left(\sqrt{3} \cos\left(\alpha\right) - 11 \sin\left(\alpha\right)\right)} \sin\left(\delta\right) - 31\right)} l^{2} $ $ - {\left({\left(\sqrt{3} - 11\right)} \cos\left(\alpha\right) - {\left(\sqrt{3} + 11\right)} \sin\left(\alpha\right) + 2 \cos\left(\delta\right) + 2 \sin\left(\delta\right)\right)} l - 2 $
$ 0 = {\left(2 {\left(\sqrt{3} \sin\left(a\right) - 8 \cos\left(a\right)\right)} \cos\left(\alpha\right) - 2 {\left(\sqrt{3} \cos\left(a\right) + 8 \sin\left(a\right)\right)} \sin\left(\alpha\right) - 67\right)} l^{2} $ $ - 2 {\left({\left(\sqrt{3} - 16\right)} \cos\left(\alpha\right) - 2 {\left(\sqrt{3} + 4\right)} \sin\left(\alpha\right) - 2 \cos\left(a\right) - \sin\left(a\right)\right)} l - 5 $
$ 0 = {\left({\left(\sqrt{3} \sin\left(a\right) - 9 \cos\left(a\right)\right)} \cos\left(\alpha\right) $ $ + {\left(\sqrt{3} \sin\left(\alpha\right) + 2 \cos\left(a\right) + 9 \cos\left(\alpha\right)\right)} \cos\left(b\right) - {\left(\sqrt{3} \cos\left(a\right) + 9 \sin\left(a\right)\right)} \sin\left(\alpha\right) - {\left(\sqrt{3} \cos\left(\alpha\right) - 2 \sin\left(a\right) - 9 \sin\left(\alpha\right)\right)} \sin\left(b\right) - 22\right)} l^{2} $ $ - {\left({\left(\sqrt{3} - 9\right)} \cos\left(\alpha\right) - {\left(\sqrt{3} + 9\right)} \sin\left(\alpha\right) - 2 \cos\left(a\right) + 2 \cos\left(b\right) - 2 \sin\left(a\right) + 2 \, \sin\left(b\right)\right)} l - 2 $
$
0 = \left(2 {\left(\sqrt{3} \sin\left(a\right) - 6 \cos\left(a\right)\right)} \cos\left(\alpha\right) + 2 {\left(\sqrt{3} \sin\left(\alpha\right) + \cos\left(a\right) + 6 \cos\left(\alpha\right)\right)} \cos\left(b\right) + 2 {\left(\sqrt{3} \sin\left(\alpha\right) + \cos\left(a\right) + 6 \cos\left(\alpha\right) - \cos\left(b\right)\right)} \cos\left(\delta\right) - 2 {\left(\sqrt{3} \cos\left(a\right) + 6 \, \sin\left(a\right)\right)} \sin\left(\alpha\right) - 2 {\left(\sqrt{3} \cos\left(\alpha\right) - \sin\left(a\right) - 6 \sin\left(\alpha\right)\right)} \sin\left(b\right) - 2 {\left(\sqrt{3} \cos\left(\alpha\right) - \sin\left(a\right) - 6 \sin\left(\alpha\right) + \sin\left(b\right)\right)} \sin\left(\delta\right) - 41\right)} l^{2} - 2 {\left({\left(\sqrt{3} - 6\right)} \cos\left(\alpha\right) - {\left(\sqrt{3} + 6\right)} \sin\left(\alpha\right) - \cos\left(a\right) + \cos\left(b\right) + \cos\left(\delta\right) - \sin\left(a\right) + \sin\left(b\right) + \sin\left(\delta\right)\right)} l - 2
$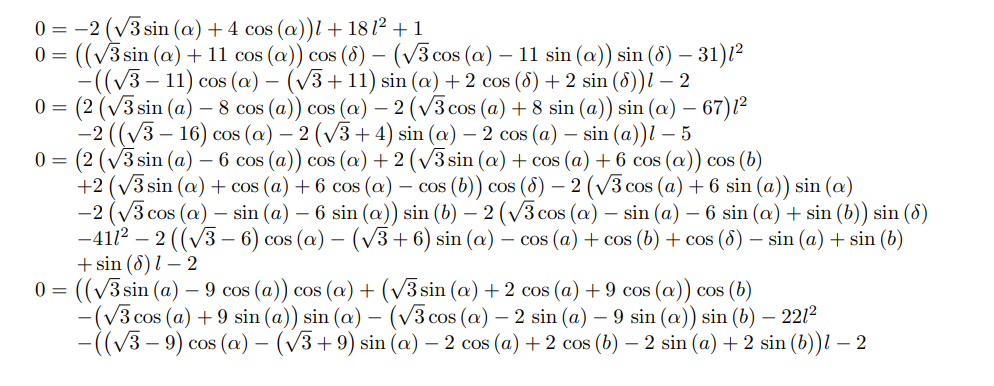
With the first 3 equations we can linearize any sines and cosines powers of $\alpha$, $\delta$ and $a$. With the last 2 equations we can solve for $cos(b)$ and $sin(b)$ and elimiminate variable $b$ writing $cos(b)^2+sin(b)^2=1$. This yields an polynomial expression in $l$, as well as powers of sines and cosines of 3 the variables $\alpha$, $\delta$ and $a$.
We then proceed to linearize this expression using the first 3 equations in the system until we are only left with an equation that is polynomial in $l$ and linear in $cos(\alpha)$, $cos(a)$ and $cos(\delta)$.
 | 5 | No.5 Revision |
I finally got to a result using a completely different approach. First I noticed $\rho$ and $\beta$ are one and the same variable as numerical approximative values suggest. That brings down the number of varialbles from 11 to 10. My sincere appologies for not picking that up earlier. Then, rewriting the set of equations as a linear system of the complex field yields:
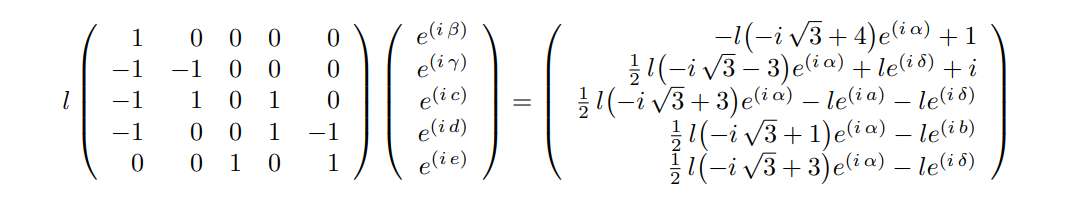
Then, inverting the matrix in the left hand side yields:
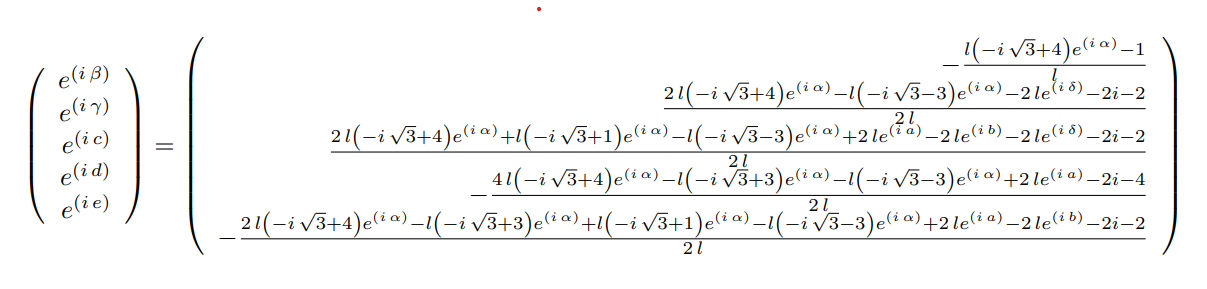
This way, we can eliminate the five variables $\beta$, $\gamma$, $c$, $d$ and $e$, by computing the norm of the right hand side and the left hand side. The norms on the left hand side being of course equal to one, which get rids of 5 variables out of 10. We are now left with the 5 following equations:
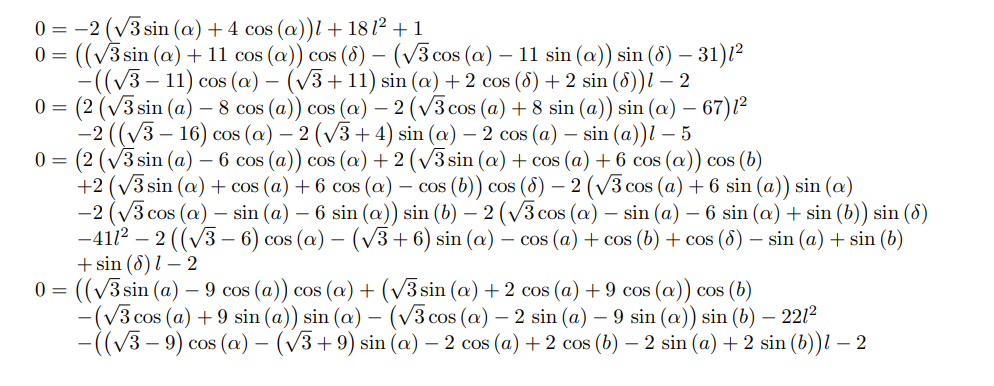
With the first 3 equations we can linearize any sines and cosines powers of $\alpha$, $\delta$ and $a$. With the last 2 equations we can solve for $cos(b)$ and $sin(b)$ and elimiminate variable $b$ writing $cos(b)^2+sin(b)^2=1$. This yields an polynomial expression in $l$, as well as powers of sines and cosines of 3 the variables $\alpha$, $\delta$ and $a$.
We then proceed to linearize this expression using the first 3 equations in the system until we are only left with an equation that is polynomial in $l$ and linear in $cos(\alpha)$, $cos(a)$ and $cos(\delta)$.
Since the expression is linear in $cos(\delta)$, we solve for $cos(\delta)$ and substitute into equation (2). This leaves us with a rational equation in $cos(a)$ and $cos(\alpha)$, which we linearize just as earlier in order to obtain a linear equation in $cos(a)$ and $cos(\alpha)$.
We repeat that process in order to eliminate $cos(a)$ and $cos(\alpha)$.
As a result, we obtain a 136 degree polynomial in $l$, for which our numerical l value is a root.
The result is accessible in the following Permalink:
 | 6 | No.6 Revision |
I finally got to a result using a completely different approach. First I noticed $\rho$ and $\beta$ are one and the same variable as numerical approximative values suggest. That brings down the number of varialbles from 11 to 10. My sincere appologies for not picking that up earlier. Then, rewriting the set of equations as a linear system of the complex field yields:
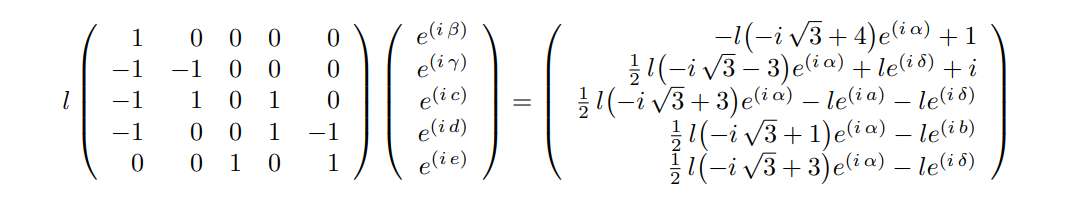
Then, inverting the matrix in the left hand side yields:
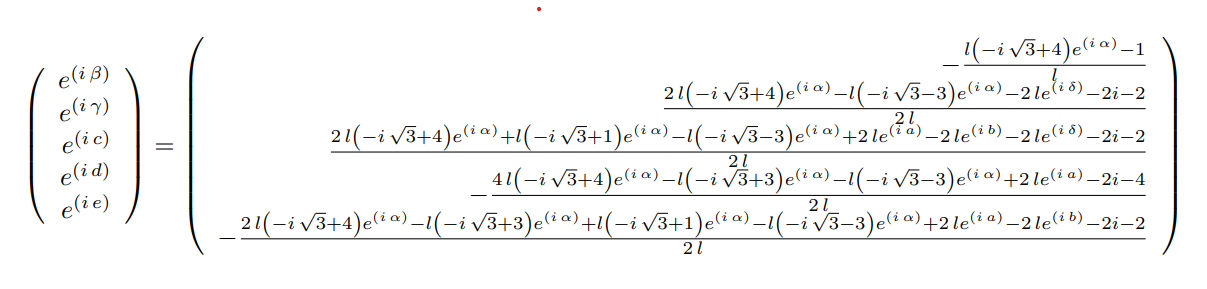
This way, we can eliminate the five variables $\beta$, $\gamma$, $c$, $d$ and $e$, by computing the norm of the right hand side and the left hand side. The norms on the left hand side being of course equal to one, which get rids of 5 variables out of 10. We are now left with the 5 following equations:
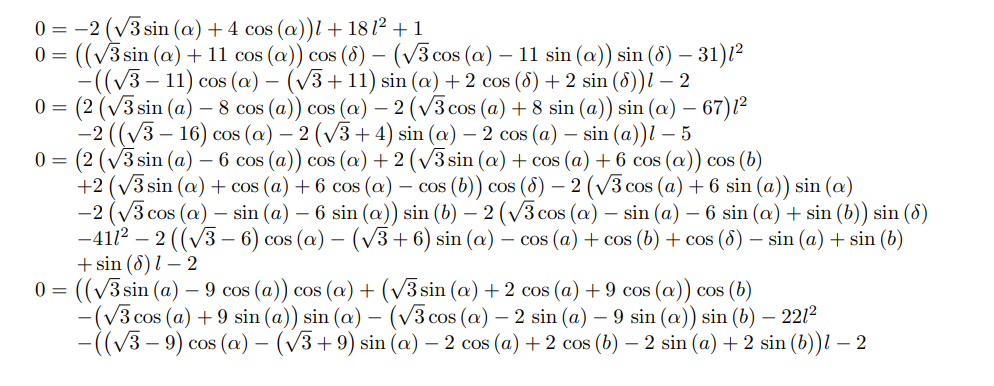
With the first 3 equations we can linearize any sines and cosines powers of $\alpha$, $\delta$ and $a$. With the last 2 equations we can solve for $cos(b)$ and $sin(b)$ and elimiminate variable $b$ writing $cos(b)^2+sin(b)^2=1$. This yields an polynomial expression in $l$, as well as powers of sines and cosines of 3 the variables $\alpha$, $\delta$ and $a$.
We then proceed to linearize this expression using the first 3 equations in the system until we are only left with an equation that is polynomial in $l$ and linear in $cos(\alpha)$, $cos(a)$ and $cos(\delta)$.
Since the expression is linear in $cos(\delta)$, we solve for $cos(\delta)$ and substitute into equation (2). This leaves us with a rational equation in $cos(a)$ and $cos(\alpha)$, which we linearize just as earlier in order to obtain a linear equation in $cos(a)$ and $cos(\alpha)$.
We repeat that process in order to eliminate $cos(a)$ and $cos(\alpha)$.
As a result, we obtain a 136 degree polynomial in $l$, for which our numerical l value is a root.
The result is accessible in the following Permalink:
We still have a final question though... Can we be absolutely certain that this is the minimum polynomial for $l$? Or could we still factor out a smaller degree minimum polynomial?
Thanks for your help!!
 | 7 | No.7 Revision |
I finally got to a result using a completely different approach.
First I noticed $\rho$ and $\beta$ are one and the same variable as numerical approximative values suggest. That brings down the number of varialbles from 11 to 10. My sincere appologies for not picking that up earlier. Then, rewriting the set of equations as a linear system of over the complex field yields:
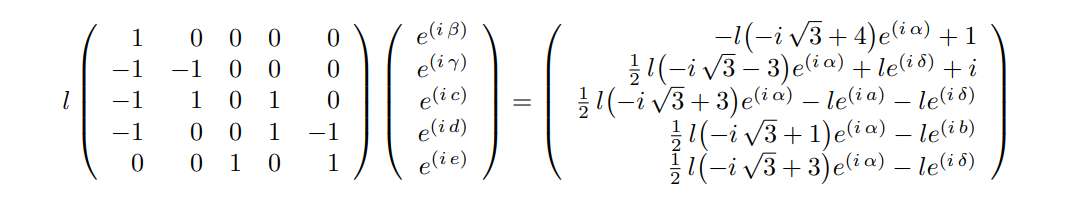
Then, inverting the matrix in the left hand side yields:
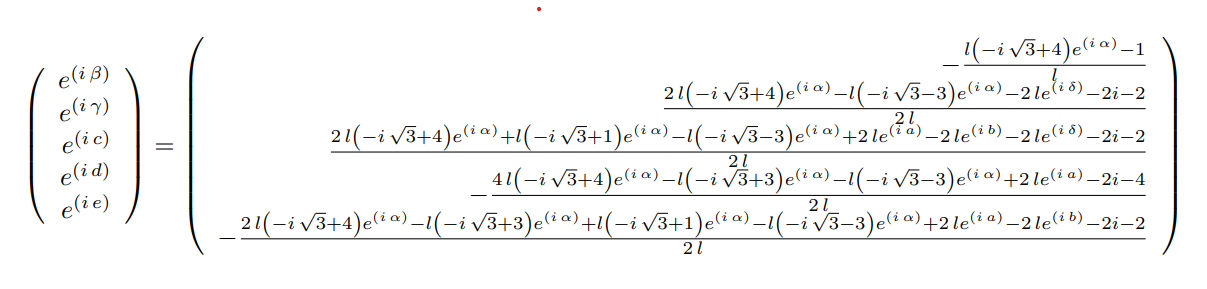
This way, we can eliminate the five variables $\beta$, $\gamma$, $c$, $d$ and $e$, by computing the norm of the right hand side and the left hand side. The norms on the left hand side being of course equal to one, which get rids of 5 variables out of 10. We are now left with the 5 following equations:
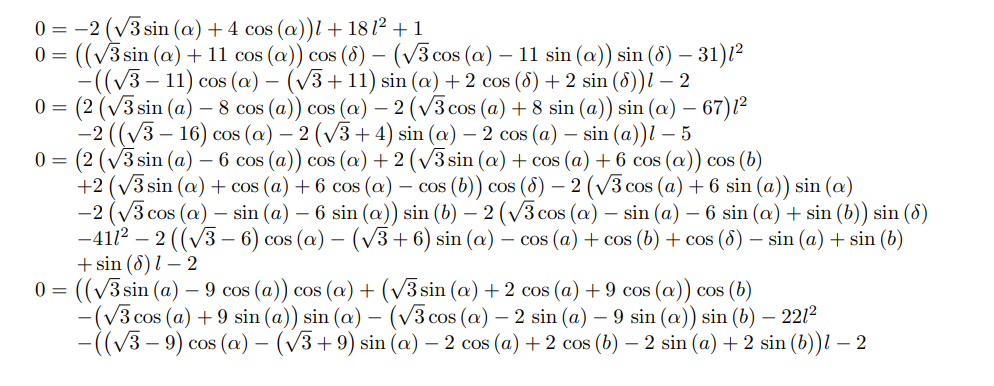
With the first 3 equations we can linearize any sines and cosines powers of $\alpha$, $\delta$ and $a$. With the last 2 equations we can solve for $cos(b)$ and $sin(b)$ and elimiminate variable $b$ writing $cos(b)^2+sin(b)^2=1$. This yields an polynomial expression in $l$, as well as powers of sines and cosines of 3 the variables $\alpha$, $\delta$ and $a$.
We then proceed to linearize this expression using the first 3 equations in the system until we are only left with an equation that is polynomial in $l$ and linear in $cos(\alpha)$, $cos(a)$ and $cos(\delta)$.
Since the expression is linear in $cos(\delta)$, we solve for $cos(\delta)$ and substitute into equation (2). This leaves us with a rational equation in $cos(a)$ and $cos(\alpha)$, which we linearize just as earlier in order to obtain a linear equation in $cos(a)$ and $cos(\alpha)$.
We repeat that process in order to eliminate $cos(a)$ and $cos(\alpha)$.
As a result, we obtain a 136 degree polynomial in $l$, for which our numerical l value is a root.
The result is accessible in the following Permalink:
We still have a final question though... Can we be absolutely certain that this is the minimum polynomial for $l$? Or could we still factor out a smaller degree minimum polynomial?
Thanks for your help!!
 | 8 | No.8 Revision |
I finally got to a result using a completely different approach. First I noticed $\rho$ and $\beta$ are one and the same variable as numerical approximative values suggest. That brings down the number of varialbles from 11 to 10. My sincere appologies for not picking that up earlier. Then, rewriting the set of equations as a linear system over the complex field yields:
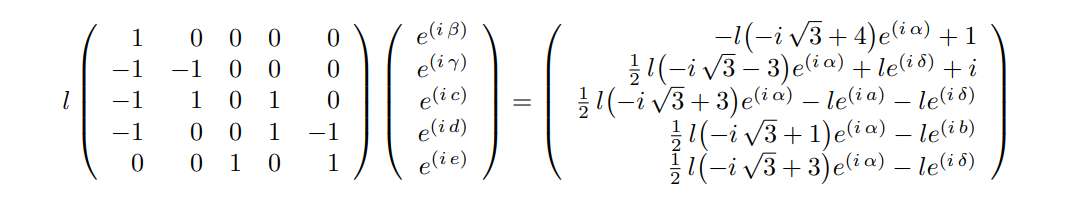
Then, inverting the matrix in the left hand side yields:
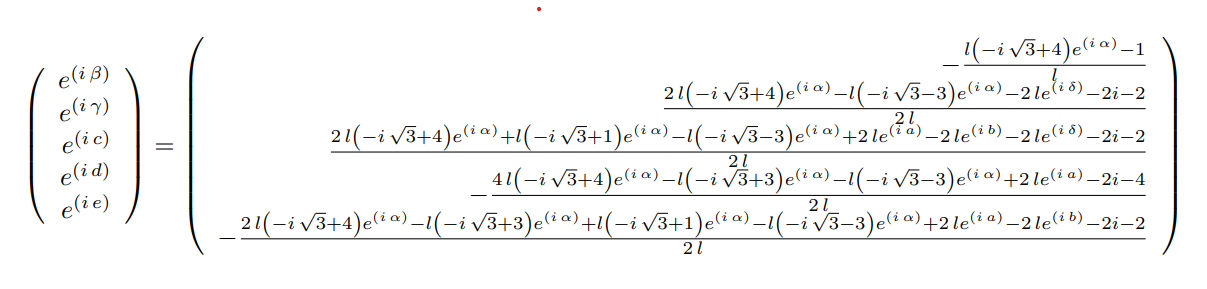
This way, we can eliminate the five variables $\beta$, $\gamma$, $c$, $d$ and $e$, by computing the norm of the right hand side and the left hand side. The norms on the left hand side being of course equal to one, which get rids of 5 variables out of 10. We are now left with the 5 following equations:equations, of the 5 variables $l, \alpha, \delta, a and b$:
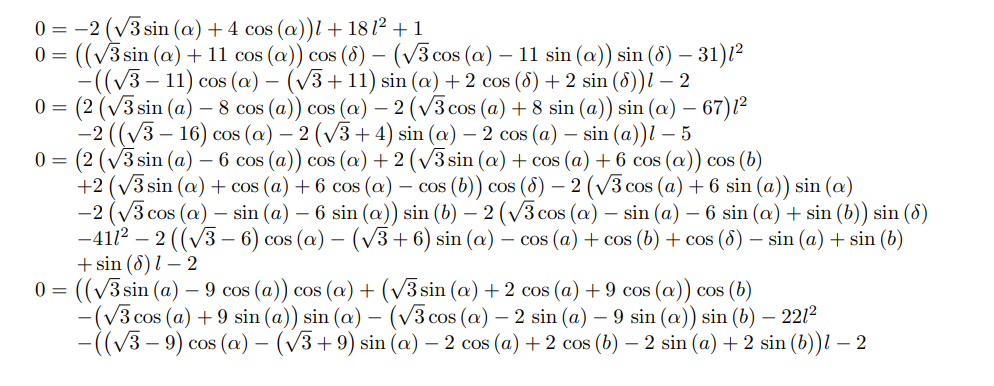
With the first 3 equations we can linearize any sines and cosines powers of $\alpha$, $\delta$ and $a$. With the last 2 equations we can solve for $cos(b)$ and $sin(b)$ and elimiminate variable $b$ writing $cos(b)^2+sin(b)^2=1$. This yields an polynomial expression in $l$, as well as powers of sines and cosines of 3 the variables $\alpha$, $\delta$ and $a$.
We then proceed to linearize this expression using the first 3 equations in the system until we are only left with an equation that is polynomial in $l$ and linear in $cos(\alpha)$, $cos(a)$ and $cos(\delta)$.
Since the expression is linear in $cos(\delta)$, we solve for $cos(\delta)$ and substitute into equation (2). This leaves us with a rational equation in $cos(a)$ and $cos(\alpha)$, which we linearize just as earlier in order to obtain a linear equation in $cos(a)$ and $cos(\alpha)$.
We repeat that process in order to eliminate $cos(a)$ and $cos(\alpha)$.
As a result, we obtain a 136 degree polynomial in $l$, for which our numerical l value is a root.
The result is accessible in the following Permalink:
We still have a final question though... Can we be absolutely certain that this is the minimum polynomial for $l$? Or could we still factor out a smaller degree minimum polynomial?
Thanks for your help!!
 | 9 | No.9 Revision |
I finally got to a result using a completely different approach. First I noticed $\rho$ and $\beta$ are one and the same variable as numerical approximative values suggest. That brings down the number of varialbles from 11 to 10. My sincere appologies for not picking that up earlier. Then, rewriting the set of equations as a linear system over the complex field yields:
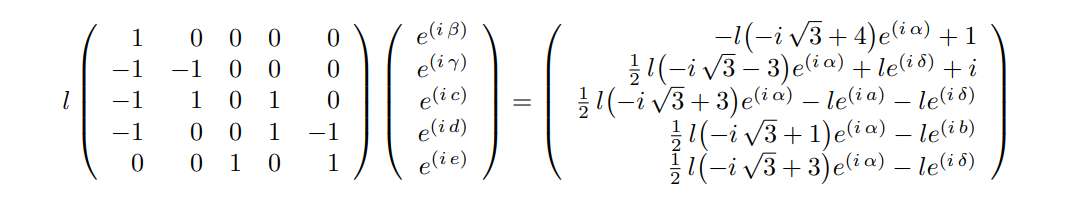
Then, inverting the matrix in the left hand side yields:
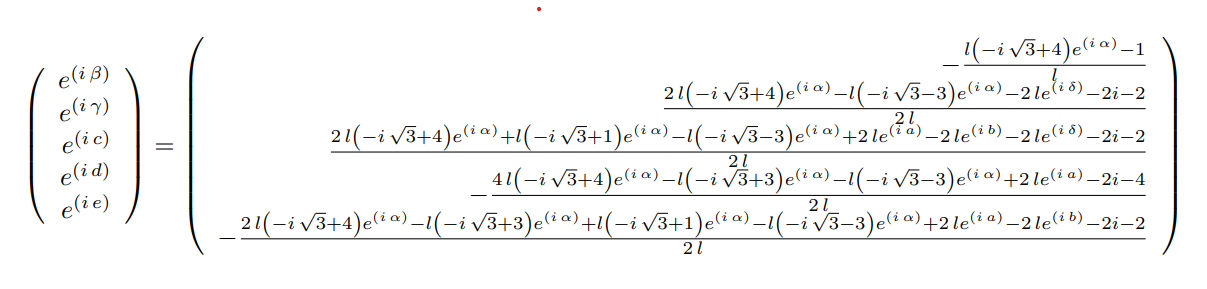
This way, we can eliminate the five variables $\beta$, $\gamma$, $c$, $d$ and $e$, by computing the norm of the right hand side and the left hand side. The norms on the left hand side being of course equal to one, which get rids of 5 variables out of 10. We are now left with the 5 following equations, of the 5 variables $l, \alpha, \delta, a and b$:a$ and $b$:
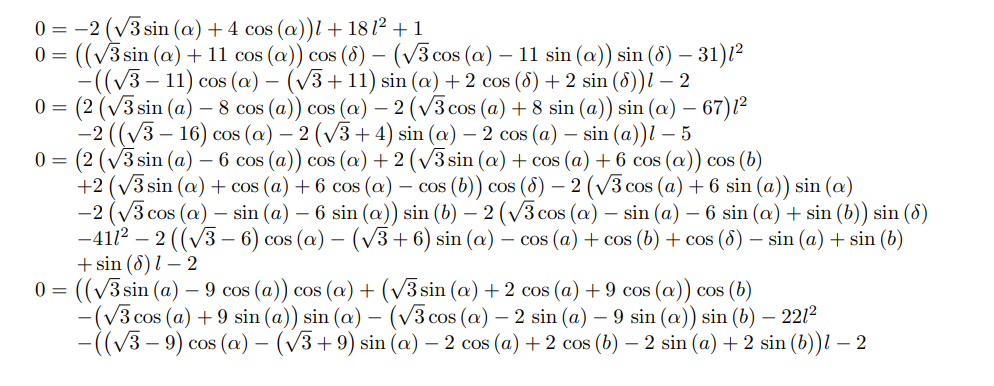
With the first 3 equations we can linearize any sines and cosines powers of $\alpha$, $\delta$ and $a$. With the last 2 equations we can solve for $cos(b)$ and $sin(b)$ and elimiminate variable $b$ writing $cos(b)^2+sin(b)^2=1$. This yields an polynomial expression in $l$, as well as powers of sines and cosines of 3 the variables $\alpha$, $\delta$ and $a$.
We then proceed to linearize this expression using the first 3 equations in the system until we are only left with an equation that is polynomial in $l$ and linear in $cos(\alpha)$, $cos(a)$ and $cos(\delta)$.
Since the expression is linear in $cos(\delta)$, we solve for $cos(\delta)$ and substitute into equation (2). This leaves us with a rational equation in $cos(a)$ and $cos(\alpha)$, which we linearize just as earlier in order to obtain a linear equation in $cos(a)$ and $cos(\alpha)$.
We repeat that process in order to eliminate $cos(a)$ and $cos(\alpha)$.
As a result, we obtain a 136 degree polynomial in $l$, for which our numerical l value is a root.
The result is accessible in the following Permalink:
We still have a final question though... Can we be absolutely certain that this is the minimum polynomial for $l$? Or could we still factor out a smaller degree minimum polynomial?
Thanks for your help!!
 | 10 | No.10 Revision |
I finally got to a result using a completely different approach. First I noticed $\rho$ and $\beta$ are one and the same variable as numerical approximative values suggest. That brings down the number of varialbles from 11 to 10. My sincere appologies for not picking that up earlier. Then, rewriting the set of equations as a linear system over the complex field yields:
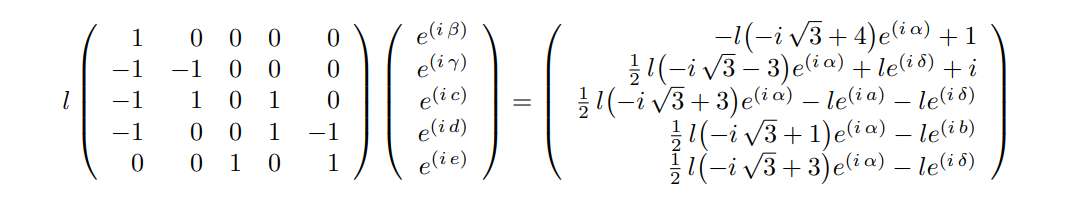
Then, inverting the matrix in the left hand side yields:
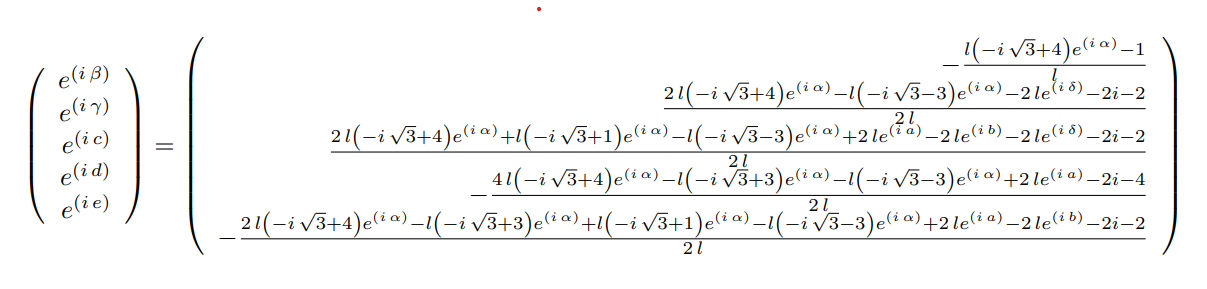
This way, we can eliminate the five variables $\beta$, $\gamma$, $c$, $d$ and $e$, by computing the norm of the right hand side and the left hand side. The norms on the left hand side being of course equal to one, which get rids of 5 variables out of 10. We are now left with the 5 following equations, of the 5 variables $l, \alpha, \delta, a$ and $b$:
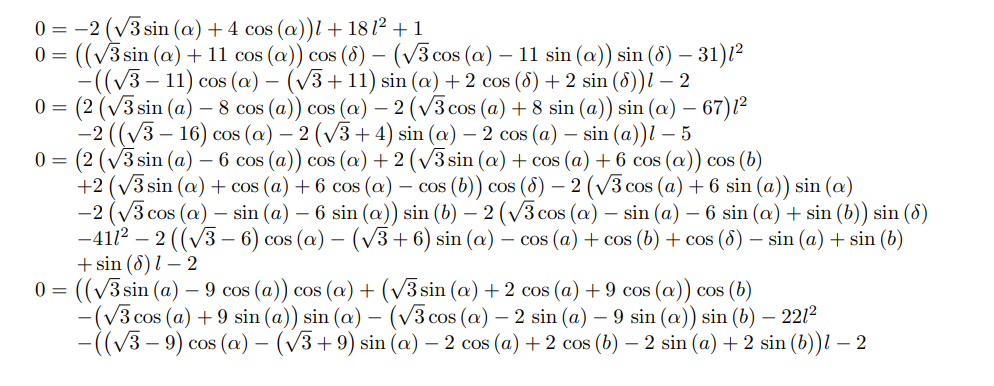
At this point, I tried to use Groebner elimination hoping that having less variables would make it possible to solver before timeout. However, this did not succeed so I went for a different approach.
With the first 3 equations we can linearize any sines and cosines powers of $\alpha$, $\delta$ and $a$. With the last 2 equations we can solve for $cos(b)$ and $sin(b)$ and elimiminate variable $b$ writing $cos(b)^2+sin(b)^2=1$. This yields an polynomial expression in $l$, as well as powers of sines and cosines of 3 the variables $\alpha$, $\delta$ and $a$.
We then proceed to linearize this expression using the first 3 equations in the system until we are only left with an equation that is polynomial in $l$ and linear in $cos(\alpha)$, $cos(a)$ and $cos(\delta)$.
Since the expression is linear in $cos(\delta)$, we solve for $cos(\delta)$ and substitute into equation (2). This leaves us with a rational equation in $cos(a)$ and $cos(\alpha)$, which we linearize just as earlier in order to obtain a linear equation in $cos(a)$ and $cos(\alpha)$.
We repeat that process in order to eliminate $cos(a)$ and $cos(\alpha)$.
As a result, we obtain a 136 degree polynomial in $l$, for which our numerical l value is a root.
The result is accessible in the following Permalink:
We still have a final question though... Can we be absolutely certain that this is the minimum polynomial for $l$? Or could we still factor out a smaller degree minimum polynomial?
Thanks for your help!!
 | 11 | No.11 Revision |
I finally got to a result using a completely different approach. First I noticed $\rho$ and $\beta$ are one and the same variable as numerical approximative values suggest. That brings down the number of varialbles from 11 to 10. My sincere appologies for not picking that up earlier. Then, rewriting the set of equations as a linear system over the complex field yields:
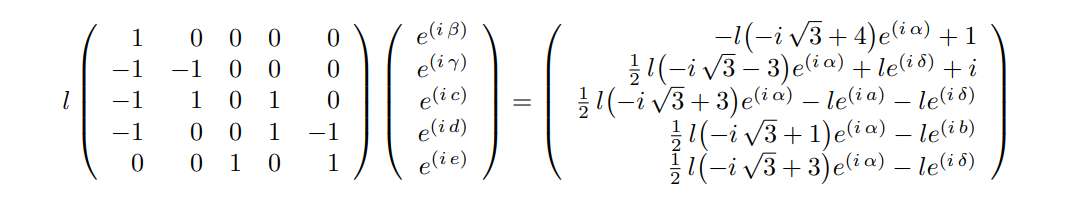
Then, inverting the matrix in the left hand side yields:
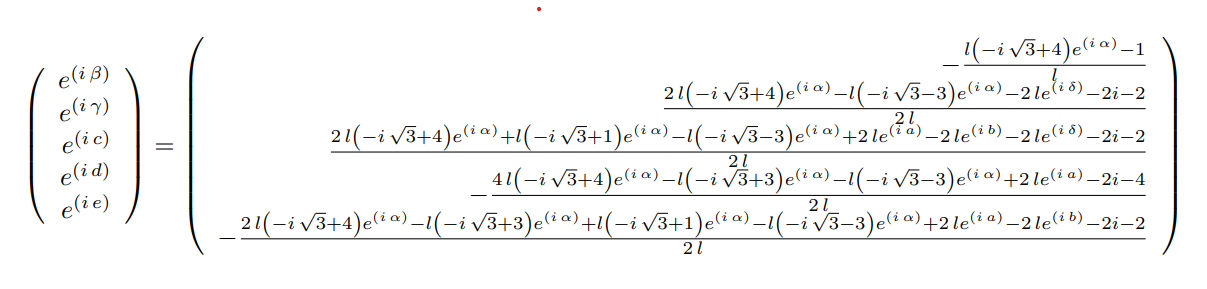
This way, we can eliminate the five variables $\beta$, $\gamma$, $c$, $d$ and $e$, by computing the norm of the right hand side and the left hand side. The norms on the left hand side being of course equal to one, which get rids gets rid of 5 variables out of 10. We are now left with the 5 following equations, equations of the 5 variables $l, \alpha, \delta, a$ and $b$:
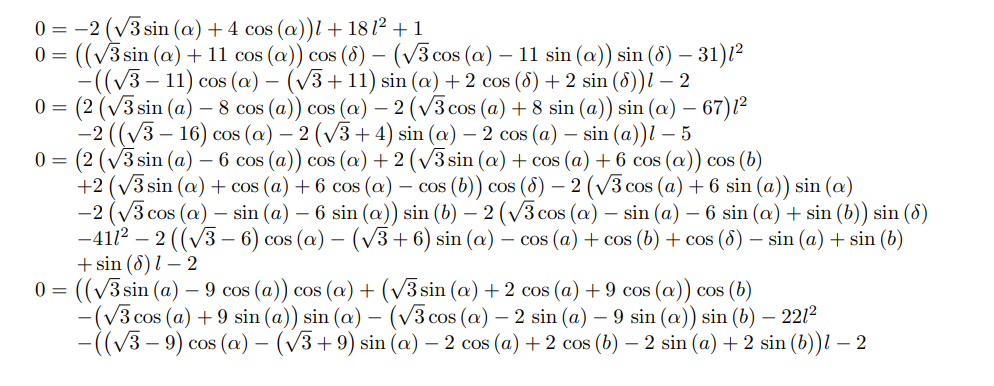
At this point, I tried to use Groebner elimination hoping that having less variables would make it possible to solver solve before timeout. However, this did not succeed so I went for a different approach.
With the first 3 equations we can linearize any sines and cosines powers of $\alpha$, $\delta$ and $a$.
With the last 2 equations we can solve for $cos(b)$ and $sin(b)$ $\cos(b)$ and $\sin(b)$ and elimiminate variable $b$ writing $cos(b)^2+sin(b)^2=1$. $\cos(b)^2+\sin(b)^2=1$. This yields an polynomial expression in $l$, as well as powers of sines and cosines of 3 the variables $\alpha$, $\delta$ and $a$.
We then proceed to linearize this expression using the first 3 equations in the system until we are only left with an equation that is polynomial in $l$ and linear in $cos(\alpha)$, $cos(a)$ and $cos(\delta)$.
Since the expression is linear in $cos(\delta)$, we solve for $cos(\delta)$ and substitute into equation (2). This leaves us with a rational equation in $cos(a)$ and $cos(\alpha)$, which we linearize just as earlier in order to obtain a linear equation in $cos(a)$ and $cos(\alpha)$.
We repeat that process in order to eliminate $cos(a)$ and $cos(\alpha)$.
As a result, we obtain a 136 degree polynomial in $l$, for which our numerical l value is a root.
The result is accessible in the following Permalink:
We still have a final question though... Can we be absolutely certain that this is the minimum polynomial for $l$? Or could we still factor out a smaller degree minimum polynomial?
Thanks for your help!!
 | 12 | No.12 Revision |
I finally got to a result using a completely different approach. First I noticed $\rho$ and $\beta$ are one and the same variable as numerical approximative values suggest. That brings down the number of varialbles from 11 to 10. My sincere appologies for not picking that up earlier. Then, rewriting the set of equations as a linear system over the complex field yields:
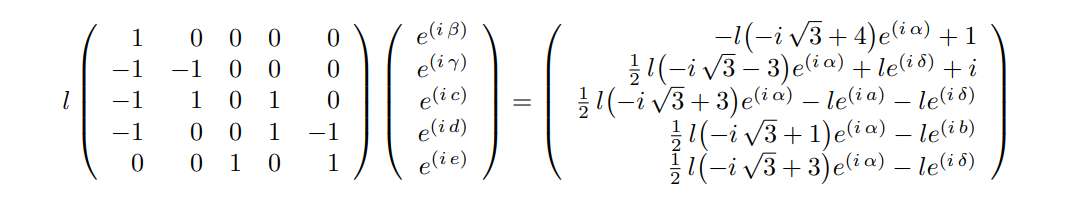
Then, inverting the matrix in the left hand side yields:
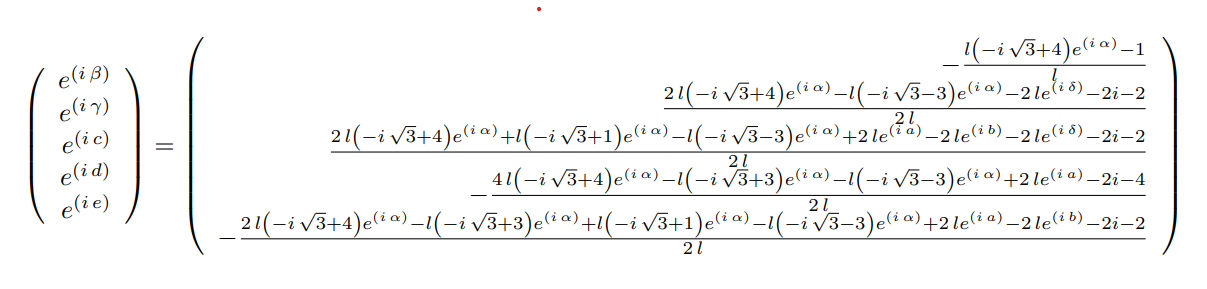
This way, we can eliminate the five variables $\beta$, $\gamma$, $c$, $d$ and $e$, by computing the norm of the right hand side and the left hand side. The norms on the left hand side being of course equal to one, which gets rid of 5 variables out of 10. We are now left with 5 equations of the 5 variables $l, \alpha, \delta, a$ and $b$:
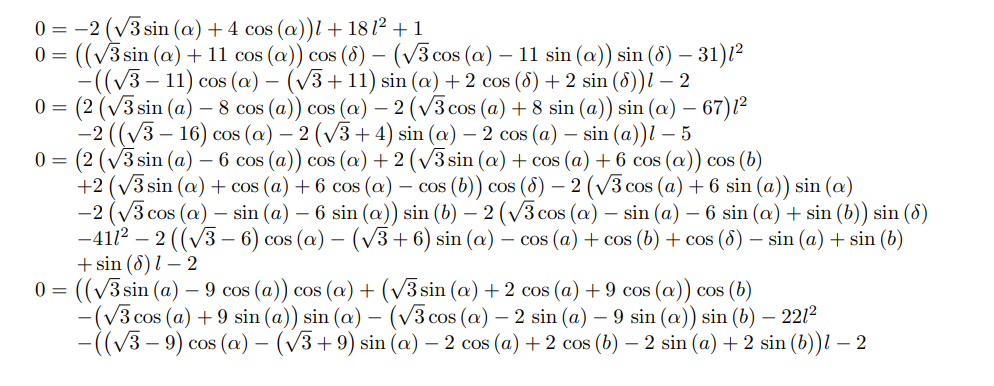
At this point, I tried to use Groebner elimination hoping that having less variables would make it possible to solve before timeout. However, this did not succeed so I went for a different approach.
With the first 3 equations we can linearize any sines and cosines powers of $\alpha$, $\delta$ and $a$.
With the last 2 equations we can solve for $\cos(b)$ and $\sin(b)$ and elimiminate variable $b$ writing $\cos(b)^2+\sin(b)^2=1$. This yields an a polynomial expression in $l$, as well as powers of sines and cosines of the variables $\alpha$, $\delta$ and $a$.
We then proceed to linearize this expression using the first 3 equations in the system until we are only left with an equation that is polynomial in $l$ and linear in $cos(\alpha)$, $cos(a)$ and $cos(\delta)$.
Since the expression is linear in $cos(\delta)$, we solve for $cos(\delta)$ and substitute into equation (2). This leaves us with a rational equation in $cos(a)$ and $cos(\alpha)$, which we linearize just as earlier in order to obtain a linear equation in $cos(a)$ and $cos(\alpha)$.
We repeat that process in order to eliminate $cos(a)$ and $cos(\alpha)$.
As a result, we obtain a 136 degree polynomial in $l$, for which our numerical l value is a root.
The result is accessible in the following Permalink:
We still have a final question though... Can we be absolutely certain that this is the minimum polynomial for $l$? Or could we still factor out a smaller degree minimum polynomial?
Thanks for your help!!
 | 13 | No.13 Revision |
I finally got to a result using a completely different approach. First I noticed $\rho$ and $\beta$ are one and the same variable as numerical approximative values suggest. That brings down the number of varialbles from 11 to 10. My sincere appologies for not picking that up earlier. Then, rewriting the set of equations as a linear system over the complex field yields:
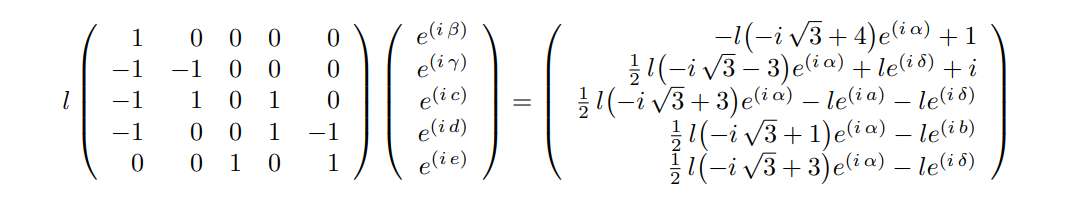
Then, inverting the matrix in the left hand side yields:
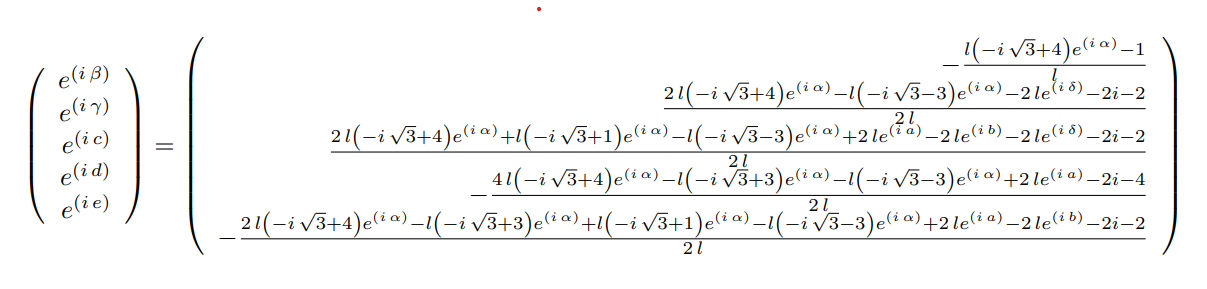
This way, we can eliminate the five variables $\beta$, $\gamma$, $c$, $d$ and $e$, by computing the norm norms of the right hand side sides and the left hand side. sides. The norms on the left hand side being sides are of course equal to one, which gets rid of 5 variables out of 10. We are now left with 5 equations of the 5 variables $l, \alpha, \delta, a$ and $b$:
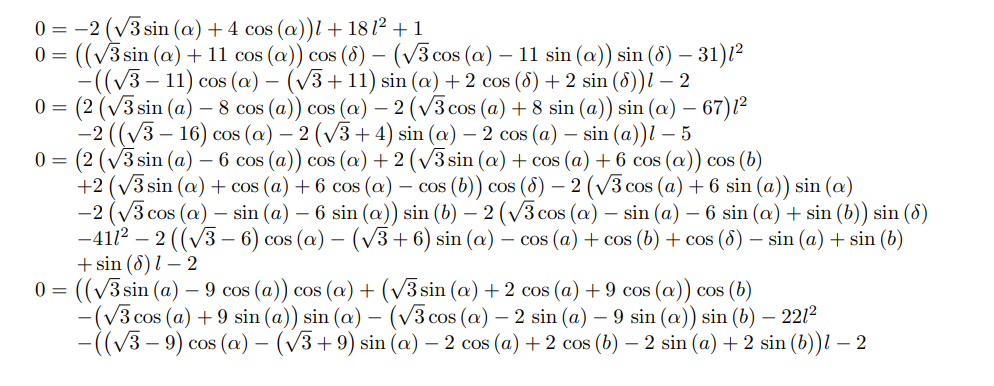
At this point, I tried to use Groebner elimination hoping that having less variables would make it possible to solve before timeout. However, this did not succeed so I went for a different approach.
With the first 3 equations we can linearize any sines and cosines powers of $\alpha$, $\delta$ and $a$. With the last 2 equations we can solve for $\cos(b)$ and $\sin(b)$ and elimiminate variable $b$ writing $\cos(b)^2+\sin(b)^2=1$. This yields a polynomial expression in $l$, as well as powers of sines and cosines of the variables $\alpha$, $\delta$ and $a$.
We then proceed to linearize this expression using the first 3 equations in the system until we are only left with an equation that is polynomial in $l$ and linear in $cos(\alpha)$, $cos(a)$ and $cos(\delta)$.
Since the expression is linear in $cos(\delta)$, we solve for $cos(\delta)$ and substitute into equation (2). This leaves us with a rational equation in $cos(a)$ and $cos(\alpha)$, which we linearize just as earlier in order to obtain a linear equation in $cos(a)$ and $cos(\alpha)$.
We repeat that process in order to eliminate $cos(a)$ and $cos(\alpha)$.
As a result, we obtain a 136 degree polynomial in $l$, for which our numerical l value is a root.
The result is accessible in the following Permalink:
We still have a final question though... Can we be absolutely certain that this is the minimum polynomial for $l$? Or could we still factor out a smaller degree minimum polynomial?
Thanks for your help!!
