Revision history [back]
 | 1 | initial version |
sage: var("z, u")
(z, u)
sage: Ex=3*z^2/(2-12*z^2+sqrt(1 - 12*z^2))-u
sage: %time Sol0=solve(Ex, z)
CPU times: user 1.47 s, sys: 146 ms, total: 1.62 s
Wall time: 1.59 s
sage: Sol0
[z == -sqrt(1/3)*sqrt((sqrt(-12*z^2 + 1)*u + 2*u)/(4*u + 1)), z == sqrt(1/3)*sqrt((sqrt(-12*z^2 + 1)*u + 2*u)/(4*u + 1))]
Your equation has a rational fraction with radicals of a polynomial in your variableof interest. Sage's default solver is unable to solve it, and returns a (set of) equation(s) equivalent to the original one (an implicit solution) :
Let's try a variant of Maxima's solver (see solve? for details) :
sage: %time Sol1=solve(Ex, z, to_poly_solve=True)
CPU times: user 2min 15s, sys: 959 ms, total: 2min 16s
Wall time: 1min 35s
sage: Sol1
[z == -sqrt(1/3)*sqrt((sqrt(-12*z^2 + 1)*u + 2*u)/(4*u + 1)),
z == sqrt(1/3)*sqrt((sqrt(-12*z^2 + 1)*u + 2*u)/(4*u + 1))]
Takes its sweet time, and returns the same (non-)solution.
Force the use of the alternate algorithm :
sage: %time Sol2=solve(Ex, z, to_poly_solve="force")
CPU times: user 30.9 s, sys: 243 ms, total: 31.1 s
Wall time: 21.8 s
sage: Sol2
[]
SOL...
Let's get rid of the radicals, by squaring the equations until there is no radical. It can be done manually, or you can a Sympy utility for this :
sage: from sympy.solvers.solvers import unrad
sage: foo=unrad(Ex._sympy_()) ; foo
(48*u**2*z**4 - 12*u**2*z**2 + u**2 + 24*u*z**4 - 4*u*z**2 + 3*z**4, [])
foo[0] is a (Sympy) polynomial in u and z whose roots are a superset of those of Ex (see unrad? for details).
We can try to solve it for z to get a set of candidate solutions (by squaring, we may have introduced spurious solutions...) :
sage: %time CSol=solve(foo[0]._sage_(), z) ; CSol
CPU times: user 15.2 ms, sys: 0 ns, total: 15.2 ms
Wall time: 15.2 ms
[z == -sqrt(2*u^2 + 1/3*sqrt(-12*u^2 + 1)*u + 2/3*u)/(4*u + 1), z == sqrt(2*u^2 + 1/3*sqrt(-12*u^2 + 1)*u + 2/3*u)/(4*u + 1), z == -sqrt(2*u^2 - 1/3*sqrt(-12*u^2 + 1)*u + 2/3*u)/(4*u + 1), z == sqrt(2*u^2 - 1/3*sqrt(-12*u^2 + 1)*u + 2/3*u)/(4*u + 1)]
However, filtering the "real" solutions isn't easy ,: Sage is currently unable to check those candidate solutions :
sage: [Ex.subs(s).is_zero() for s in CSol]
[False, False, False, False]
This filtering may be possible by numerical checks in a "likely" region of u values. Rapid checks for u in the [-5, 5] real interval found no valid solution.
Using Sympy directly returns a set of possible implicit solutions :
sage: solve(Ex, z, algorithm="sympy")
Complement(ConditionSet(z, Eq(u/3 + z**2/(12*z**2 - sqrt(1 - 12*z**2) - 2), 0), {-sqrt(6*u**2/(48*u**2 + 24*u + 3) - u*sqrt(1 - 12*u**2)/(48*u**2 + 24*u + 3) + 2*u/(48*u**2 + 24*u + 3)), sqrt(6*u**2/(48*u**2 + 24*u + 3) - u*sqrt(1 - 12*u**2)/(48*u**2 + 24*u + 3) + 2*u/(48*u**2 + 24*u + 3)), -sqrt(6*u**2/(48*u**2 + 24*u + 3) + u*sqrt(1 - 12*u**2)/(48*u**2 + 24*u + 3) + 2*u/(48*u**2 + 24*u + 3)), sqrt(6*u**2/(48*u**2 + 24*u + 3) + u*sqrt(1 - 12*u**2)/(48*u**2 + 24*u + 3) + 2*u/(48*u**2 + 24*u + 3))}), ConditionSet(z, Eq(12*z**2 - sqrt(1 - 12*z**2) - 2, 0), {-sqrt(2)*3**(1/4)/8 - sqrt(2)*3**(3/4)/24 + I*(-sqrt(2)*3**(1/4)/8 + sqrt(2)*3**(3/4)/24), -sqrt(2)*3**(1/4)/8 - sqrt(2)*3**(3/4)/24 + I*(-sqrt(2)*3**(3/4)/24 + sqrt(2)*3**(1/4)/8), sqrt(2)*3**(3/4)/24 + sqrt(2)*3**(1/4)/8 + I*(-sqrt(2)*3**(1/4)/8 + sqrt(2)*3**(3/4)/24), sqrt(2)*3**(3/4)/24 + sqrt(2)*3**(1/4)/8 + I*(-sqrt(2)*3**(3/4)/24 + sqrt(2)*3**(1/4)/8)}))
which is no more checkable than the previous ones...
Querying "the competition" (Mathematica) via WolframAlpha may be instructive. My first attempts do not make me optimist...
Sorry not to be more helpful.
 | 2 | No.2 Revision |
Your equation has a rational fraction with radicals of a polynomial in your variableof interest. Sage's default solver is unable to solve it, and returns a (set of) equation(s) equivalent to the original one (an implicit solution) :
Let's try a variant of Maxima's solver (see solve? for details) :
sage: %time Sol1=solve(Ex, z, to_poly_solve=True)
CPU times: user 2min 15s, sys: 959 ms, total: 2min 16s
Wall time: 1min 35s
sage: Sol1
[z == -sqrt(1/3)*sqrt((sqrt(-12*z^2 + 1)*u + 2*u)/(4*u + 1)),
z == sqrt(1/3)*sqrt((sqrt(-12*z^2 + 1)*u + 2*u)/(4*u + 1))]
Takes its sweet time, and returns the same (non-)solution.
Force the use of the alternate algorithm :
sage: %time Sol2=solve(Ex, z, to_poly_solve="force")
CPU times: user 30.9 s, sys: 243 ms, total: 31.1 s
Wall time: 21.8 s
sage: Sol2
[]
SOL...
Let's get rid of the radicals, by squaring the equations until there is no radical. It can be done manually, or you can a Sympy utility for this :
sage: from sympy.solvers.solvers import unrad
sage: foo=unrad(Ex._sympy_()) ; foo
(48*u**2*z**4 - 12*u**2*z**2 + u**2 + 24*u*z**4 - 4*u*z**2 + 3*z**4, [])
foo[0] is a (Sympy) polynomial in u and z whose roots are a superset of those of Ex (see unrad? for details).
We can try to solve it for z to get a set of candidate solutions (by squaring, we may have introduced spurious solutions...) :
sage: %time CSol=solve(foo[0]._sage_(), z) ; CSol
CPU times: user 15.2 ms, sys: 0 ns, total: 15.2 ms
Wall time: 15.2 ms
[z == -sqrt(2*u^2 + 1/3*sqrt(-12*u^2 + 1)*u + 2/3*u)/(4*u + 1), z == sqrt(2*u^2 + 1/3*sqrt(-12*u^2 + 1)*u + 2/3*u)/(4*u + 1), z == -sqrt(2*u^2 - 1/3*sqrt(-12*u^2 + 1)*u + 2/3*u)/(4*u + 1), z == sqrt(2*u^2 - 1/3*sqrt(-12*u^2 + 1)*u + 2/3*u)/(4*u + 1)]
However, filtering the "real" solutions isn't easy ,: Sage is currently unable to check those candidate solutions :
sage: [Ex.subs(s).is_zero() for s in CSol]
[False, False, False, False]
This filtering may be possible by numerical checks in a "likely" region of u values. Rapid checks for u in the [-5, 5] real interval found no valid solution.
Using Sympy directly returns a set of possible implicit solutions :
sage: solve(Ex, z, algorithm="sympy")
Complement(ConditionSet(z, Eq(u/3 + z**2/(12*z**2 - sqrt(1 - 12*z**2) - 2), 0), {-sqrt(6*u**2/(48*u**2 + 24*u + 3) - u*sqrt(1 - 12*u**2)/(48*u**2 + 24*u + 3) + 2*u/(48*u**2 + 24*u + 3)), sqrt(6*u**2/(48*u**2 + 24*u + 3) - u*sqrt(1 - 12*u**2)/(48*u**2 + 24*u + 3) + 2*u/(48*u**2 + 24*u + 3)), -sqrt(6*u**2/(48*u**2 + 24*u + 3) + u*sqrt(1 - 12*u**2)/(48*u**2 + 24*u + 3) + 2*u/(48*u**2 + 24*u + 3)), sqrt(6*u**2/(48*u**2 + 24*u + 3) + u*sqrt(1 - 12*u**2)/(48*u**2 + 24*u + 3) + 2*u/(48*u**2 + 24*u + 3))}), ConditionSet(z, Eq(12*z**2 - sqrt(1 - 12*z**2) - 2, 0), {-sqrt(2)*3**(1/4)/8 - sqrt(2)*3**(3/4)/24 + I*(-sqrt(2)*3**(1/4)/8 + sqrt(2)*3**(3/4)/24), -sqrt(2)*3**(1/4)/8 - sqrt(2)*3**(3/4)/24 + I*(-sqrt(2)*3**(3/4)/24 + sqrt(2)*3**(1/4)/8), sqrt(2)*3**(3/4)/24 + sqrt(2)*3**(1/4)/8 + I*(-sqrt(2)*3**(1/4)/8 + sqrt(2)*3**(3/4)/24), sqrt(2)*3**(3/4)/24 + sqrt(2)*3**(1/4)/8 + I*(-sqrt(2)*3**(3/4)/24 + sqrt(2)*3**(1/4)/8)}))
which is no more checkable than the previous ones...
Querying "the competition" (Mathematica) via WolframAlpha may be instructive. My first attempts do not make me optimist...
EDIT : A bit of numerical check leads me to think that the first two solutions are valid ain a small region of the Argand plane around 0 :
sage: graphics_array([[complex_plot(Ex.subs(CSol[2*t+v]).function(u), (-1, 1), (-1, 1), plot_points=200) for v in range(2)] for t in range(2)])
Launched png viewer for Graphics Array of size 2 x 2
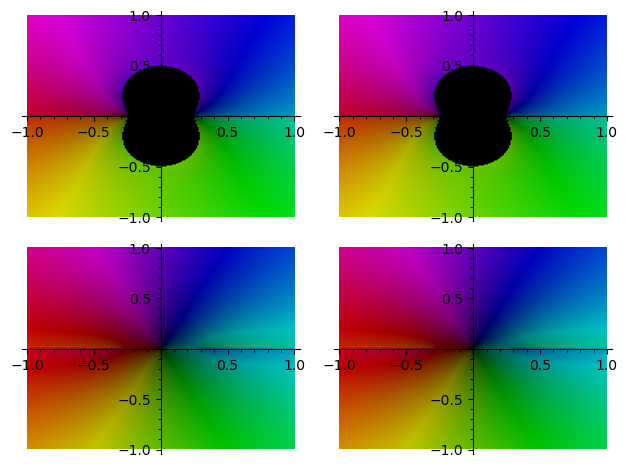
I have (currently) no idea of the reason of this region of validity. Someone with better knowledge of the behaviour of the (complex) rational fractions is welcome to explain it...
Sorry not to be more helpful.
 | 3 | No.3 Revision |
sage: var("z, Naive approach:
sage: z, u = SR.var("z, u")
(z, u)
sage: Ex=3z^2/(2-12z^2+sqrt(1 - 12z^2))-u
sage: Ex = 3*z^2 / (2 - 12*z^2 + sqrt(1 - 12*z^2)) - u
sage: %time Sol0=solve(Ex, Sol0 = solve(Ex, z)
CPU times: user 1.47 s, sys: 146 ms, total: 1.62 s
Wall time: 1.59 s
sage: Sol0
[z == -sqrt(1/3)sqrt((sqrt(-12z^2 + 1)u + 2u)/(4u + 1)), -sqrt(1/3)*sqrt((sqrt(-12*z^2 + 1)*u + 2*u)/(4*u + 1)),
z == sqrt(1/3)sqrt((sqrt(-12z^2 + 1)u + 2u)/(4*u + 1))]sqrt(1/3)*sqrt((sqrt(-12*z^2 + 1)*u + 2*u)/(4*u + 1))]
Your equation has a rational fraction function with radicals of a polynomial in your variableof variable of interest. Sage's default solver is unable to solve it, and returns a (set of) equation(s) equivalent to the original one (an implicit solution) :
Let's try a variant of Maxima's solver (see solve? for details) :details):
sage: %time Sol1=solve(Ex, Sol1 = solve(Ex, z, to_poly_solve=True)
CPU times: user 2min 15s, sys: 959 ms, total: 2min 16s
Wall time: 1min 35s
sage: Sol1
[z == -sqrt(1/3)*sqrt((sqrt(-12*z^2 + 1)*u + 2*u)/(4*u + 1)),
z == sqrt(1/3)*sqrt((sqrt(-12*z^2 + 1)*u + 2*u)/(4*u + 1))]
Takes its sweet time, and returns the same (non-)solution.
Force the use of the alternate algorithm :
sage: %time Sol2=solve(Ex, Sol2 = solve(Ex, z, to_poly_solve="force")
CPU times: user 30.9 s, sys: 243 ms, total: 31.1 s
Wall time: 21.8 s
sage: Sol2
[]
SOL...
Let's get rid of the radicals, by squaring the equations until there is no radical. It can be done manually, or you can a Sympy utility for this :this:
sage: from sympy.solvers.solvers import unrad
sage: foo=unrad(Ex._sympy_()) ; foo = unrad(Ex._sympy_())
sage: foo
(48*u**2*z**4 - 12*u**2*z**2 + u**2 + 24*u*z**4 - 4*u*z**2 + 3*z**4, [])
foo[0] is a (Sympy) polynomial in u and z whose roots are a superset of those of Ex (see unrad? for details).
We can try to solve it for z to get a set of candidate solutions (by squaring, we may have introduced spurious solutions...) :
sage: %time CSol=solve(foo[0]._sage_(), z) ; CSol = solve(foo[0]._sage_(), z); CSol
CPU times: user 15.2 ms, sys: 0 ns, total: 15.2 ms
Wall time: 15.2 ms
[z == -sqrt(2*u^2 + 1/3*sqrt(-12*u^2 + 1)*u + 2/3*u)/(4*u + 1), 1),
z == sqrt(2*u^2 + 1/3*sqrt(-12*u^2 + 1)*u + 2/3*u)/(4*u + 1), 1),
z == -sqrt(2*u^2 - 1/3*sqrt(-12*u^2 + 1)*u + 2/3*u)/(4*u + 1), 1),
z == sqrt(2*u^2 - 1/3*sqrt(-12*u^2 + 1)*u + 2/3*u)/(4*u + 1)]
However, filtering the "real" solutions isn't easy ,: easy: Sage is currently unable to check those candidate solutions :solutions:
sage: [Ex.subs(s).is_zero() for s in CSol]
[False, False, False, False]
This filtering may be possible by numerical checks in a "likely" region of u values. Rapid checks for u in the [-5, 5] real interval found no valid solution.
Using Sympy directly returns a set of possible implicit solutions :solutions:
sage: solve(Ex, z, algorithm="sympy")
Complement(ConditionSet(z, Eq(u/3 + z**2/(12*z**2 - sqrt(1 - 12*z**2) - 2), 0), {-sqrt(6*u**2/(48*u**2 + 24*u + 3) - u*sqrt(1 - 12*u**2)/(48*u**2 + 24*u + 3) + 2*u/(48*u**2 + 24*u + 3)), sqrt(6*u**2/(48*u**2 + 24*u + 3) - u*sqrt(1 - 12*u**2)/(48*u**2 + 24*u + 3) + 2*u/(48*u**2 + 24*u + 3)), -sqrt(6*u**2/(48*u**2 + 24*u + 3) + u*sqrt(1 - 12*u**2)/(48*u**2 + 24*u + 3) + 2*u/(48*u**2 + 24*u + 3)), sqrt(6*u**2/(48*u**2 + 24*u + 3) + u*sqrt(1 - 12*u**2)/(48*u**2 + 24*u + 3) + 2*u/(48*u**2 + 24*u + 3))}), ConditionSet(z, Eq(12*z**2 - sqrt(1 - 12*z**2) - 2, 0), {-sqrt(2)*3**(1/4)/8 - sqrt(2)*3**(3/4)/24 + I*(-sqrt(2)*3**(1/4)/8 + sqrt(2)*3**(3/4)/24), -sqrt(2)*3**(1/4)/8 - sqrt(2)*3**(3/4)/24 + I*(-sqrt(2)*3**(3/4)/24 + sqrt(2)*3**(1/4)/8), sqrt(2)*3**(3/4)/24 + sqrt(2)*3**(1/4)/8 + I*(-sqrt(2)*3**(1/4)/8 + sqrt(2)*3**(3/4)/24), sqrt(2)*3**(3/4)/24 + sqrt(2)*3**(1/4)/8 + I*(-sqrt(2)*3**(3/4)/24 + sqrt(2)*3**(1/4)/8)}))
which is no more checkable than the previous ones...
Querying "the competition" (Mathematica) via WolframAlpha may be instructive. instructive.
My first attempts do not make me optimist...
EDIT :EDIT: A bit of numerical check leads me to think think
that the first two solutions are valid ain in a small region region
of the Argand plane around 0 :0:
sage: graphics_array([[complex_plot(Ex.subs(CSol[2*t+v]).function(u), f = lambda t, v: Ex.subs(CSol[2*t + v]).function(u)
sage: cplot = lambda t, v: complex_plot(f(t, v), (-1, 1), (-1, 1), plot_points=200) plot_points=200)
sage: graphics_array([[cplot(t, v) for v in range(2)] for t in range(2)])
Launched png viewer for Graphics Array of size 2 x 2

I have (currently) no idea of the reason of this region of validity. Someone with better knowledge of the behaviour of the (complex) rational fractions functions is welcome to explain it...
Sorry not to be more helpful.
 | 4 | No.4 Revision |
Naive approach:
sage: z, u = SR.var("z, u")
sage: Ex = 3*z^2 / (2 - 12*z^2 + sqrt(1 - 12*z^2)) - u
sage: %time Sol0 = solve(Ex, z)
CPU times: user 1.47 s, sys: 146 ms, total: 1.62 s
Wall time: 1.59 s
sage: Sol0
[z == -sqrt(1/3)*sqrt((sqrt(-12*z^2 + 1)*u + 2*u)/(4*u + 1)),
z == sqrt(1/3)*sqrt((sqrt(-12*z^2 + 1)*u + 2*u)/(4*u + 1))]
Your equation has a rational function with radicals of a polynomial in your variable of interest. Sage's default solver is unable to solve it, and returns a (set of) equation(s) equivalent to the original one (an implicit solution) :
Let's try a variant of Maxima's solver (see solve? for details):
sage: %time Sol1 = solve(Ex, z, to_poly_solve=True)
CPU times: user 2min 15s, sys: 959 ms, total: 2min 16s
Wall time: 1min 35s
sage: Sol1
[z == -sqrt(1/3)*sqrt((sqrt(-12*z^2 + 1)*u + 2*u)/(4*u + 1)),
z == sqrt(1/3)*sqrt((sqrt(-12*z^2 + 1)*u + 2*u)/(4*u + 1))]
Takes its sweet time, and returns the same (non-)solution.
Force the use of the alternate algorithm :
sage: %time Sol2 = solve(Ex, z, to_poly_solve="force")
CPU times: user 30.9 s, sys: 243 ms, total: 31.1 s
Wall time: 21.8 s
sage: Sol2
[]
SOL...
Let's get rid of the radicals, by squaring the equations until there is no radical. It can be done manually, or you can a Sympy utility for this:
sage: from sympy.solvers.solvers import unrad
sage: foo = unrad(Ex._sympy_())
sage: foo
(48*u**2*z**4 - 12*u**2*z**2 + u**2 + 24*u*z**4 - 4*u*z**2 + 3*z**4, [])
foo[0] is a (Sympy) polynomial in u and z whose roots are a superset of those of Ex (see unrad? for details).
We can try to solve it for z to get a set of candidate solutions (by squaring, we may have introduced spurious solutions...) :
sage: %time CSol = solve(foo[0]._sage_(), z); CSol
CPU times: user 15.2 ms, sys: 0 ns, total: 15.2 ms
Wall time: 15.2 ms
[z == -sqrt(2*u^2 + 1/3*sqrt(-12*u^2 + 1)*u + 2/3*u)/(4*u + 1),
z == sqrt(2*u^2 + 1/3*sqrt(-12*u^2 + 1)*u + 2/3*u)/(4*u + 1),
z == -sqrt(2*u^2 - 1/3*sqrt(-12*u^2 + 1)*u + 2/3*u)/(4*u + 1),
z == sqrt(2*u^2 - 1/3*sqrt(-12*u^2 + 1)*u + 2/3*u)/(4*u + 1)]
However, filtering the "real" solutions isn't easy: Sage is currently unable to check those candidate solutions:
sage: [Ex.subs(s).is_zero() for s in CSol]
[False, False, False, False]
This filtering may be possible by numerical checks in a "likely" region of u values. Rapid checks for u in the [-5, 5] real interval found no valid solution.
Using Sympy directly returns a set of possible implicit solutions:
sage: solve(Ex, z, algorithm="sympy")
Complement(ConditionSet(z, Eq(u/3 + z**2/(12*z**2 - sqrt(1 - 12*z**2) - 2), 0), {-sqrt(6*u**2/(48*u**2 + 24*u + 3) - u*sqrt(1 - 12*u**2)/(48*u**2 + 24*u + 3) + 2*u/(48*u**2 + 24*u + 3)), sqrt(6*u**2/(48*u**2 + 24*u + 3) - u*sqrt(1 - 12*u**2)/(48*u**2 + 24*u + 3) + 2*u/(48*u**2 + 24*u + 3)), -sqrt(6*u**2/(48*u**2 + 24*u + 3) + u*sqrt(1 - 12*u**2)/(48*u**2 + 24*u + 3) + 2*u/(48*u**2 + 24*u + 3)), sqrt(6*u**2/(48*u**2 + 24*u + 3) + u*sqrt(1 - 12*u**2)/(48*u**2 + 24*u + 3) + 2*u/(48*u**2 + 24*u + 3))}), ConditionSet(z, Eq(12*z**2 - sqrt(1 - 12*z**2) - 2, 0), {-sqrt(2)*3**(1/4)/8 - sqrt(2)*3**(3/4)/24 + I*(-sqrt(2)*3**(1/4)/8 + sqrt(2)*3**(3/4)/24), -sqrt(2)*3**(1/4)/8 - sqrt(2)*3**(3/4)/24 + I*(-sqrt(2)*3**(3/4)/24 + sqrt(2)*3**(1/4)/8), sqrt(2)*3**(3/4)/24 + sqrt(2)*3**(1/4)/8 + I*(-sqrt(2)*3**(1/4)/8 + sqrt(2)*3**(3/4)/24), sqrt(2)*3**(3/4)/24 + sqrt(2)*3**(1/4)/8 + I*(-sqrt(2)*3**(3/4)/24 + sqrt(2)*3**(1/4)/8)}))
which is no more checkable than the previous ones...
Querying "the competition" (Mathematica) via WolframAlpha may be instructive. My first attempts do not make me optimist...
EDIT: A bit of numerical check leads me to think that the first two solutions are valid in a small region of the Argand plane around 0:
sage: f = lambda t, v: Ex.subs(CSol[2*t + v]).function(u)
sage: cplot = lambda t, v: complex_plot(f(t, v), (-1, 1), (-1, 1), plot_points=200)
sage: graphics_array([[cplot(t, v) for v in range(2)] for t in range(2)])
Launched png viewer for Graphics Array of size 2 x 2

I have (currently) no idea of the reason of this region of validity. Someone with better knowledge of the behaviour of the (complex) rational functions is welcome to explain it...
EDIT 2 : For once, "the competition" fails this one :
sage: foo=mathematica("Sol=Solve[%s, %s]"%tuple(map(lambda u:repr(mathematica(u)), (Ex==u, z))))
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
Cell In [97], line 1
----> 1 foo=mathematica("Sol=Solve[%s, %s]"%tuple(map(lambda u:repr(mathematica(u)), (Ex==u, z))))
File /usr/local/sage-9/src/sage/interfaces/interface.py:298, in Interface.__call__(self, x, name)
295 pass
297 if isinstance(x, str):
--> 298 return cls(self, x, name=name)
299 try:
300 # Special methods do not and should not have an option to
301 # set the name directly, as the identifier assigned by the
302 # interface should stay consistent. An identifier with a
303 # user-assigned name might change its value, so we return a
304 # new element.
305 result = self._coerce_from_special_method(x)
File /usr/local/sage-9/src/sage/interfaces/expect.py:1496, in ExpectElement.__init__(self, parent, value, is_name, name)
1494 else:
1495 try:
-> 1496 self._name = parent._create(value, name=name)
1497 # Convert ValueError and RuntimeError to TypeError for
1498 # coercion to work properly.
1499 except (RuntimeError, ValueError) as x:
File /usr/local/sage-9/src/sage/interfaces/interface.py:516, in Interface._create(self, value, name)
514 def _create(self, value, name=None):
515 name = self._next_var_name() if name is None else name
--> 516 self.set(name, value)
517 return name
File /usr/local/sage-9/src/sage/interfaces/mathematica.py:621, in Mathematica.set(self, var, value)
619 out = self._eval_line(cmd, allow_use_file=True)
620 if len(out) > 8:
--> 621 raise TypeError("Error executing code in Mathematica\nCODE:\n\t%s\nMathematica ERROR:\n\t%s" % (cmd, out))
TypeError: Error executing code in Mathematica
CODE:
sage5=Sol=Solve[(-3*z^2)/(-2 + 12*z^2 - Sqrt[1 - 12*z^2]) == u, z];
Mathematica ERROR:
Solve::nongen: There may be values of the parameters for which some or all
solutions are not valid.
Here, Sage treats as an error what Wolfram emits as a warning. Notwithstanding :
sage: MSol=[{u[1].sage():u[2].sage() for u in v} for v in mathematica("Sol")] ; MSol
[{z: -1/3*sqrt(3)*sqrt(6*u^2/(16*u^2 + 8*u + 1) + 2*u/(16*u^2 + 8*u + 1) - sqrt(-(12*u^2 - 1)*u^2)/(16*u^2 + 8*u + 1))},
{z: 1/3*sqrt(3)*sqrt(6*u^2/(16*u^2 + 8*u + 1) + 2*u/(16*u^2 + 8*u + 1) - sqrt(-(12*u^2 - 1)*u^2)/(16*u^2 + 8*u + 1))},
{z: -sqrt(2*u^2/(16*u^2 + 8*u + 1) + 2/3*u/(16*u^2 + 8*u + 1) + 1/3*sqrt(-12*u^4 + u^2)/(16*u^2 + 8*u + 1))},
{z: sqrt(2*u^2/(16*u^2 + 8*u + 1) + 2/3*u/(16*u^2 + 8*u + 1) + 1/3*sqrt(-12*u^4 + u^2)/(16*u^2 + 8*u + 1))}]
Nice, easy... and wrong :
sage: graphics_array([[complex_plot((Ex-u).subs(z==MSol[2*u+v][z]), (-1, 1), (-1, 1)) for v in range(2)] for u in range(2)])
Launched png viewer for Graphics Array of size 2 x 2

Sorry not to be more helpful.
 | 5 | No.5 Revision |
Naive approach:
sage: z, u = SR.var("z, u")
sage: Ex = 3*z^2 / (2 - 12*z^2 + sqrt(1 - 12*z^2)) - u
sage: %time Sol0 = solve(Ex, z)
CPU times: user 1.47 s, sys: 146 ms, total: 1.62 s
Wall time: 1.59 s
sage: Sol0
[z == -sqrt(1/3)*sqrt((sqrt(-12*z^2 + 1)*u + 2*u)/(4*u + 1)),
z == sqrt(1/3)*sqrt((sqrt(-12*z^2 + 1)*u + 2*u)/(4*u + 1))]
Your equation has a rational function with radicals of a polynomial in your variable of interest. Sage's default solver is unable to solve it, and returns a (set of) equation(s) equivalent to the original one (an implicit solution) :
Let's try a variant of Maxima's solver (see solve? for details):
sage: %time Sol1 = solve(Ex, z, to_poly_solve=True)
CPU times: user 2min 15s, sys: 959 ms, total: 2min 16s
Wall time: 1min 35s
sage: Sol1
[z == -sqrt(1/3)*sqrt((sqrt(-12*z^2 + 1)*u + 2*u)/(4*u + 1)),
z == sqrt(1/3)*sqrt((sqrt(-12*z^2 + 1)*u + 2*u)/(4*u + 1))]
Takes its sweet time, and returns the same (non-)solution.
Force the use of the alternate algorithm :
sage: %time Sol2 = solve(Ex, z, to_poly_solve="force")
CPU times: user 30.9 s, sys: 243 ms, total: 31.1 s
Wall time: 21.8 s
sage: Sol2
[]
SOL...
Let's get rid of the radicals, by squaring the equations until there is no radical. It can be done manually, or you can a Sympy utility for this:
sage: from sympy.solvers.solvers import unrad
sage: foo = unrad(Ex._sympy_())
sage: foo
(48*u**2*z**4 - 12*u**2*z**2 + u**2 + 24*u*z**4 - 4*u*z**2 + 3*z**4, [])
foo[0] is a (Sympy) polynomial in u and z whose roots are a superset of those of Ex (see unrad? for details).
We can try to solve it for z to get a set of candidate solutions (by squaring, we may have introduced spurious solutions...) :
sage: %time CSol = solve(foo[0]._sage_(), z); CSol
CPU times: user 15.2 ms, sys: 0 ns, total: 15.2 ms
Wall time: 15.2 ms
[z == -sqrt(2*u^2 + 1/3*sqrt(-12*u^2 + 1)*u + 2/3*u)/(4*u + 1),
z == sqrt(2*u^2 + 1/3*sqrt(-12*u^2 + 1)*u + 2/3*u)/(4*u + 1),
z == -sqrt(2*u^2 - 1/3*sqrt(-12*u^2 + 1)*u + 2/3*u)/(4*u + 1),
z == sqrt(2*u^2 - 1/3*sqrt(-12*u^2 + 1)*u + 2/3*u)/(4*u + 1)]
However, filtering the "real" solutions isn't easy: Sage is currently unable to check those candidate solutions:
sage: [Ex.subs(s).is_zero() for s in CSol]
[False, False, False, False]
This filtering may be possible by numerical checks in a "likely" region of u values. Rapid checks for u in the [-5, 5] real interval found no valid solution.
Using Sympy directly returns a set of possible implicit solutions:
sage: solve(Ex, z, algorithm="sympy")
Complement(ConditionSet(z, Eq(u/3 + z**2/(12*z**2 - sqrt(1 - 12*z**2) - 2), 0), {-sqrt(6*u**2/(48*u**2 + 24*u + 3) - u*sqrt(1 - 12*u**2)/(48*u**2 + 24*u + 3) + 2*u/(48*u**2 + 24*u + 3)), sqrt(6*u**2/(48*u**2 + 24*u + 3) - u*sqrt(1 - 12*u**2)/(48*u**2 + 24*u + 3) + 2*u/(48*u**2 + 24*u + 3)), -sqrt(6*u**2/(48*u**2 + 24*u + 3) + u*sqrt(1 - 12*u**2)/(48*u**2 + 24*u + 3) + 2*u/(48*u**2 + 24*u + 3)), sqrt(6*u**2/(48*u**2 + 24*u + 3) + u*sqrt(1 - 12*u**2)/(48*u**2 + 24*u + 3) + 2*u/(48*u**2 + 24*u + 3))}), ConditionSet(z, Eq(12*z**2 - sqrt(1 - 12*z**2) - 2, 0), {-sqrt(2)*3**(1/4)/8 - sqrt(2)*3**(3/4)/24 + I*(-sqrt(2)*3**(1/4)/8 + sqrt(2)*3**(3/4)/24), -sqrt(2)*3**(1/4)/8 - sqrt(2)*3**(3/4)/24 + I*(-sqrt(2)*3**(3/4)/24 + sqrt(2)*3**(1/4)/8), sqrt(2)*3**(3/4)/24 + sqrt(2)*3**(1/4)/8 + I*(-sqrt(2)*3**(1/4)/8 + sqrt(2)*3**(3/4)/24), sqrt(2)*3**(3/4)/24 + sqrt(2)*3**(1/4)/8 + I*(-sqrt(2)*3**(3/4)/24 + sqrt(2)*3**(1/4)/8)}))
which is no more checkable than the previous ones...
Querying "the competition" (Mathematica) via WolframAlpha may be instructive. My first attempts do not make me optimist...
EDIT: A bit of numerical check leads me to think that the first two solutions are valid in a small region of the Argand plane around 0:
sage: f = lambda t, v: Ex.subs(CSol[2*t + v]).function(u)
sage: cplot = lambda t, v: complex_plot(f(t, v), (-1, 1), (-1, 1), plot_points=200)
sage: graphics_array([[cplot(t, v) for v in range(2)] for t in range(2)])
Launched png viewer for Graphics Array of size 2 x 2

I have (currently) no idea of the reason of this region of validity. Someone with better knowledge of the behaviour of the (complex) rational functions is welcome to explain it...
EDIT 2 : For once, "the "The competition" fails gives a formally different answer, which seems to lead to numerically similar validity regions of the roots.
Please disregard a previous version of this one :edit, which claimed to have found a failure...
sage: foo=mathematica("Sol=Solve[%s, %s]"%tuple(map(lambda u:repr(mathematica(u)), (Ex==u, (Ex==0, z))))
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
Cell In [97], [3], line 1
----> 1 foo=mathematica("Sol=Solve[%s, %s]"%tuple(map(lambda u:repr(mathematica(u)), (Ex==u, (Ex==Integer(0), z))))
File /usr/local/sage-9/src/sage/interfaces/interface.py:298, /usr/local/sage-10/src/sage/misc/lazy_import.pyx:404, in sage.misc.lazy_import.LazyImport.__call__()
402 True
403 """
--> 404 return self.get_object()(*args, **kwds)
405
406 def __repr__(self):
File /usr/local/sage-10/src/sage/interfaces/interface.py:298, in Interface.__call__(self, x, name)
295 pass
297 if isinstance(x, str):
--> 298 return cls(self, x, name=name)
299 try:
300 # Special methods do not and should not have an option to
301 # set the name directly, as the identifier assigned by the
302 # interface should stay consistent. An identifier with a
303 # user-assigned name might change its value, so we return a
304 # new element.
305 result = self._coerce_from_special_method(x)
File /usr/local/sage-9/src/sage/interfaces/expect.py:1496, /usr/local/sage-10/src/sage/interfaces/expect.py:1496, in ExpectElement.__init__(self, parent, value, is_name, name)
1494 else:
1495 try:
-> 1496 self._name = parent._create(value, name=name)
1497 # Convert ValueError and RuntimeError to TypeError for
1498 # coercion to work properly.
1499 except (RuntimeError, ValueError) as x:
File /usr/local/sage-9/src/sage/interfaces/interface.py:516, /usr/local/sage-10/src/sage/interfaces/interface.py:516, in Interface._create(self, value, name)
514 def _create(self, value, name=None):
515 name = self._next_var_name() if name is None else name
--> 516 self.set(name, value)
517 return name
File /usr/local/sage-9/src/sage/interfaces/mathematica.py:621, /usr/local/sage-10/src/sage/interfaces/mathematica.py:621, in Mathematica.set(self, var, value)
619 out = self._eval_line(cmd, allow_use_file=True)
620 if len(out) > 8:
--> 621 raise TypeError("Error executing code in Mathematica\nCODE:\n\t%s\nMathematica ERROR:\n\t%s" % (cmd, out))
TypeError: Error executing code in Mathematica
CODE:
sage5=Sol=Solve[(-3*z^2)/(-2 sage0=Sol=Solve[-u - (3*z^2)/(-2 + 12*z^2 - Sqrt[1 - 12*z^2]) == u, 0, z];
Mathematica ERROR:
Solve::nongen: There may be values of the parameters for which some or all
solutions are not valid.
Here, Sage treats wrongly interprets a Mathematica warning as an error what Wolfram emits as a , hence the workaround... The solutions warningcan. Notwithstanding be (manually) transtlated in Sage :
sage: MSol=[{u[1].sage():u[2].sage() for u in v} s} for v s in mathematica("Sol")] ; MSol
[{z: -1/3*sqrt(3)*sqrt(6*u^2/(16*u^2 + 8*u + 1) + 2*u/(16*u^2 + 8*u + 1) - sqrt(-(12*u^2 - 1)*u^2)/(16*u^2 + 8*u + 1))},
{z: 1/3*sqrt(3)*sqrt(6*u^2/(16*u^2 + 8*u + 1) + 2*u/(16*u^2 + 8*u + 1) - sqrt(-(12*u^2 - 1)*u^2)/(16*u^2 + 8*u + 1))},
{z: -sqrt(2*u^2/(16*u^2 + 8*u + 1) + 2/3*u/(16*u^2 + 8*u + 1) + 1/3*sqrt(-12*u^4 + u^2)/(16*u^2 + 8*u + 1))},
{z: sqrt(2*u^2/(16*u^2 + 8*u + 1) + 2/3*u/(16*u^2 + 8*u + 1) + 1/3*sqrt(-12*u^4 + u^2)/(16*u^2 + 8*u + 1))}]
Nice, easy... and wrong (numerically) checked :
sage: graphics_array([[complex_plot((Ex-u).subs(z==MSol[2*u+v][z]), graphics_array([[complex_plot(Ex.subs(MSol[2*u+v]), (-1, 1), (-1, 1)) 1), plot_points=200) for v in range(2)] for u in range(2)])
Launched png viewer for Graphics Array of size 2 x 2

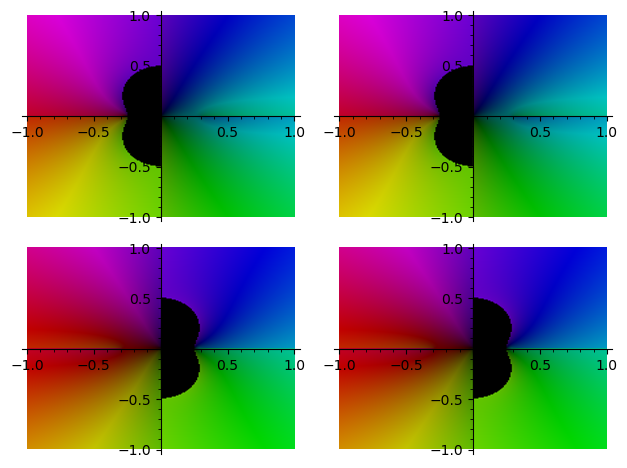
Sorry not to be more helpful.
