Revision history [back]

There are several ways to do it and you'll have to decide on which suits you best. First method: Direct use of sympy. This didn't work out the way I expected: it switched x and y after substitution:

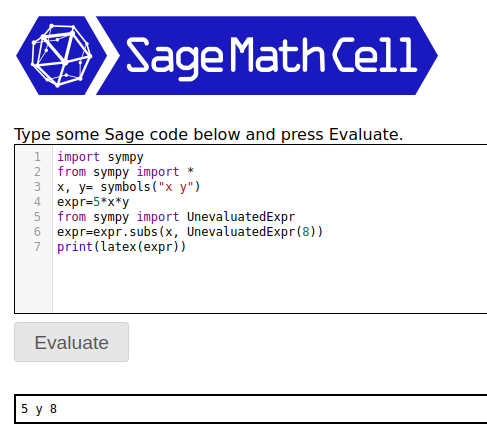
If that's okay then maybe this is good enough. I wouldn't want it swapping terms, so with a bit of fiddling came up with this, which is getting more involved:

import sympy
from sympy import *
x,y=symbols("x y")
expr = 5*x*y
from sympy import UnevaluatedExpr
print(latex(UnevaluatedExpr(sympify("5*8*y",evaluate=False))))

Now the order is correct but latex(UnevaluatedExpr(sympify("5*8*y",evaluate=False))) is a bit annoying

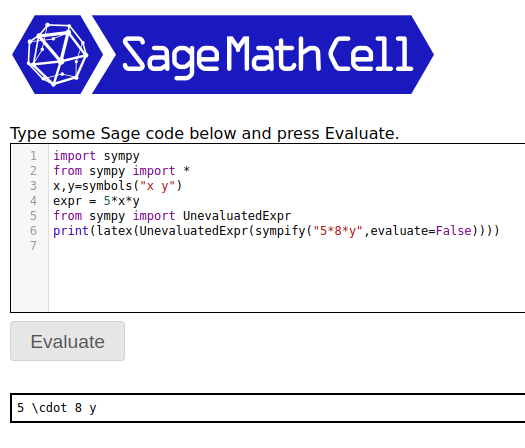
Note removing print from the last statement gives you your double escape: '5 \\cdot 8 y'

Second method is to work in strings. This will give you complete control over your output:

y=var("y")
expr = 5*x*y
expr = latex(expr).replace(r" \, ","")
s1 = expr.replace("x", r" \\cdot 8 ")
s2 = s1.replace("y",r"\\cdot 4 ")
print(s1,",  ",s2)

The output is:

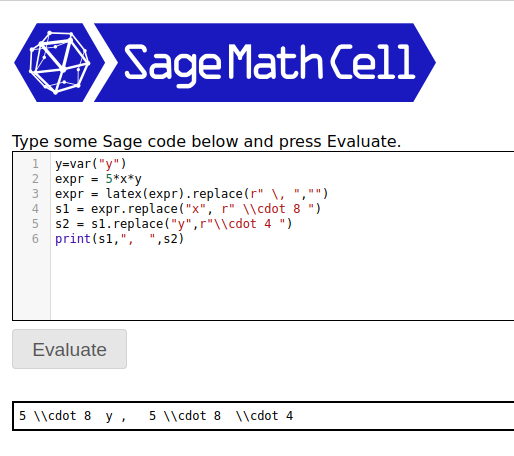
s1 is the output after the first step of substituting x for r" \cdot 8 " while s2 would be a potential second step of substituting y for r"\cdot 4 ".

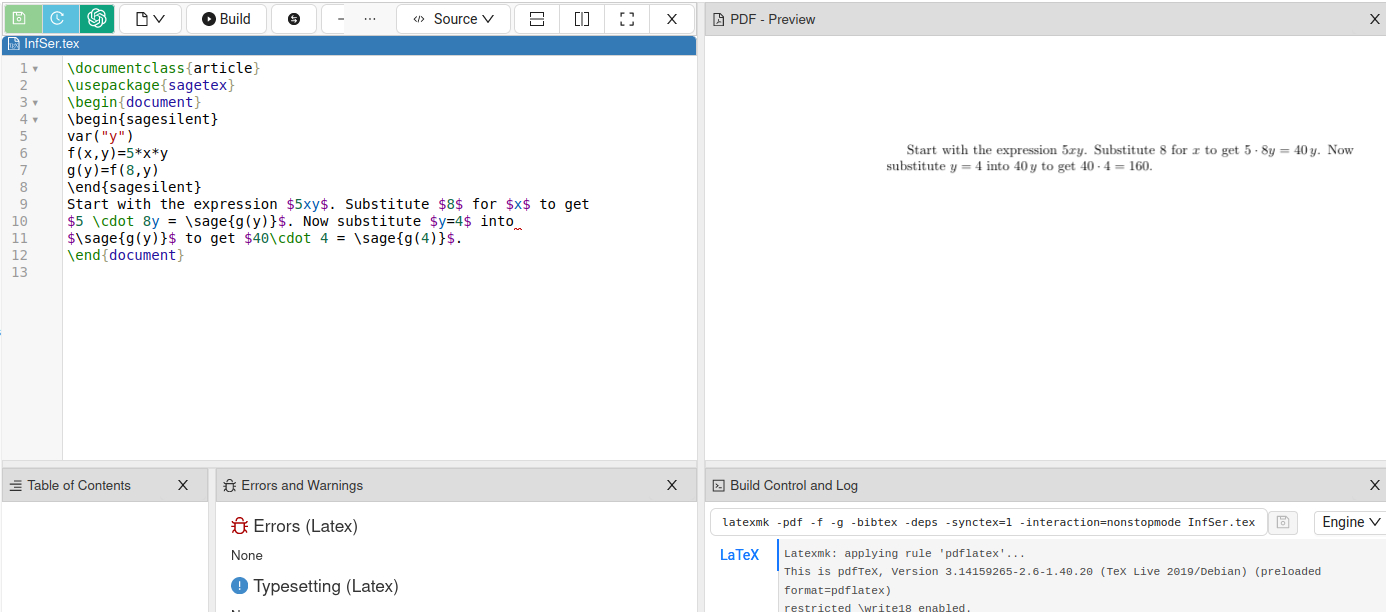
Third method, which might be useful depending on the context of how you are using the output, is to work directly in LaTeX and borrow from Sage as needed. This is typically how I work with both. Here is a sample LaTeX document:

\documentclass{article}
\usepackage{sagetex}
\begin{document}
\begin{sagesilent}
var("y")
f(x,y)=5*x*y
g(y)=f(8,y)
\end{sagesilent}
Start with the expression $5xy$. Substitute $8$ for $x$ to get
$5 \cdot 8y = \sage{g(y)}$. Now substitute $y=4$ into 
$\sage{g(y)}$ to get $40\cdot 4 = \sage{g(4)}$.
\end{document}