Ask Your Question

Revision history [back]

click to hide/show revision 1
initial version

answered 2023-01-08 22:24:28 +0200

Emmanuel Charpentier gravatar image

As in your previous question, the lhs() of your inequation $\left(\frac{x^2}{x+1}\right)$ is not a polynomial.

And the solution proposed by Sage :

sage: solve_ineq(x^2/(x+1)>=0, x)
[[x > -1]]

is correct :

  • such an inequation has meaning only for real values ;

  • $x$ being a real, $x^2$ is non-negative ; therefore, $\frac{x^2}{x+1}$ has the sign of $x+1$, which is

    • positive for $x>-1$ (except for $x=0$, where your lhs() is zero),
    • negative for $x<-1$, and
    • indeterminate for $x=-1$.

These cases exhaust the possibilities for $x\in\mathbb{R}$.

Now, $x$ can also be a non-real complex, with the constraint $\displaystyle\frac{x^2}{x+1}\in\mathbb{R}$. The latter constraint can be implemented as (x^2/(x+1)).imag()==0. Rewriting $x=a+i\,b$, we get :

sage: var("a, b", domain="real")
(a, b)
sage: solve_ineq([(x^2/(x+1)).subs(x==a+I*b).imag()==0, (x^2/(x+1)).subs(x==a+I*b)>=0], [b])
[[b == I*a, 1 != 0, 2*a == 0, 2*a + 1 != 0],
 [b == 0, a + 1 != 0, a^2 + 2*a + 1 != 0, a],
 [a + I*b + 1 > 0,
  a + I*b != 0,
  a^2 + b^2 + 2*a == 0,
  a^2 + b^2 + 2*a + 1 != 0],
 [b == 0, a + 1 > 0, a != 0, a^2 + 2*a + 1 != 0],
 [-a - I*b - 1 > 0,
  -(a + I*b)^2 > 0,
  a^2 + b^2 + 2*a == 0,
  a^2 + b^2 + 2*a + 1 != 0],
 [b == 0, -a - 1 > 0, -a^2 > 0, a^2 + 2*a + 1 != 0]]
  • The first case boils down to $x=0$ ;
  • the second to $x\neq-1$ (and misses the positivity constraint) ;
  • the third is meaningless/impossible for $a, b\in\mathbb{R}$ (except for $a=b=0$, which it excludes) ;
  • the fourth is identical to the second ;
  • the fifth leads to the same conclusions than the third ;
  • the sixth is impossible.

Sage's solve_ineq can't find the solutions (if any exists) of this form...

HTH,

As in your previous question, the lhs() of your inequation $\left(\frac{x^2}{x+1}\right)$ is not a polynomial.

And the solution proposed by Sage :

sage: solve_ineq(x^2/(x+1)>=0, x)
[[x > -1]]

is correct :

  • such an inequation has meaning only for real values ;

  • $x$ being a real, $x^2$ is non-negative ; therefore, $\frac{x^2}{x+1}$ has the sign of $x+1$, which is

    • positive for $x>-1$ (except for $x=0$, where your lhs() is zero),
    • negative for $x<-1$, and
    • indeterminate for $x=-1$.

These cases exhaust the possibilities for $x\in\mathbb{R}$.

Now, your inequation may be meaningful if $x$ can is a non-real complex alsowith the added constraint $\displaystyle\frac{x^2}{x+1}\in\mathbb{R}$ be a non-real complex, with the constraint $\displaystyle\frac{x^2}{x+1}\in\mathbb{R}$. The latter . This constraint can be implemented as (x^2/(x+1)).imag()==0. Rewriting $x=a+i\,b$, we get :

sage: var("a, b", domain="real")
(a, b)
sage: solve_ineq([(x^2/(x+1)).subs(x==a+I*b).imag()==0, (x^2/(x+1)).subs(x==a+I*b)>=0], [b])
[[b == I*a, 1 != 0, 2*a == 0, 2*a + 1 != 0],
 [b == 0, a + 1 != 0, a^2 + 2*a + 1 != 0, a],
 [a + I*b + 1 > 0,
  a + I*b != 0,
  a^2 + b^2 + 2*a == 0,
  a^2 + b^2 + 2*a + 1 != 0],
 [b == 0, a + 1 > 0, a != 0, a^2 + 2*a + 1 != 0],
 [-a - I*b - 1 > 0,
  -(a + I*b)^2 > 0,
  a^2 + b^2 + 2*a == 0,
  a^2 + b^2 + 2*a + 1 != 0],
 [b == 0, -a - 1 > 0, -a^2 > 0, a^2 + 2*a + 1 != 0]]
  • The first case boils down to $x=0$ ;
  • the second to $x\neq-1$ (and misses the positivity constraint) ;
  • the third is meaningless/impossible for $a, b\in\mathbb{R}$ (except for $a=b=0$, which it excludes) ;
  • the fourth is identical to the second ;
  • the fifth leads to the same conclusions than the third ;
  • the sixth is impossible.

Sage's solve_ineq can't find the solutions (if any exists) of this form...form. This might deserve further exploration, with more advanced techniques (think algebraic geometry...).

HTH,

As in your previous question, the lhs() of your inequation $\left(\frac{x^2}{x+1}\right)$ is not a polynomial.

And the solution proposed by Sage :

sage: solve_ineq(x^2/(x+1)>=0, x)
[[x > -1]]

is correct :

  • such an inequation has meaning only for real values ;

  • $x$ being a real, $x^2$ is non-negative ; therefore, $\frac{x^2}{x+1}$ has the sign of $x+1$, which is

    • positive for $x>-1$ (except for $x=0$, where your lhs() is zero),
    • negative for $x<-1$, and
    • indeterminate for $x=-1$.

These cases exhaust the possibilities for $x\in\mathbb{R}$.

Now, your inequation may be meaningful if $x$ is a non-real complex with the added constraint $\displaystyle\frac{x^2}{x+1}\in\mathbb{R}$. This constraint can be implemented as (x^2/(x+1)).imag()==0. Rewriting $x=a+i\,b$, we get :

sage: var("a, b", domain="real")
(a, b)
sage: solve_ineq([(x^2/(x+1)).subs(x==a+I*b).imag()==0, (x^2/(x+1)).subs(x==a+I*b)>=0], [b])
[[b == I*a, 1 != 0, 2*a == 0, 2*a + 1 != 0],
 [b == 0, a + 1 != 0, a^2 + 2*a + 1 != 0, a],
 [a + I*b + 1 > 0,
  a + I*b != 0,
  a^2 + b^2 + 2*a == 0,
  a^2 + b^2 + 2*a + 1 != 0],
 [b == 0, a + 1 > 0, a != 0, a^2 + 2*a + 1 != 0],
 [-a - I*b - 1 > 0,
  -(a + I*b)^2 > 0,
  a^2 + b^2 + 2*a == 0,
  a^2 + b^2 + 2*a + 1 != 0],
 [b == 0, -a - 1 > 0, -a^2 > 0, a^2 + 2*a + 1 != 0]]
  • The first case boils down to $x=0$ ;
  • the second to $x\neq-1$ (and misses the positivity constraint) ;
  • the third is meaningless/impossible for $a, b\in\mathbb{R}$ (except for $a=b=0$, which it excludes) ;
  • the fourth is identical to the second ;
  • the fifth leads to the same conclusions than the third ;
  • the sixth is impossible.

Sage's solve_ineq can't find the solutions (if any exists) of this form. This might deserve further exploration, with more advanced techniques (think algebraic geometry...).

EDIT : In this special case, the solution set can be computed "by hand" by rewriting $\frac{x^2}{x+1}$ as $a+i\,b$, solving $\frac{x^2}{x+1}\in\mathbb{R}$ for $b$ and substituting each of these solutions to solve $\re\left(\frac{x^2}{x+1}>=0$ :

sage: ExR=(x^2/(x+1)).subs(x==a+I*b) ; ExR
(a + I*b)^2/(a + I*b + 1)
sage: Sb=ExR.imag().factor().solve(b) ; Sb
[b == -sqrt(-a^2 - 2*a), b == sqrt(-a^2 - 2*a), b == 0]
sage: {u:solve_ineq(ExR.real().factor().subs(u)>=0, a) for u in Sb}
{b == -sqrt(-a^2 - 2*a): [[a >= 0]],
 b == sqrt(-a^2 - 2*a): [[a >= 0]],
 b == 0: [[a > -1]]}

Illustration :

sage: plot([ExR.real().factor().subs(u) for u in Sb], (a, -3, 3), ymin=-5, ymax=5, legend_label=["$%s$"%latex(u) for u in Sb], detect_poles="show")
Launched png viewer for Graphics object consisting of 5 graphics primitives

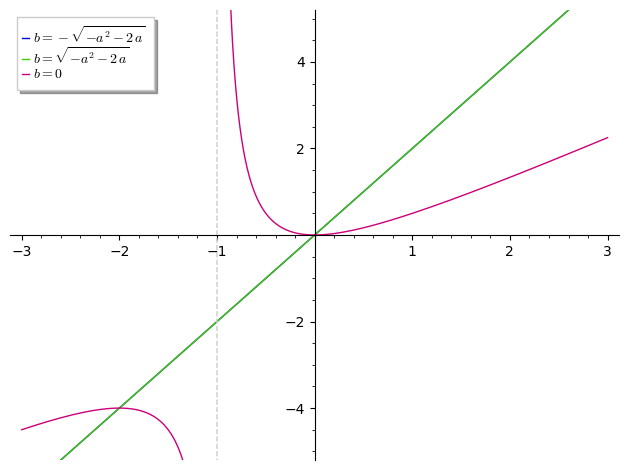
image description

HTH,

As in your previous question, the lhs() of your inequation $\left(\frac{x^2}{x+1}\right)$ is not a polynomial.

And the solution proposed by Sage :

sage: solve_ineq(x^2/(x+1)>=0, x)
[[x > -1]]

is correct :

  • such an inequation has meaning only for real values ;

  • $x$ being a real, $x^2$ is non-negative ; therefore, $\frac{x^2}{x+1}$ has the sign of $x+1$, which is

    • positive for $x>-1$ (except for $x=0$, where your lhs() is zero),
    • negative for $x<-1$, and
    • indeterminate for $x=-1$.

These cases exhaust the possibilities for $x\in\mathbb{R}$.

Now, your inequation may be meaningful if $x$ is a non-real complex with the added constraint $\displaystyle\frac{x^2}{x+1}\in\mathbb{R}$. This constraint can be implemented as (x^2/(x+1)).imag()==0. Rewriting $x=a+i\,b$, we get :

sage: var("a, b", domain="real")
(a, b)
sage: solve_ineq([(x^2/(x+1)).subs(x==a+I*b).imag()==0, (x^2/(x+1)).subs(x==a+I*b)>=0], [b])
[[b == I*a, 1 != 0, 2*a == 0, 2*a + 1 != 0],
 [b == 0, a + 1 != 0, a^2 + 2*a + 1 != 0, a],
 [a + I*b + 1 > 0,
  a + I*b != 0,
  a^2 + b^2 + 2*a == 0,
  a^2 + b^2 + 2*a + 1 != 0],
 [b == 0, a + 1 > 0, a != 0, a^2 + 2*a + 1 != 0],
 [-a - I*b - 1 > 0,
  -(a + I*b)^2 > 0,
  a^2 + b^2 + 2*a == 0,
  a^2 + b^2 + 2*a + 1 != 0],
 [b == 0, -a - 1 > 0, -a^2 > 0, a^2 + 2*a + 1 != 0]]
  • The first case boils down to $x=0$ ;
  • the second to $x\neq-1$ (and misses the positivity constraint) ;
  • the third is meaningless/impossible for $a, b\in\mathbb{R}$ (except for $a=b=0$, which it excludes) ;
  • the fourth is identical to the second ;
  • the fifth leads to the same conclusions than the third ;
  • the sixth is impossible.

Sage's solve_ineq can't find the solutions (if any exists) of this form. This might deserve further exploration, with more advanced techniques (think algebraic geometry...).

EDIT : In this special case, the solution set can be computed "by hand" by rewriting $\frac{x^2}{x+1}$ as $a+i\,b$, solving $\frac{x^2}{x+1}\in\mathbb{R}$ for $b$ (by solving $\Im\left(\frac{x^2}{x+1}\right)=0$) for $b$, and substituting each of these solutions to solve $\re\left(\frac{x^2}{x+1}>=0$ $\Re\left(\frac{x^2}{x+1}\right)>=0$ for $a$ :

sage: ExR=(x^2/(x+1)).subs(x==a+I*b) ; ExR
(a + I*b)^2/(a + I*b + 1)
sage: Sb=ExR.imag().factor().solve(b) ; Sb
[b == -sqrt(-a^2 - 2*a), b == sqrt(-a^2 - 2*a), b == 0]
sage: {u:solve_ineq(ExR.real().factor().subs(u)>=0, a) for u in Sb}
{b == -sqrt(-a^2 - 2*a): [[a >= 0]],
 b == sqrt(-a^2 - 2*a): [[a >= 0]],
 b == 0: [[a > -1]]}

Illustration :

sage: plot([ExR.real().factor().subs(u) for u in Sb], (a, -3, 3), ymin=-5, ymax=5, legend_label=["$%s$"%latex(u) for u in Sb], detect_poles="show")
Launched png viewer for Graphics object consisting of 5 graphics primitives

image description

HTH,

Copyright Sage, 2010. Some rights reserved under creative commons license. Content on this site is licensed under a Creative Commons Attribution Share Alike 3.0 license.
about | faq | help | privacy policy | terms of service
Powered by Askbot version 0.7.59