Revision history [back]

There is a subdivide_edges method but it doesn't seem to give control over the names of the new vertices.

If I understood the definition correctly then the implementation can go like this:

def total_graph(G):
    T = Graph([G.vertices() + G.edges(), G.edges() + G.line_graph().edges()])
    for (a,b,l) in G.edges():
        T.add_edge(a, (a,b,l))
        T.add_edge(b, (a,b,l))
    return T

Example 1:

sage: graphs.PathGraph(2).edges()
[(0, 1, None)]
sage: total_graph(graphs.PathGraph(2)).edges(sort=False)
[(0, 1, None), ((0, 1, None), 0, None), ((0, 1, None), 1, None)]

Example 2:

sage: graphs.PathGraph(3).edges()
[(0, 1, None), (1, 2, None)]
sage: total_graph(graphs.PathGraph(3)).edges(sort=False)
[((0, 1, None), (1, 2, None), None), (0, 1, None), ((0, 1, None), 0, None), (1, 2, None), ((0, 1, None), 1, None), ((1, 2, None), 1, None), ((1, 2, None), 2, None)]
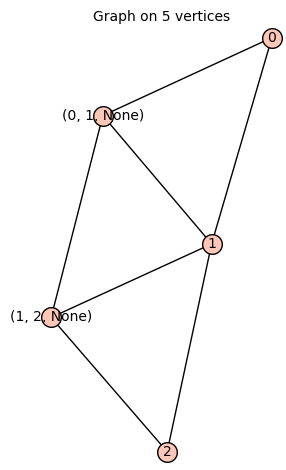
sage: total_graph(graphs.PathGraph(3))

total graph of path graph

There is a subdivide_edges method but it doesn't seem to give control over the names of the new vertices.

If I understood the definition correctly then the implementation can go like this:

def total_graph(G):
    T = Graph([G.vertices() + G.edges(), G.edges() + G.line_graph().edges()])
G.union(G.line_graph())
    for (a,b,l) in G.edges():
        T.add_edge(a, (a,b,l))
        T.add_edge(b, (a,b,l))
    return T

Example 1:

sage: graphs.PathGraph(2).edges()
[(0, 1, None)]
sage: total_graph(graphs.PathGraph(2)).edges(sort=False)
[(0, 1, None), ((0, 1, None), 0, None), ((0, 1, None), 1, None)]

Example 2:

sage: graphs.PathGraph(3).edges()
[(0, 1, None), (1, 2, None)]
sage: total_graph(graphs.PathGraph(3)).edges(sort=False)
[((0, 1, None), (1, 2, None), None), (0, 1, None), ((0, 1, None), 0, None), (1, 2, None), ((0, 1, None), 1, None), ((1, 2, None), 1, None), ((1, 2, None), 2, None)]
sage: total_graph(graphs.PathGraph(3))

total graph of path graph