Revision history [back]
 | 1 | initial version |
The syntax f(x) = x^2 defines a callable symbolic expression f. Callable symbolic expressions are limited in the type of arguments they can take; in particular they cannot take functions as arguments.
But you can define an ordinary Python function instead:
def error(function1, function2, xmin, xmax):
x = var('x')
return N(integrate(abs(function1(x)-function2(x)),x,xmin,xmax))
and then:
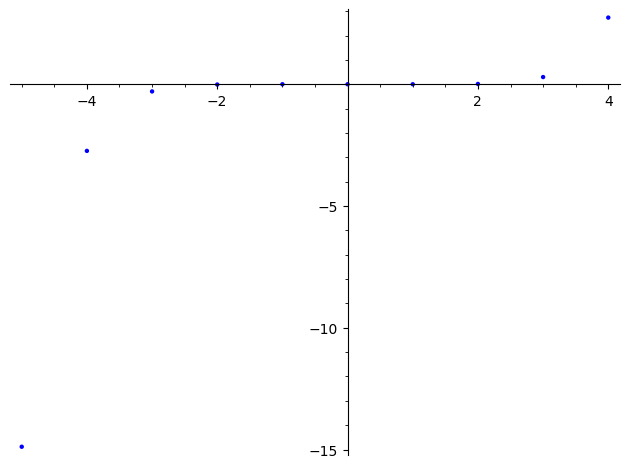
sage: nsin(x)=x-x^3/factorial(3)+x^5/factorial(5)
sage: point2d((k, error(nsin,sin,-k,k)) for k in range(-5, 5))
In the error function I defined the local variable x to be the symbolic variable named x, to avoid relying on the assumption that the variable x has already been defined that way elsewhere. It is defined that way by default in a fresh SageMath session, but it's not uncommon to re-define x, and we should allow that without breaking our function.
 | 2 | No.2 Revision |
The syntax f(x) = x^2 defines a callable symbolic expression f. Callable symbolic expressions are limited in the type of arguments they can take; in particular they cannot take functions as arguments.
But you can define an ordinary Python function instead:
def error(function1, function2, xmin, xmax):
x = var('x')
return N(integrate(abs(function1(x)-function2(x)),x,xmin,xmax))
and then:
sage: nsin(x)=x-x^3/factorial(3)+x^5/factorial(5)
sage: point2d((k, error(nsin,sin,-k,k)) for k in range(-5, 5))

In the error function I defined the local variable x to be the symbolic variable named x, to avoid relying on the assumption that the variable x has already been defined that way elsewhere. It is defined that way by default in a fresh SageMath session, but it's not uncommon to re-define x, and we should allow that without breaking our function.
x as a (third) parameter in the error function instead. 
