Revision history [back]

Note that ?Posets gives the following information on the functionality of this constructor, among other lines:

  The enumerated set of all posets on 3 elements, up to an
   isomorphism:

      sage: Posets(3)
      Posets containing 3 elements

The accent is put on up to isomorphism. For instance, we may miss the following poset from the list:

sage: pp = Poset(([0..5], [[0,2],[2,4],[3,5],[1,3]]))
sage: pp.show()

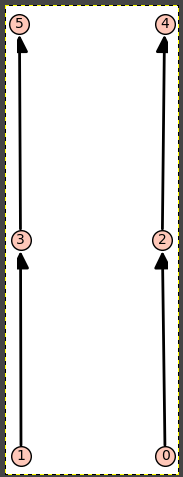
Well, this poset is not exactly in this shape in P, instead we have:

sage: p0, = [p for p in P if p.is_isomorphic(pp)]
sage: p0.relations()
[[3, 3],
 [3, 4],
 [3, 5],
 [4, 4],
 [4, 5],
 [5, 5],
 [0, 0],
 [0, 1],
 [0, 2],
 [1, 1],
 [1, 2],
 [2, 2]]
sage: p0.minimal_elements()
[3, 0]
sage: pp.minimal_elements()
[1, 0]

(P has only $318$ elements, we would have more than $6!$ if the totally ordered posets would have been individually in there, instead as one representative for this isomorphism class.)

Some possibility to restrict to "interesting posets" (that may match or not the purpose) is as follows:

sage: A0 = [p for p in P if max([len(chain) for chain in p.chains()]) == 3 and len(p.minimal_elements()) == 2 and len(p.maximal_elements()) == 2]
sage: len(A0)
35

and now write some code that searches for two disjoint chains of maximal length $3$ in each $p\in A_0$...