Revision history [back]
 | 1 | initial version |
Hello, @F. Semih Dündar! I can see a couple of problems with your code. First of all, there is no need to define $q$ and $qdot$ as formal functions, since that is implicitly assumed. Second, you only need to pass the RHS (right hand side) of the differential equations. Finally, the ics parameter must be of the form [t0, q0, qdot0].
With those considerations, your code should look like this:
var('t, qdot, q') # independent variable and functions
# Equations of motion
eom1 = qdot
eom2 = -(qdot(t))^2 - q(t)
# Initial conditions
q0 = 0
qdot0 = 1
sol = desolve_system_rk4([eom1, eom2], ivar=t, vars=[q, qdot], ics = [0, q0, qdot0], end_points=1.8, step=0.01)
S = [(t, q) for t, q, qdot in sol]
list_plot(S, plotjoined=True)
I think a few additional clarifications are in order. As mentioned, you only need the RHS of the DEs; that is why I removed part of $oem1$ and $oem2$ (specifically, the LHS and the ==). The vars parameter implicitly indicate that your system is of the form
$$q' = oem1$$ $$qdot' = oem2$$
so this code defines the same system you intended.
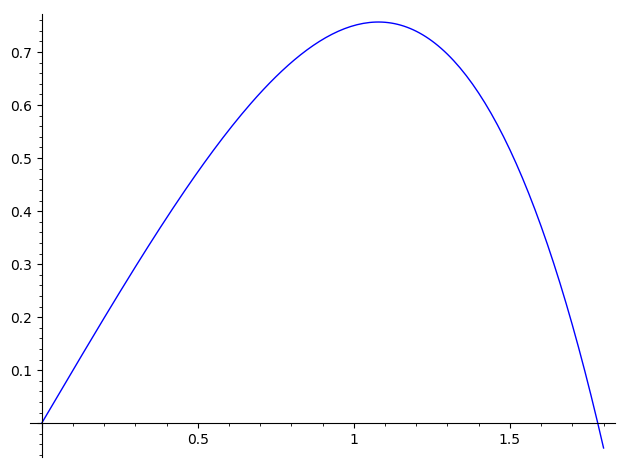
I have used the end_points=1.8 parameter in order to solve in the interval $[0, 1.8]$---after $t\approx1.8$, the value of $q$ is negative, which I assumed not to be desirable, although I don't know the context in which you are trying to solve this (so maybe you would like to modify that parameter if needed).
On the other hand, when I plotted the solution, due to the small domain, I obtained a pointy curve, so I used the step=0.01 parameter, in order to decrease the step length, and obtain a more refined solution.
The last two lines are intended to obtain a plot of $q$ alone, without including $qdot$. (I assume they are clear to you, but feel free to ask otherwise.)
Here is the resulting image:
 | 2 | No.2 Revision |
Hello, @F. Semih Dündar! I can see a couple of problems with your code. First of all, there is no need to define $q$ and $qdot$ as formal functions, since that is implicitly assumed. Second, you only need to pass the RHS (right hand side) of the differential equations. Finally, the ics parameter must be of the form [t0, q0, qdot0].
With those considerations, your code should look like this:
var('t, qdot, q') # independent variable and functions
# Equations of motion
eom1 = qdot
eom2 = -(qdot(t))^2 - q(t)
# Initial conditions
q0 = 0
qdot0 = 1
sol = desolve_system_rk4([eom1, eom2], ivar=t, vars=[q, qdot], ics = [0, q0, qdot0], end_points=1.8, step=0.01)
S = [(t, q) for t, q, qdot in sol]
list_plot(S, plotjoined=True)
I think a few additional clarifications are in order. As mentioned, you only need the RHS of the DEs; that is why I removed part of $oem1$ and $oem2$ (specifically, the LHS and the ==). The vars parameter implicitly indicate that your system is of the form
$$q' = oem1$$ $$qdot' = oem2$$
so this code defines the same system you intended.
I have used the end_points=1.8 parameter in order to solve in the interval $[0, 1.8]$---after $t\approx1.8$, the value of $q$ is negative, which I assumed not to be desirable, although I don't know the context in which you are trying to solve this (so maybe you would like to modify that parameter if needed).
On the other hand, when I plotted the solution, due to the small domain, I obtained a pointy curve, so I used the step=0.01 parameter, in order to decrease the step length, and obtain a more refined solution.
The last two lines are intended to obtain a plot of $q$ alone, without including $qdot$. (I assume they are clear to you, but feel free to ask otherwise.)
Here is the resulting image:

I hope this helps!
