Revision history [back]

One solution is to use Knuth's dancing links algorithm which is implemented in Sage. Assuming the vertices of the graph are integers in the range(number_of_vertices), the method below will work:

from sage.combinat.matrices.dancing_links import dlx_solver
def find_matching(G):
    rows = [[a,b] for (a,b,_) in G.edges()]
    dlx = dlx_solver(rows)
    solution = dlx.one_solution(ncpus=1)
    if solution:
        return [rows[a] for a in solution]
    else:
        return None

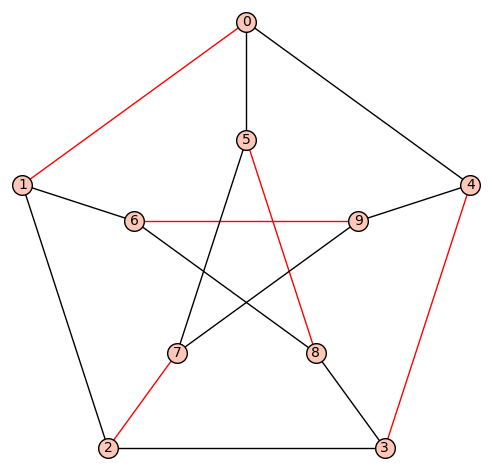
Then, on the Petersen graph, it gives:

sage: G = graphs.PetersenGraph()
sage: matching = find_matching(G)
[[2, 7], [0, 1], [5, 8], [3, 4], [6, 9]]
sage: G.plot(edge_colors={'red':matching})

Another solution is to reduce the problem to SAT and use Sage SAT solvers or you may also review the ticket I wrote recently about the reduction of dancing links instance to SAT instance.

One solution is to use Knuth's dancing links algorithm which is implemented in Sage. Assuming the vertices of the graph are integers in the range(number_of_vertices), the method below will work:

from sage.combinat.matrices.dancing_links import dlx_solver
def find_matching(G):
    rows = [[a,b] for (a,b,_) in G.edges()]
    dlx = dlx_solver(rows)
    solution = dlx.one_solution(ncpus=1)
    if solution:
        return [rows[a] for a in solution]
    else:
        return None

Then, on the Petersen graph, it gives:

sage: G = graphs.PetersenGraph()
sage: matching = find_matching(G)
sage: matching
[[2, 7], [0, 1], [5, 8], [3, 4], [6, 9]]
sage: G.plot(edge_colors={'red':matching})

Another solution is to reduce the problem to SAT and use Sage SAT solvers or you may also review the ticket I wrote recently about the reduction of dancing links instance to SAT instance.