Revision history [back]

I'm unaware of anything built in to find the strong matching number. However, it's easy enough to put some code together. Sage is able to look for subraphs with subgraph_search. You can insist that the subgraph is induced as well. The Petersen graph has ten vertices so a strong matching could be at most 5. The for loop has i run from 1 to 5, the forbidden subgraphs are set to i*graphs.CompleteGraph(2) and then Sage looks for that subgraph.

P = graphs.PetersenGraph()
for i in range(1,6):
    forbidden_subgraphs = [i*graphs.CompleteGraph(2)]
    for H in forbidden_subgraphs:
        if P.subgraph_search(H,induced=True):
            print i, "Yes"
        else:
            print i, "No"

The result in a Sage Notebook is shown below. It indicates Sage found an induced matching on 1 edge, 2 edges, and 3 edges. It could not find one on 4 edges so, of course, it can't find one on five edges. This would mean the strong matching number of the Petersen graph is 3.

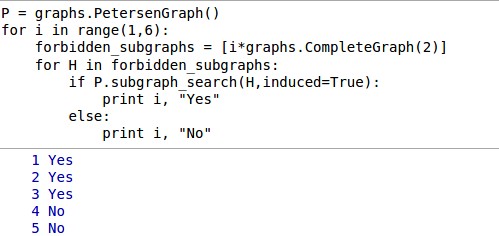
I'm unaware of anything built in to find the strong matching number. However, it's easy enough to put some code together. Sage is able to look for subraphs with subgraph_search. You can insist that the subgraph is induced as well. The Petersen graph has ten vertices so a the strong matching number could be at most 5. The for loop has i run from 1 to 5, the forbidden subgraphs are set to i*graphs.CompleteGraph(2) and then Sage looks for that subgraph.

P = graphs.PetersenGraph()
for i in range(1,6):
    forbidden_subgraphs = [i*graphs.CompleteGraph(2)]
    for H in forbidden_subgraphs:
        if P.subgraph_search(H,induced=True):
            print i, "Yes"
        else:
            print i, "No"

The result in a Sage Notebook is shown below. It indicates Sage found an induced matching on 1 edge, 2 edges, and 3 edges. It could not find one on 4 edges so, of course, it can't find one on five edges. This would mean the strong matching number of the Petersen graph is 3.

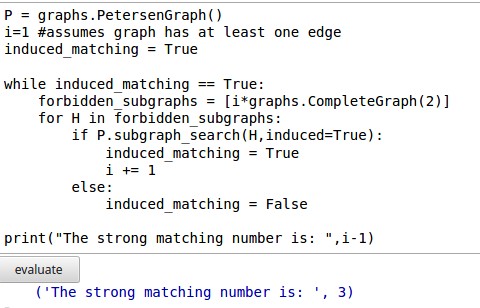
I'm unaware of anything built in to find the strong matching number. However, it's easy enough to put some code together. Sage is able to look for subraphs with subgraph_search. You can insist that the subgraph is induced as well. The Petersen graph has ten vertices so the strong matching number could be at most 5. The for loop has i run from 1 to 5, the forbidden subgraphs are set to i*graphs.CompleteGraph(2) and then Sage looks for that subgraph.

P = graphs.PetersenGraph()
for i in range(1,6):
i=1 #assumes graph has at least one edge
induced_matching = True

while induced_matching == True:
    forbidden_subgraphs = [i*graphs.CompleteGraph(2)]
    for H in forbidden_subgraphs:
        if P.subgraph_search(H,induced=True):
            print i, "Yes"
induced_matching = True
            i += 1
        else:
            print i, "No"
induced_matching = False

print("The strong matching number is: ",i-1)

The result in a Sage Notebook is shown below. It indicates Sage found an induced matching on 1 edge, 2 edges, and 3 edges. It could not find one on 4 edges so, of course, it can't find one on five edges. This would mean the strong matching number of the Petersen graph is 3.below.