Revision history - ASKSAGE: Sage Q&A Forum

Here is a function constructing the group

def my_congruence_group(B, N):
    M = MatrixSpace(Zmod(N), 2)
    B = M(B)
    assert (B**2).is_zero()
    G = SL(2,Zmod(N))
    I = G.one()
    Gsage = SL(2, Zmod(N))
    Hsage = Gsage.subgroup([I + k*B for k in range(N)])
    G = libgap(Gsage)
    H = libgap(Hsage)
    C = libgap.RightCosets(G,H)
    L = libgap(Gsage([1,1,0,1]))
    R = libgap(Gsage([1,0,1,1]))
    S2 = libgap(Gsage([0,-1,1,0]))
    S3 = libgap(Gsage([0,1,-1,1]))
    l = libgap.Permutation(L, C, libgap.OnRight)
    r = libgap.Permutation(R, C, libgap.OnRight)
    s2 = libgap.Permutation(S2, C, libgap.OnRight)
    s3 = libgap.Permutation(S3, C, libgap.OnRight)
    S = SymmetricGroup(C.Size().sage())
    lsage = S(l)
    rsage = S(r)
    s2sage = S(s2)
    s3sage = S(s3)    
    return ArithmeticSubgroup_Permutation(L=lsage, R=rsage, S2=s2sage, S3=s3sage)

You can just copy paste the code and use it as

sage: N = 6
sage: B = [2,1,2,4]
sage: G = my_congruence_group(B, N)
sage: G.gens()   # some generators for the group
(
[1 3]  [ 3 -2]  [ 11 -25]
[0 1], [ 2 -1], [  4  -9]
)
sage: print(G.genus())  # the genus of the quotient
0
sage: print(G.nu2(), G.nu3(), G.ncusps())  # elliptic points and cusps on the quotient
0 0 4
sage: F = G.farey_symbol()
sage: F.fundamental_domain()   # plot a fundamental domain

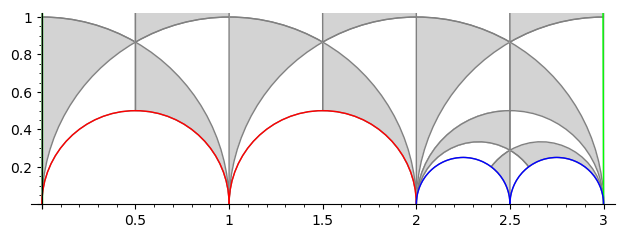
image description

You should have a look atSageMath documentation on subgroups of SL(2,Z) documentation to learn how to use G. in particular the section "Arithmetic subgroups defined by permutations of cosets" which is how I build your group and "Farey Symbol for arithmetic subgroups of PSL2(Z)" which teach you how constructing the fundamental domain works

Here is a function constructing the group

def my_congruence_group(B, N):
    M = MatrixSpace(Zmod(N), 2)
    B = M(B)
    assert (B**2).is_zero()
    G = SL(2,Zmod(N))
    I = G.one()
    Gsage = SL(2, Zmod(N))
    Hsage = Gsage.subgroup([I + k*B for k in range(N)])
    G = libgap(Gsage)
    H = libgap(Hsage)
    C = libgap.RightCosets(G,H)
    L = libgap(Gsage([1,1,0,1]))
    R = libgap(Gsage([1,0,1,1]))
    S2 = libgap(Gsage([0,-1,1,0]))
    S3 = libgap(Gsage([0,1,-1,1]))
    l = libgap.Permutation(L, C, libgap.OnRight)
    r = libgap.Permutation(R, C, libgap.OnRight)
    s2 = libgap.Permutation(S2, C, libgap.OnRight)
    s3 = libgap.Permutation(S3, C, libgap.OnRight)
    S = SymmetricGroup(C.Size().sage())
    lsage = S(l)
    rsage = S(r)
    s2sage = S(s2)
    s3sage = S(s3)    
    return ArithmeticSubgroup_Permutation(L=lsage, R=rsage, S2=s2sage, S3=s3sage)

You can just copy paste the code and use it as

sage: N = 6
sage: B = [2,1,2,4]
sage: G = my_congruence_group(B, N)
sage: G.gens()   # some generators for the group
(
[1 3]  [ 3 -2]  [ 11 -25]
[0 1], [ 2 -1], [  4  -9]
)
sage: print(G.genus())  # the genus of the quotient
0
sage: print(G.nu2(), G.nu3(), G.ncusps())  # elliptic points and cusps on the quotient
0 0 4
sage: F = G.farey_symbol()
sage: F.fundamental_domain()   # plot a fundamental domain

image description

You should have a look atSageMath documentation on subgroups of SL(2,Z) documentation to learn how to use G. in particular the section "Arithmetic subgroups defined by permutations of cosets" which is how I build your group and "Farey Symbol for arithmetic subgroups of PSL2(Z)" which teach you how constructing the fundamental domain works

EDIT: Though I suspect that all your groups are just conjugate to $\Gamma_1(N)$ or $\Gamma_0(N)$ (or at least close enough). The only matrix $B$ with $B^2= 0$ are conjugate to $\begin{pmatrix}0&b\\0&0\end{pmatrix}$.

Here is a function constructing the group

def my_congruence_group(B, N):
    M = MatrixSpace(Zmod(N), 2)
    B = M(B)
    assert (B**2).is_zero()
     G = SL(2,Zmod(N))
    I = G.one()
    Gsage = SL(2, Zmod(N))
    Hsage = Gsage.subgroup([I L = G([1,1,0,1])
    R = G([1,0,1,1])
    S2 = G([0,-1,1,0])
    S3 = G([0,1,-1,1])

    H = G.subgroup([1 + k*B for k in range(N)])
    G = libgap(Gsage)
    H = libgap(Hsage)
    C = libgap.RightCosets(G,H)
    L = libgap(Gsage([1,1,0,1]))
    R = libgap(Gsage([1,0,1,1]))
    S2 = libgap(Gsage([0,-1,1,0]))
    S3 = libgap(Gsage([0,1,-1,1]))
    l = libgap.Permutation(L, C, libgap.OnRight)
    r = libgap.Permutation(R, C, libgap.OnRight)
    s2 = libgap.Permutation(S2, C, libgap.OnRight)
    s3 = libgap.Permutation(S3, C, libgap.OnRight)
    S = SymmetricGroup(C.Size().sage())
    lsage = S(l)
    rsage = S(r)
    s2sage = S(s2)
    s3sage = S(s3)    
    return ArithmeticSubgroup_Permutation(L=lsage, R=rsage, S2=s2sage, S3=s3sage)
ArithmeticSubgroup_Permutation(L=l.sage(), R=r.sage(), S2=s2.sage(), S3=s3.sage())

You can just copy paste the code and use it as

sage: N = 6
sage: B = [2,1,2,4]
sage: G = my_congruence_group(B, N)
sage: G.gens()   # some generators for the group
(
[1 3]  [ 3 -2]  [ 11 -25]
[0 1], [ 2 -1], [  4  -9]
)
sage: print(G.genus())  # the genus of the quotient
0
sage: print(G.nu2(), G.nu3(), G.ncusps())  # elliptic points and cusps on the quotient
0 0 4
sage: F = G.farey_symbol()
sage: F.fundamental_domain()   # plot a fundamental domain

image description

You should have a look atSageMath documentation on subgroups of SL(2,Z) documentation to learn how to use G. in particular the section "Arithmetic subgroups defined by permutations of cosets" which is how I build your group and "Farey Symbol for arithmetic subgroups of PSL2(Z)" which teach you how constructing the fundamental domain works

EDIT: Though I suspect that all your groups are just conjugate to $\Gamma_1(N)$ or $\Gamma_0(N)$ (or at least close enough). The only matrix $B$ with $B^2= 0$ are conjugate to $\begin{pmatrix}0&b\\0&0\end{pmatrix}$.

Here is a function constructing the group

def my_congruence_group(B, N):
    M = MatrixSpace(Zmod(N), 2)
    B = M(B)
    assert (B**2).is_zero()
     G = SL(2, Zmod(N))
    L = G([1,1,0,1])
    R = G([1,0,1,1])
    S2 = G([0,-1,1,0])
    S3 = G([0,1,-1,1])

    H = G.subgroup([1 + k*B for k in range(N)])
    C = libgap.RightCosets(G,H)
libgap.RightCosets(G, H)

    l = libgap.Permutation(L, libgap.Permutation(G([1,1,0,1]), C, libgap.OnRight)
    r = libgap.Permutation(R, libgap.Permutation(G([1,0,1,1]), C, libgap.OnRight)
    s2 = libgap.Permutation(S2, libgap.Permutation(G([0,-1,1,0]), C, libgap.OnRight)
    s3 = libgap.Permutation(S3, libgap.Permutation(G([0,1,-1,1]), C, libgap.OnRight)

    return ArithmeticSubgroup_Permutation(L=l.sage(), R=r.sage(), S2=s2.sage(), S3=s3.sage())

You can just copy paste the code and use it as

sage: N = 6
sage: B = [2,1,2,4]
sage: G = my_congruence_group(B, N)
sage: G.gens()   # some generators for the group
(
[1 3]  [ 3 -2]  [ 11 -25]
[0 1], [ 2 -1], [  4  -9]
)
sage: print(G.genus())  # the genus of the quotient
0
sage: print(G.nu2(), G.nu3(), G.ncusps())  # elliptic points and cusps on the quotient
0 0 4
sage: F = G.farey_symbol()
sage: F.fundamental_domain()   # plot a fundamental domain

image description

You should have a look atSageMath documentation on subgroups of SL(2,Z) documentation to learn how to use G. in particular the section "Arithmetic subgroups defined by permutations of cosets" which is how I build your group and "Farey Symbol for arithmetic subgroups of PSL2(Z)" which teach you how constructing the fundamental domain works

EDIT: Though I suspect that all your groups are just conjugate to $\Gamma_1(N)$ or $\Gamma_0(N)$ (or at least close enough). The only matrix $B$ with $B^2= 0$ are conjugate to $\begin{pmatrix}0&b\\0&0\end{pmatrix}$.

Revision history [back]