Revision history [back]

Let me manually make the substitution $|x+iy|^2 = x^2 + y^2$ (it seems not easy to do in SageMath):

ineqn = (x+2)^2 + y^2 > x^2 + (y-2)^2 + 1

Then you can plot immediately:

sage: region_plot(ineqn, (-10,10), (-10,10))

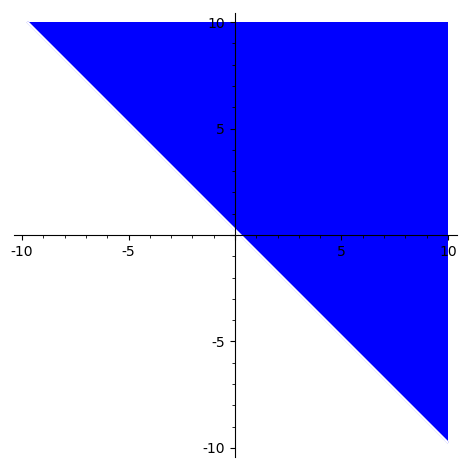
You can also solve algebraically, using a slight workaround:

sage: ineqn.operator()((ineqn.lhs() - ineqn.rhs()).full_simplify(), 0)
4*x + 4*y - 1 > 0

Indeed, replacing ineqn by 4*y + 4*x - 1 > 0 produces the same picture.

You can also use the interface to QEPCAD to make a "cylindrical algebraic decomposition":

sage: qepcad((x+2)^2+y^2>x^2+(y-2)^2+1)
4 y + 4 x - 1 > 0

The output is a string, in QEPCAD syntax, which you can translate into SageMath by hand.

Let me manually make the substitution $|x+iy|^2 = x^2 + y^2$ (it seems not easy to do in SageMath):

var('x,y')
ineqn = (x+2)^2 + y^2 > x^2 + (y-2)^2 + 1

Then you can plot immediately:

sage: region_plot(ineqn, (-10,10), (-10,10))

You can also solve algebraically, using a slight workaround:

sage: ineqn.operator()((ineqn.lhs() - ineqn.rhs()).full_simplify(), 0)
4*x + 4*y - 1 > 0

Indeed, replacing ineqn by 4*x + 4*y + 4*x - 1 > 0 produces the same picture.

You can also use the interface to QEPCAD to make a "cylindrical algebraic decomposition":

sage: qepcad((x+2)^2+y^2>x^2+(y-2)^2+1)
qepcad(ineqn)
4 y + 4 x - 1 > 0

The output is a string, in QEPCAD syntax, which you can translate into SageMath by hand.