Revision history [back]

I'm a little confused by your question. First, you haven't created a SageTeX example. A SageTeX example is a LaTeX file that relies on the SageTeX package to create output. Second, your output gives LaTeX output but not for your code since your denominator is 16 and not 420. Here is a SageTeX example for your problem

\documentclass{article}
\usepackage{sagetex}
\begin{document}
\begin{sagesilent}
x = 16       # Denominator
MyRange = 16
output = r""
for n in range (1,MyRange):
    if  n<MyRange-1:
        if gcd(n,x)==1:
            output += r"\frac{%s}{%s}, "%(n,x)
        else:
            output += r"\frac{%s}{%s}=\frac{%s}{%s}, "%(n,x,numerator(n/x),denominator(n/x))
    else:
      output += r"\frac{%s}{%s}"%(n,x)
\end{sagesilent}
\noindent $\sagestr{output}$
\end{document}

When run using LaTeX this gives the picture below

The approach I used was to see if the numerator and denominator were coprime, if gcd(n,x)==1, in which case output the fraction as is, otherwise typeset fraction and then what it simplifies to, using numerator() and denominator. Finally, to account for the commas and final fraction with no comma after it, I used the code if n<myrange-1 as="" my="" guide="" when="" to="" add="" a="" comma.="" the="" last="" term,="" when="" n="MyRange-1" will="" not="" be="" followed="" by="" any="" punctuation.="" <="" p="">

I'm a little confused by your question. First, you haven't created a SageTeX example. A SageTeX example is a LaTeX file that relies on the SageTeX package to create output. Second, your output gives LaTeX output but not for your code since your denominator is 16 and not 420. Here is a SageTeX example for your problem

\documentclass{article}
\usepackage{sagetex}
\begin{document}
\begin{sagesilent}
x = 16       # Denominator
MyRange = 16
output = r""
for n in range (1,MyRange):
    if  n<MyRange-1:
        if gcd(n,x)==1:
            output += r"\frac{%s}{%s}, "%(n,x)
        else:
            output += r"\frac{%s}{%s}=\frac{%s}{%s}, "%(n,x,numerator(n/x),denominator(n/x))
    else:
      output += r"\frac{%s}{%s}"%(n,x)
\end{sagesilent}
\noindent $\sagestr{output}$
\end{document}

When run using LaTeX this gives the picture below

The approach I used was to see if the numerator and denominator were coprime, if gcd(n,x)==1, in which case output the fraction as is, otherwise typeset fraction and then what it simplifies to, using numerator() and denominator. Finally, to account for the commas and final fraction with no comma after it, I used the code if n<myrange-1 "if n<myrange-1" as="" my="" guide="" when="" to="" add="" a="" comma.="" the="" last="" term,="" when="" n="MyRange-1" "n="MyRange-1"" will="" not="" be="" followed="" by="" any="" punctuation.="" <="" punctuation.<="" p="">

I'm a little confused by your question. First, you haven't created a SageTeX example. A SageTeX example is a LaTeX file that relies on the SageTeX package to create output. Second, your output gives LaTeX output but not for your code since your denominator is 16 and not 420. Here is a SageTeX example for your problem

\documentclass{article}
\usepackage{sagetex}
\begin{document}
\begin{sagesilent}
x = 16       # Denominator
MyRange = 16
output = r""
for n in range (1,MyRange):
    if  n<MyRange-1:
        if gcd(n,x)==1:
            output += r"\frac{%s}{%s}, "%(n,x)
        else:
            output += r"\frac{%s}{%s}=\frac{%s}{%s}, "%(n,x,numerator(n/x),denominator(n/x))
    else:
      output += r"\frac{%s}{%s}"%(n,x)
\end{sagesilent}
\noindent $\sagestr{output}$
\end{document}

When run using LaTeX this gives the picture below

The approach I used was to see if the numerator and denominator were coprime, if gcd(n,x)==1, in which case output the fraction as is, otherwise typeset fraction and then what it simplifies to, using numerator() and denominator. Finally, to account for the commas and final fraction with no comma after it, I used the code "if n<myrange-1" as="" my="" guide="" when="" to="" add="" a="" comma.="" the="" last="" term,="" when="" "n="MyRange-1"" will="" not="" be="" followed="" by="" any="" punctuation.<="" p="">

I'm a little confused by your question. First, you haven't created a SageTeX example. A SageTeX example is a LaTeX file that relies on the SageTeX package to create output. Second, your output gives LaTeX output but not for your code since your denominator is 16 and not 420. Here is a SageTeX example for your problem

\documentclass{article}
\usepackage{sagetex}
\begin{document}
\begin{sagesilent}
x = 16       # Denominator
MyRange = 16
output = r""
for n in range (1,MyRange):
    if  n<MyRange-1:
        if gcd(n,x)==1:
            output += r"\frac{%s}{%s}, "%(n,x)
        else:
            output += r"\frac{%s}{%s}=\frac{%s}{%s}, "%(n,x,numerator(n/x),denominator(n/x))
    else:
      output += r"\frac{%s}{%s}"%(n,x)
\end{sagesilent}
\noindent $\sagestr{output}$
\end{document}

When run using LaTeX this gives the picture below

The approach I used was to see if the numerator and denominator were coprime, if gcd(n,x)==1, in which case output the fraction as is, otherwise typeset fraction and then what it simplifies to, using numerator() and denominator. Finally, to account for the commas and final fraction with no comma after it, I printed out commas until the last term, which I assume was 1 less than MyRange.

I'm a little confused by your question. First, you haven't created a SageTeX example. A SageTeX example is a LaTeX file that relies on the SageTeX package to create output. Second, your output gives LaTeX output but not for your code since your denominator is 16 and not 420. Here is a SageTeX example for your problem

\documentclass{article}
\usepackage{sagetex}
\begin{document}
\begin{sagesilent}
x = 16       # Denominator
MyRange = 16
output = r""
for n in range (1,MyRange):
    if  n<MyRange-1:
        if gcd(n,x)==1:
            output += r"\frac{%s}{%s}, "%(n,x)
        else:
            output += r"\frac{%s}{%s}=\frac{%s}{%s}, "%(n,x,numerator(n/x),denominator(n/x))
    else:
       output += r"\frac{%s}{%s}"%(n,x)
\end{sagesilent}
\noindent $\sagestr{output}$
\end{document}

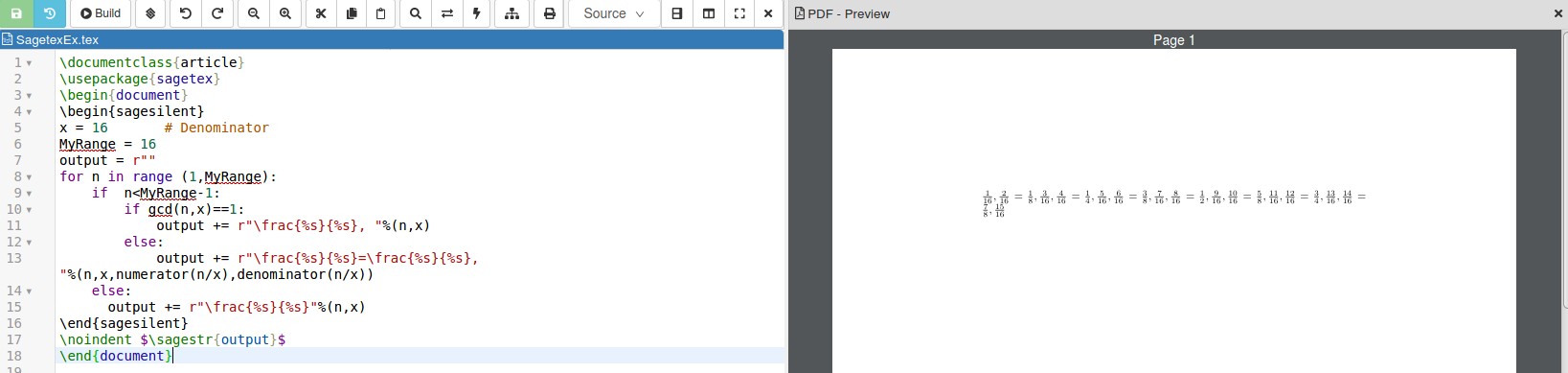
When run using LaTeX this gives the picture below

The approach I used was to see if the numerator and denominator were coprime, if gcd(n,x)==1, in which case output the fraction as is, otherwise typeset fraction and then what it simplifies to, using numerator() and denominator. Finally, to account for the commas and final fraction with no comma after it, I printed out commas until the last term, which I assume was 1 less than MyRange. This seems easier to me because I've avoided the lengthy append you've created when the fraction simplifies.