Revision history [back]

Since you didn't show the first and the second attempt to get g1, we can only guess.

var("x, y")
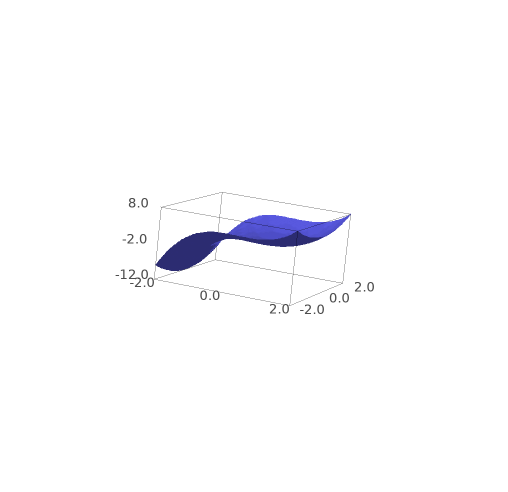
f(x,y)=x^3-x^2+y^2
# BTW, the correct name is "Spectral", not "spectral"...
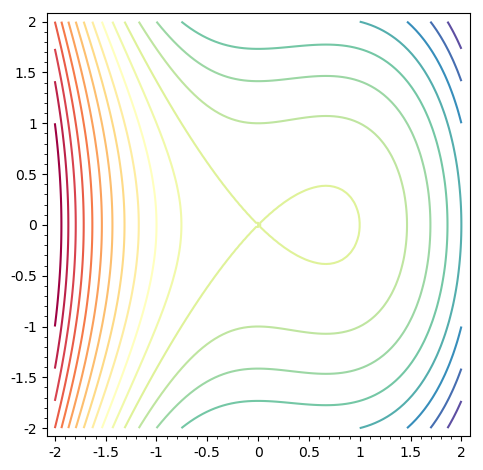
g1 = contour_plot(f(x,y),(x,-2,2),(y,-2,2),
                  contours=20,fill=False,cmap='Spectral')
g1prime = contour_plot(f(x,y),(x,-2,6),(y,-2,4),
                       contours=[1/10,1/2,4/5,1,2,3],cmap='Spectral',fill=False)

for me, g1 is

and g1prime is

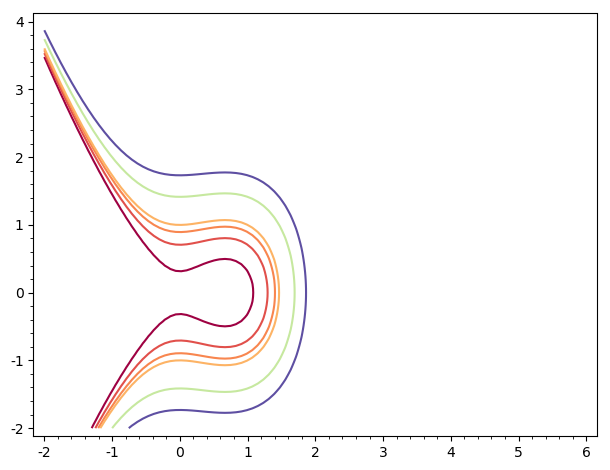
They are obviously different, since you changed:

• the ranges, and
• the contours specification.

Now, adding

g2=plot_vector_field(f.gradient(), (x, -2, 2), (y, -2, 2))

to the first graph (same range specification) gives me

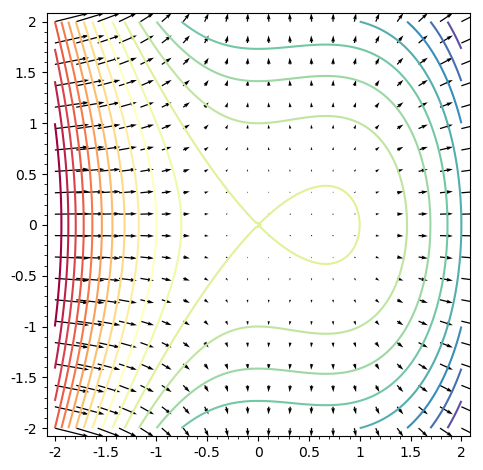
which does not look that unreasonable...

Since you didn't show the first and the second attempt to get g1, we can only guess.

var("x, y")
f(x,y)=x^3-x^2+y^2
# BTW, the correct name is "Spectral", not "spectral"...
g1 = contour_plot(f(x,y),(x,-2,2),(y,-2,2),
                  contours=20,fill=False,cmap='Spectral')
g1prime = contour_plot(f(x,y),(x,-2,6),(y,-2,4),
                       contours=[1/10,1/2,4/5,1,2,3],cmap='Spectral',fill=False)

for me, g1 is

and g1prime is

They are obviously different, since you changed:

• the ranges, and
• the contours specification.

Now, adding

g2=plot_vector_field(f.gradient(), (x, -2, 2), (y, -2, 2))

to the first graph (same range specification) gives me

which does not look that unreasonable...