Revision history [back]

I will provide a parcial answer to the question. Let us consider the following LaTeX code:

\documentclass[12pt]{article}
\usepackage[T1]{fontenc}
\usepackage[utf8]{inputenc}
\usepackage[spanish,es-noshorthands]{babel}
\usepackage{amsmath}
\usepackage{siunitx}
\usepackage{sagetex}

\begin{document}

\begin{sagesilent}
def NumWrap(number):
    if number in ZZ or number.parent()==QQ:
        return r"\num{"+ str(number) + "}"
    else:
        return r"\num{"+ str(float(number)) + "}" 

def MatWrap(m):
    s = r"\begin{pmatrix} " 
    for nrow in range(m.nrows()):
        for ncol in range(m.ncols()-1):
            s += NumWrap(m[nrow,ncol]) + " & "
        s += NumWrap(m[nrow,-1])
        if nrow<m.nrows()-1: s += r" \\ "
    s += r" \end{pmatrix}"
    return s
\end{sagesilent}

Let us do a few operations with integers:
\begin{equation*}
   \num{125}\times\num{8750}+\num{93251} = \sagestr{NumWrap(125*8750+93251)}.
\end{equation*}
Now, we operate with fractions, first in display math mode:
\begin{equation*}
   \sisetup{quotient-mode = fraction}
   \num{12985/3425} + \num{100000/625}
   = \sagestr{NumWrap(12985/3425+100000/625)},
\end{equation*}
and now in inline math mode:
$\num{12985/3425} + \num{100000/625}=\sagestr{NumWrap(12985/3425+100000/625)}$.

It is the turn for floating point numbers and matrices.
\begin{sagesilent}
m = matrix([[12.3456, 2.3453456],[-987654.32456, 23145.5342]])
\end{sagesilent}
Let
\begin{equation*}
   M = \sagestr{MatWrap(m)}.
\end{equation*}
Then, 
\begin{equation*}
   M^{-1} = \sagestr{MatWrap(m.inverse())}.
\end{equation*}

\end{document}

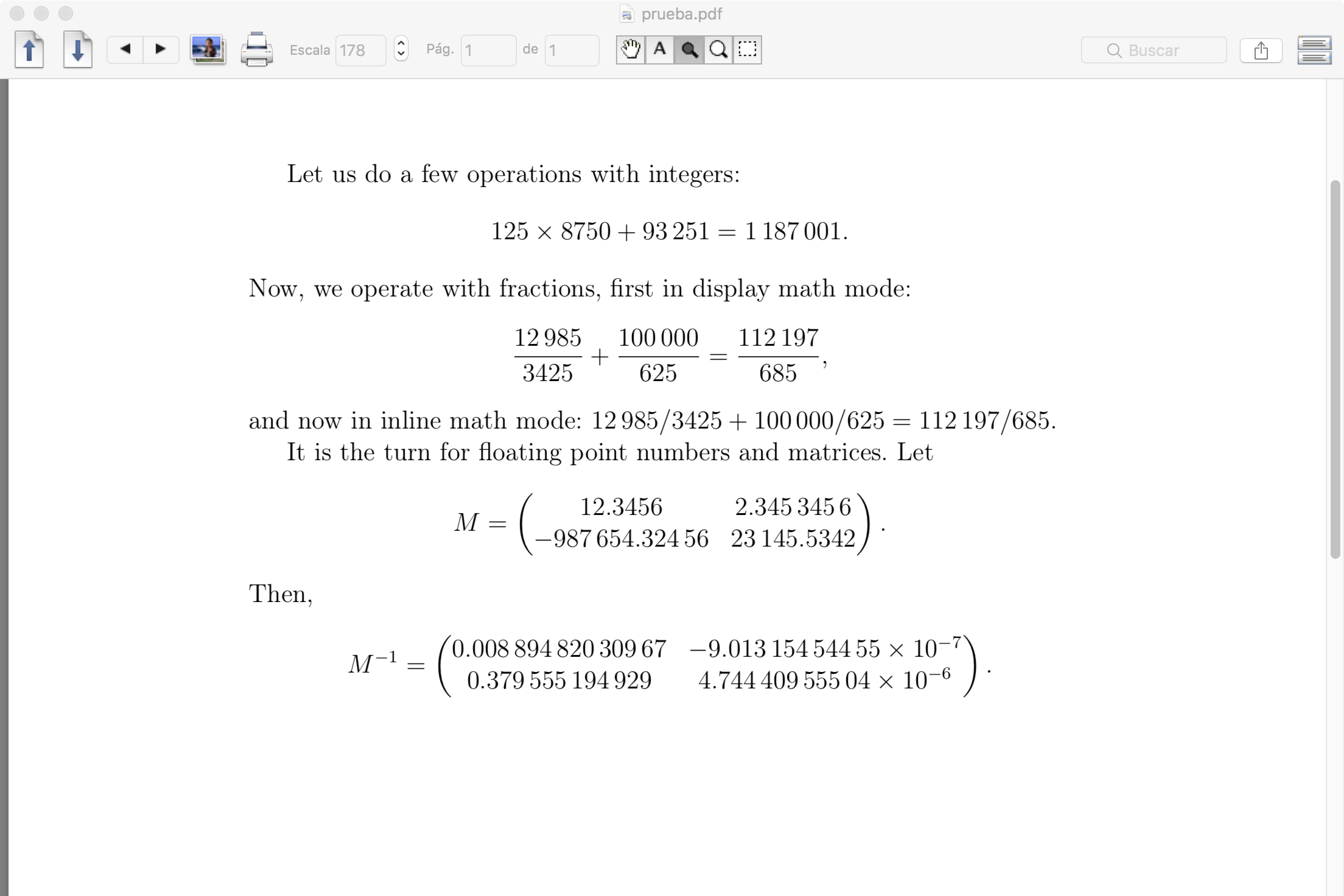
Suppose that x is a number coming from a Sage computation that we want to include in the LaTeX document. The Sage function NumWrap takes a string representation of this number and returns the string \num{str(x)}. This string is passed from Sage to LaTeX by the \sagestr macro, so it can be typeset. For a matrix, MatWrap applies NumWrap to each element and adds LaTeX code to get a pmatrix environment (defined in the amsmath package). I adjoin a screen capture of the document obtained after typesetting the above LaTeX code.