Revision history [back]

Hello, again, @stockh0lm. You post questions that are really challenging; this one took me various hours. Most of the things that you want to do, Sage does not do by default (I think). You must be doing an amazing research! I had to extract a bit of code from SageMath, and modify it, but this will do the trick.

You have to replace the last two lines of your code with the following:

import matplotlib.pyplot as mpl
fig = mpl.figure(pic._figsize)
for i, g in zip(range(1, 5), pic._glist):
    subplot = mpl.subplot(2, 2, i)
    g.matplotlib(figure=fig, sub=subplot, verify=True, axes=True, frame=True)

This is basically the code at the heart of the subroutine that plots a graphics_array, so nothing extra has been added so far. The meaning of almost every sentence here can be deduced from my previous answer

The new thing we are going to add is the following:

fig.text(0.5, 0.0, '$z_c$ in [m]', horizontalalignment='center', fontsize=15)
fig.text(0.0, 0.5, '$\\varphi$ in [V]', horizontalalignment='center', rotation=90, fontsize=15)

These are simple text drawing subroutines from Matplotlib. We are telling to add the text to the figure represented by fig, which we created before. Did you notice the coordinates I used? They are absolute coordinates, i.e., they are normalized from 0 to 1. So, when I say 0.5, 0.0 in the first text() command, I am indicating the center of the $x$- axis. The horizontal alignment='center'argument tells Matplotlib center the text at this point. The rotation (in the second text() command) and fontsize options are self-explaining.

Now we save the plot:

g.save('test.png', figure=fig, sub=subplot, verify=True, axes=True, frame=True)

You may have noticed that I indicated axes=True, frame=True in the first chunk of code as in this last line. I don't know why, but if you exclude one of them, the results are quite strange. For example, deleting these options in the last line draws axes and frames for the first 3 plots, but the last one only has axes. Maybe somebody more experienced with SageMath (or more intelligent) than me can explain this.

Anyway, the result should look like this:

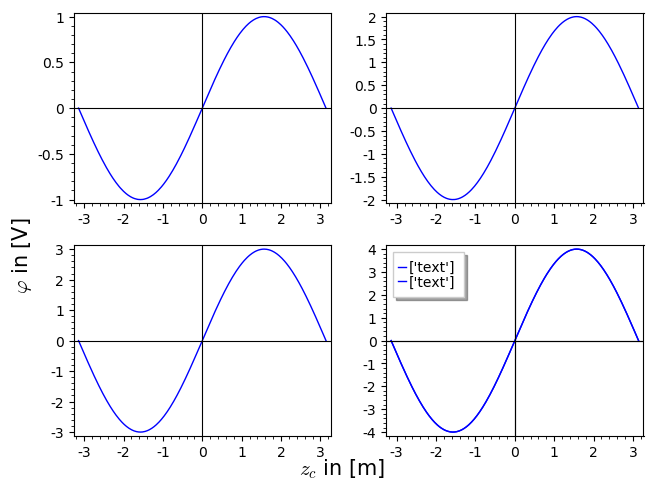
As always, I add a link to a Sage Cell with my code.

I hope this helps!

Hello, again, @stockh0lm. You post questions that are really challenging; this one took me various hours. Most of the things that you want to do, Sage does not do by default (I think). You must be doing an amazing research! I had to extract a bit of code from SageMath, and modify it, but this will do the trick.

You have to replace the last two lines of your code with the following:

import matplotlib.pyplot as mpl
fig = mpl.figure(pic._figsize)
for i, g in zip(range(1, 5), pic._glist):
    subplot = mpl.subplot(2, 2, i)
    # All plots use the same $y$ scale:
    g.matplotlib(figure=fig, sub=subplot, verify=True, axes=True, frame=True)
frame=True, ymin=ym, ymax=yM)

This is basically the code at the heart of the subroutine that plots a graphics_array, so nothing extra has been added so far. The meaning of almost every sentence here can be deduced from my previous answer, but the imprtant part is we are using your ym and yM as our ymin and ymax, respectively.

The new thing we are going to add is the following:

fig.text(0.5, 0.0, '$z_c$ in [m]', horizontalalignment='center', fontsize=15)
fig.text(0.0, 0.5, '$\\varphi$ in [V]', horizontalalignment='center', rotation=90, fontsize=15)

These are simple text drawing subroutines from Matplotlib. We are telling to add the text to the figure represented by fig, which we created before. Did you notice the coordinates I used? They are absolute coordinates, i.e., they are normalized from 0 to 1. So, when I say 0.5, 0.0 in the first text() command, I am indicating the center of the $x$- axis. The horizontal alignment='center'argument tells Matplotlib center the text at this point. The rotation (in the second text() command) and fontsize options are self-explaining.

Now we save the plot:

g.save('test.png', figure=fig, sub=subplot, verify=True, axes=True, frame=True)

You may have noticed that I indicated axes=True, frame=True in the first chunk of code as in this last line. I don't know why, but if you exclude one of them, the results are quite strange. For example, deleting these options in the last line draws axes and frames for the first 3 plots, but the last one only has axes. Maybe somebody more experienced with SageMath (or more intelligent) than me can explain this.

Anyway, the result should look like this:

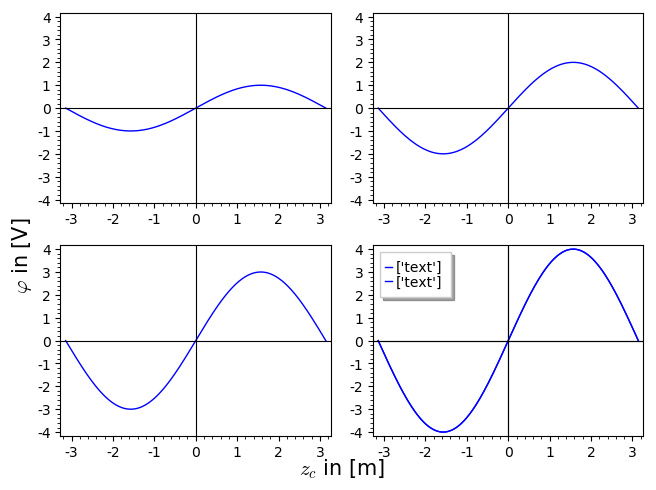
As always, I add a link permalink to a Sage Cell with my the corresponding code.

I hope this helps!

Hello, again, @stockh0lm. You post questions that are really challenging; this one took me various hours. Most of the things that you want to do, Sage does not do by default (I think). You must be doing an amazing research! I had to extract a bit of code from SageMath, and modify it, but this will do the trick.

You We will start by creating the plots you need, and wrapping them inside a list 'l':

l = []
k = 1.0
p = plot(k*sin(x),(x,-pi,pi), legend_label='text')
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi))
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi))
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi))
l.append(p)

Notice I have to replace the last two lines of your code used the legend_label option in the first plot, because putting it in any other of the plots, causes duplicated legends (really don't know why, but it seems to be related to the way SageMath interfaces with the following:Matplotlib).

Now, we are going to convert the plots to Matplotlib format with the following code:

import matplotlib.pyplot as mpl
fig = mpl.figure(pic._figsize)
mpl.figure()
for i, g in zip(range(1, 5), pic._glist):
    subplot = mpl.subplot(2, 2, i)
    # All plots use the same $y$ scale:
    g.matplotlib(figure=fig, sub=subplot, verify=True, axes=True, frame=True, ymin=ym, ymax=yM)
ymax=yM, gridlines='major')

This is basically the code at the heart of the subroutine that plots a graphics_array, (similiar to our variable l), so nothing extra has been added so far. The meaning of almost every sentence here can be deduced from my previous answer, but the imprtant important part is we are using your ym and yM as our ymin and ymax, respectively.

The new thing we are going to add is the following:

fig.text(0.5, 0.0, '$z_c$ in [m]', horizontalalignment='center', fontsize=15)
fig.text(0.0, 0.5, '$\\varphi$ in [V]', horizontalalignment='center', rotation=90, fontsize=15)

These are simple text drawing subroutines from Matplotlib. We are telling to add the text to the figure represented by fig, which we created before. Did you notice the coordinates I used? They are absolute coordinates, i.e., they are normalized from 0 to 1. So, when I say 0.5, 0.0 in the first text() command, I am indicating the center of the $x$- axis. The horizontal alignment='center'argument tells Matplotlib center the text at this point. The rotation (in the second text() command) and fontsize options are self-explaining.

Now we save the plot:

g.save('test.png', figure=fig, sub=subplot, verify=True, axes=True, frame=True)

You may have noticed that I indicated axes=True, frame=True in the first chunk of code as in this last line. I don't know why, but if you exclude one of them, the results are quite strange. For example, deleting these options in the last line draws axes and frames for the first 3 plots, but the last one only has axes. Maybe somebody more experienced with SageMath (or more intelligent) than me can explain this.

Anyway, the result should look like this:

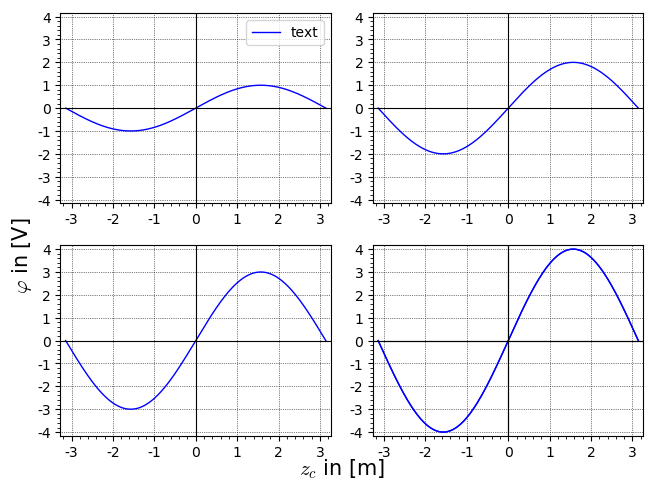
As always, I add a permalink to a Sage Cell with the corresponding code.

I hope this helps!

Hello, again, @stockh0lm. You post questions that are really challenging; this one took me various hours. Most of the things that you want to do, Sage does not do by default (I think). You must be doing an amazing research! I had to extract a bit of code from SageMath, and modify it, but this will do the trick.

We will start by creating the plots you need, and wrapping them inside a list 'l':

l = []
k = 1.0
p = plot(k*sin(x),(x,-pi,pi), legend_label='text')
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi))
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi))
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi))
l.append(p)

Notice I have used the legend_label option in the first plot, because putting it in any other of the plots, causes duplicated legends (really don't know why, but it seems to be related to the way SageMath interfaces with Matplotlib).

Now, we are going to convert the plots to Matplotlib format with the following code:

import matplotlib.pyplot as mpl
fig = mpl.figure()
for i, g in zip(range(1, 5), pic._glist):
    subplot = mpl.subplot(2, 2, i)
    # All plots use the same $y$ scale:
    g.matplotlib(figure=fig, sub=subplot, verify=True, axes=True, frame=True, ymin=ym, ymax=yM, gridlines='major')

This is basically the code at the heart of the subroutine that plots a graphics_array (similiar to our variable l), so nothing extra has been added so far. The meaning of almost every sentence here can be deduced from my previous answer, but the important part is we are using your ym and yM as our ymin and ymax, respectively.

The new thing we are going to add is the following:

fig.text(0.5, 0.0, '$z_c$ in [m]', horizontalalignment='center', fontsize=15)
fig.text(0.0, 0.5, '$\\varphi$ in [V]', horizontalalignment='center', rotation=90, fontsize=15)

These are simple text drawing subroutines from Matplotlib. We are telling to add the text to the figure represented by fig, which we created before. Did you notice the coordinates I used? They are absolute coordinates, i.e., they are normalized from 0 to 1. So, when I say 0.5, 0.0 in the first text() command, I am indicating the center of the $x$- axis. The horizontal alignment='center'argument tells Matplotlib center the text at this point. The rotation (in the second text() command) and fontsize options are self-explaining.

Now we save the plot:

g.save('test.png', figure=fig, sub=subplot, verify=True, axes=True, frame=True)

You may have noticed that I indicated axes=True, frame=True in the first chunk of code as in this last line. I don't know why, but if you exclude one of them, the results are quite strange. For example, deleting these options in the last line draws axes and frames for the first 3 plots, but the last one only has axes. Maybe somebody more experienced with SageMath (or more intelligent) than me can explain this.

Anyway, the result should look like this:

As always, I add a permalink to a Sage Cell with the corresponding code.

I hope this helps!

Hello, again, @stockh0lm. You post questions that are really challenging; this one took me various hours. Most of the things that you want to do, Sage does not do by default (I think). You must be doing an amazing research! I had to extract a bit of code from SageMath, and modify it, but this will do the trick.

We will start by creating the plots you need, and wrapping them inside a list 'l':

l = []
k = 1.0
p = plot(k*sin(x),(x,-pi,pi), legend_label='text')
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi))
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi))
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi))
l.append(p)

Notice I have used the legend_label option in the first plot, because putting it in any other of the plots, causes duplicated legends (really don't know why, but it seems to be related to the way SageMath interfaces with Matplotlib).

Now, we are going to convert the plots to Matplotlib format with the following code:

import matplotlib.pyplot as mpl
fig = mpl.figure()
for i, g in zip(range(1, 5), pic._glist):
    subplot = mpl.subplot(2, 2, i)
    # All plots use the same $y$ scale:
    g.matplotlib(figure=fig, sub=subplot, verify=True, axes=True, frame=True, ymin=ym, ymax=yM, gridlines='major')

This is basically the code at the heart of the subroutine that plots a graphics_array (similiar to our variable l), so nothing extra has been added so far. The meaning of almost every sentence here can be deduced from my previous answer, but the important part is we are using your ym and yM as our ymin and ymax, respectively.

The new thing we are going to add is the following:

fig.text(0.5, 0.0, '$z_c$ in [m]', horizontalalignment='center', fontsize=15)
fig.text(0.0, 0.5, '$\\varphi$ in [V]', horizontalalignment='center', rotation=90, fontsize=15)

These are simple text drawing subroutines from Matplotlib. We are telling to add the text to the figure represented by fig, which we created before. Did you notice the coordinates I used? They are absolute coordinates, i.e., they are normalized from 0 to 1. So, when I say 0.5, 0.0 in the first text() command, I am indicating the center of the $x$- axis. The horizontal alignment='center'argument tells Matplotlib center the text at this point. The rotation (in the second text() command) and fontsize options are self-explaining.

Now we save the plot:

g.save('test.png', figure=fig, sub=subplot, verify=True, axes=True, frame=True)

You may have noticed that I indicated axes=True, frame=True in the first chunk of code as in this last line. I don't know why, but if you exclude one of them, the results are quite strange. For example, deleting these options in the last line draws axes and frames for the first 3 plots, but the last one only has axes. Maybe somebody more experienced with SageMath (or more intelligent) than me can explain this.

Anyway, the result should look like this:

As always, I add a permalink to a Sage Cell with the corresponding code.

I hope this helps!

Hello, again, @stockh0lm. You post questions that are really challenging; this one took me various hours. Most of the things that you want to do, Sage does not do by default (I think). You must be doing an amazing research! I had to extract a bit of code from SageMath, and modify it, but this will do the trick.

We will start by creating the plots you need, and wrapping them inside a list 'l':

l = []
k = 1.0
p = plot(k*sin(x),(x,-pi,pi), legend_label='text')
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi))
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi))
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi))
l.append(p)

Notice I have used the legend_label option in the first plot, because putting it in any other of the plots, causes duplicated legends (really don't know why, but it seems to be related to the way SageMath interfaces with Matplotlib).

Now, we are going to convert the plots to Matplotlib format with the following code:

import matplotlib.pyplot as mpl
fig = mpl.figure()
for i, g in zip(range(1, 5), pic._glist):
    subplot = mpl.subplot(2, 2, i)
    # All plots use the same $y$ scale:
    g.matplotlib(figure=fig, sub=subplot, verify=True, axes=True, frame=True, ymin=ym, ymax=yM, gridlines='major')

This is basically the code at the heart of the subroutine that plots a graphics_array (similiar to our variable l), so nothing extra has been added so far. The meaning of almost every sentence here can be deduced from my previous answer, but the important part is we are using your ym and yM as our ymin and ymax, respectively.

The new thing we are going to add is the following:

fig.text(0.5, 0.0, '$z_c$ in [m]', horizontalalignment='center', fontsize=15)
fig.text(0.0, 0.5, '$\\varphi$ in [V]', horizontalalignment='center', rotation=90, fontsize=15)

These are simple text drawing subroutines from Matplotlib. We are telling to add the text to the figure represented by fig, which we created before. Did you notice the coordinates I used? They are absolute coordinates, i.e., they are normalized from 0 to 1. So, when I say 0.5, 0.0 in the first text() command, I am indicating the center of the $x$- axis. The horizontal alignment='center'argument tells Matplotlib center the text at this point. The rotation (in the second text() command) and fontsize options are self-explaining.

Now we save the plot:

g.save('test.png', figure=fig, sub=subplot, verify=True, axes=True, frame=True)

You may have noticed that I indicated axes=True, frame=True in the first chunk of code as in this last line. I don't know why, but if you exclude one of them, the results are quite strange. For example, deleting these options in the last line draws axes and frames for the first 3 plots, but the last one only has axes. Maybe somebody more experienced with SageMath (or more intelligent) than me can explain this.

Anyway, the result should look like this:

As always, I add a permalink to a Sage Cell with the corresponding code.

I just

Hello, again, @stockh0lm. You post questions that are really challenging; this one took me various hours. Most of the things that you want to do, Sage does not do by default (I think). You must be doing an amazing research! I had to extract a bit of code from SageMath, and modify it, but this will do the trick.

We will start by creating the plots you need, and wrapping them inside a list 'l':

l = []
k = 1.0
p = plot(k*sin(x),(x,-pi,pi), legend_label='text')
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi))
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi))
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi))
l.append(p)

Notice I have used the legend_label option in the first plot, because putting it in any other of the plots, causes duplicated legends (really don't know why, but it seems to be related to the way SageMath interfaces with Matplotlib).

Now, we are going to convert the plots to Matplotlib format with the following code:

import matplotlib.pyplot as mpl
fig = mpl.figure()
for i, g in zip(range(1, 5), pic._glist):
    subplot = mpl.subplot(2, 2, i)
    # All plots use the same $y$ scale:
    g.matplotlib(figure=fig, sub=subplot, verify=True, axes=True, frame=True, ymin=ym, ymax=yM, gridlines='major')

This is basically the code at the heart of the subroutine that plots a graphics_array (similiar to our variable l), so nothing extra has been added so far. The meaning of almost every sentence here can be deduced from my previous answer, but the important part is we are using your ym and yM as our ymin and ymax, respectively.

The new thing we are going to add is the following:

fig.text(0.5, 0.0, '$z_c$ in [m]', horizontalalignment='center', fontsize=15)
fig.text(0.0, 0.5, '$\\varphi$ in [V]', horizontalalignment='center', rotation=90, fontsize=15)

These are simple text drawing subroutines from Matplotlib. We are telling to add the text to the figure represented by fig, which we created before. Did you notice the coordinates I used? They are absolute coordinates, i.e., they are normalized from 0 to 1. So, when I say 0.5, 0.0 in the first text() command, I am indicating the center of the $x$- axis. The horizontal alignment='center'argument tells Matplotlib center the text at this point. The rotation (in the second text() command) and fontsize options are self-explaining.

Now we save the plot:

g.save('test.png', figure=fig, sub=subplot, verify=True, axes=True, frame=True)

You may have noticed that I indicated axes=True, frame=True in the first chunk of code as in this last line. I don't know why, but if you exclude one of them, the results are quite strange. For example, deleting these options in the last line draws axes and frames for the first 3 plots, but the last one only has axes. Maybe somebody more experienced with SageMath (or more intelligent) than me can explain this.

Anyway, the result should look like this:

As always, I add a permalink to a Sage Cell with the corresponding code.

Update: I just found a way of putting the legend on the lower right plot, so I am posting it as an alternative. What you have to do is use the legend_label=None option for the plot command when: l = [] k = 1.0 p = plot(ksin(x),(x,-pi,pi), legend_label=None) l.append(p) k += 1 p = plot(ksin(x),(x,-pi,pi), legend_label=None) l.append(p) k += 1 p = plot(ksin(x),(x,-pi,pi), legend_label=None) l.append(p) k += 1 p = plot(ksin(x),(x,-pi,pi), legend_label=None) l.append(p)

Once done this, just have to add the following code after the for loop: ax = fig.gca() ax.legend(labels=['text'])

That's it! Here is the result:

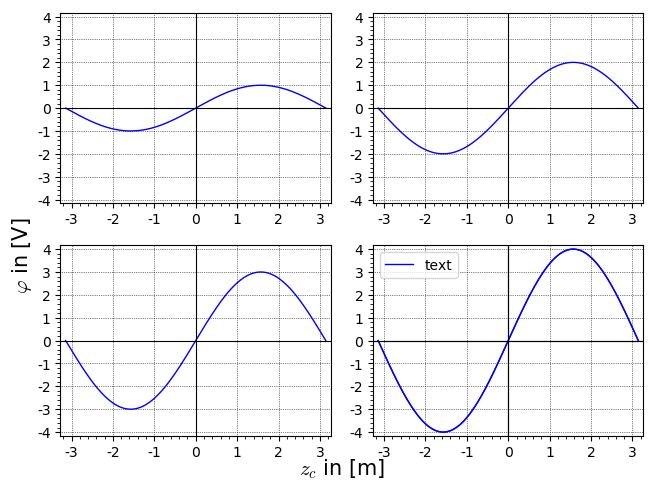result: and here is the corresponding code.

Happy to help! Sorry for the long answer!

Hello, again, @stockh0lm. You post questions that are really challenging; this one took me various hours. Most of the things that you want to do, Sage does not do by default (I think). You must be doing an amazing research! I had to extract a bit of code from SageMath, and modify it, but this will do the trick.

We will start by creating the plots you need, and wrapping them inside a list 'l':

l = []
k = 1.0
p = plot(k*sin(x),(x,-pi,pi), legend_label='text')
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi))
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi))
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi))
l.append(p)

Notice I have used the legend_label option in the first plot, because putting it in any other of the plots, causes duplicated legends (really don't know why, but it seems to be related to the way SageMath interfaces with Matplotlib).

Now, we are going to convert the plots to Matplotlib format with the following code:

import matplotlib.pyplot as mpl
fig = mpl.figure()
for i, g in zip(range(1, 5), pic._glist):
    subplot = mpl.subplot(2, 2, i)
    # All plots use the same $y$ scale:
    g.matplotlib(figure=fig, sub=subplot, verify=True, axes=True, frame=True, ymin=ym, ymax=yM, gridlines='major')

This is basically the code at the heart of the subroutine that plots a graphics_array (similiar to our variable l), so nothing extra has been added so far. The meaning of almost every sentence here can be deduced from my previous answer, but the important part is we are using your ym and yM as our ymin and ymax, respectively.

The new thing we are going to add is the following:

fig.text(0.5, 0.0, '$z_c$ in [m]', horizontalalignment='center', fontsize=15)
fig.text(0.0, 0.5, '$\\varphi$ in [V]', horizontalalignment='center', rotation=90, fontsize=15)

These are simple text drawing subroutines from Matplotlib. We are telling to add the text to the figure represented by fig, which we created before. Did you notice the coordinates I used? They are absolute coordinates, i.e., they are normalized from 0 to 1. So, when I say 0.5, 0.0 in the first text() command, I am indicating the center of the $x$- axis. The horizontal alignment='center'argument tells Matplotlib center the text at this point. The rotation (in the second text() command) and fontsize options are self-explaining.

Now we save the plot:

g.save('test.png', figure=fig, sub=subplot, verify=True, axes=True, frame=True)

You may have noticed that I indicated axes=True, frame=True in the first chunk of code as in this last line. I don't know why, but if you exclude one of them, the results are quite strange. For example, deleting these options in the last line draws axes and frames for the first 3 plots, but the last one only has axes. Maybe somebody more experienced with SageMath (or more intelligent) than me can explain this.

Anyway, the result should look like this:

As always, I add a permalink to a Sage Cell with the corresponding code.

Update: I just found a way of putting the legend on the lower right plot, so I am posting it as an alternative. What you have to do is use the legend_label=None option for the plot command when: l = [] k = 1.0 p = plot(ksin(x),(x,-pi,pi), legend_label=None) l.append(p) k += 1 p = plot(ksin(x),(x,-pi,pi), legend_label=None) l.append(p) k += 1 p = plot(ksin(x),(x,-pi,pi), legend_label=None) l.append(p) k += 1 p = plot(ksin(x),(x,-pi,pi), legend_label=None) l.append(p)

when creating list l. Once done this, just have to add the following code after the for loop: ax = fig.gca() ax.legend(labels=['text'])

That's it! Here is the result: and here is the corresponding code.

Happy to help! Sorry for the long answer!

Hello, again, @stockh0lm. You post questions that are really challenging; this one took me various hours. Most of the things that you want to do, Sage does not do by default (I think). You must be doing an amazing research! I had to extract a bit of code from SageMath, and modify it, but this will do the trick.

We will start by creating the plots you need, and wrapping them inside a list 'l':

l = []
k = 1.0
p = plot(k*sin(x),(x,-pi,pi), legend_label='text')
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi))
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi))
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi))
l.append(p)

Notice I have used the legend_label option in the first plot, because putting it in any other of the plots, causes duplicated legends (really don't know why, but it seems to be related to the way SageMath interfaces with Matplotlib).

Now, we are going to convert the plots to Matplotlib format with the following code:

import matplotlib.pyplot as mpl
fig = mpl.figure()
for i, g in zip(range(1, 5), pic._glist):
    subplot = mpl.subplot(2, 2, i)
    # All plots use the same $y$ scale:
    g.matplotlib(figure=fig, sub=subplot, verify=True, axes=True, frame=True, ymin=ym, ymax=yM, gridlines='major')

This is basically the code at the heart of the subroutine that plots a graphics_array (similiar to our variable l), so nothing extra has been added so far. The meaning of almost every sentence here can be deduced from my previous answer, but the important part is we are using your ym and yM as our ymin and ymax, respectively.

The new thing we are going to add is the following:

fig.text(0.5, 0.0, '$z_c$ in [m]', horizontalalignment='center', fontsize=15)
fig.text(0.0, 0.5, '$\\varphi$ in [V]', horizontalalignment='center', rotation=90, fontsize=15)

These are simple text drawing subroutines from Matplotlib. We are telling to add the text to the figure represented by fig, which we created before. Did you notice the coordinates I used? They are absolute coordinates, i.e., they are normalized from 0 to 1. So, when I say 0.5, 0.0 in the first text() command, I am indicating the center of the $x$- axis. The horizontal alignment='center'argument tells Matplotlib center the text at this point. The rotation (in the second text() command) and fontsize options are self-explaining.

Now we save the plot:

g.save('test.png', figure=fig, sub=subplot, verify=True, axes=True, frame=True)

You may have noticed that I indicated axes=True, frame=True in the first chunk of code as in this last line. I don't know why, but if you exclude one of them, the results are quite strange. For example, deleting these options in the last line draws axes and frames for the first 3 plots, but the last one only has axes. Maybe somebody more experienced with SageMath (or more intelligent) than me can explain this.

Anyway, the result should look like this:

As always, I add a permalink to a Sage Cell with the corresponding code.

Update: I just found a way of putting the legend on the lower right plot, so I am posting it as an alternative. What you have to do is use the legend_label=None option for the plot command when creating list l. Once done this, just have to add the following code after the for loop: loop:

ax = fig.gca()
    ax.legend(labels=['text'])
ax.legend(labels=['text'])

That's it! Here is the result: and here is the corresponding code.

Happy to help! Sorry for the long answer!

Hello, again, @stockh0lm. You post questions that are really challenging; this one took me various hours. Most of the things that you want to do, Sage does not do by default (I think). You must be doing an amazing research! I had to extract a bit of code from SageMath, and modify it, but this will do the trick.

We will start by creating the plots you need, and wrapping them inside a list 'l':

l = []
k = 1.0
p = plot(k*sin(x),(x,-pi,pi), legend_label='text')
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi))
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi))
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi))
l.append(p)

Notice I have used the legend_label option in the first plot, because putting it in any other of the plots, causes duplicated legends (really don't know why, but it seems to be related to the way SageMath interfaces with Matplotlib).

Now, we are going to convert the plots to Matplotlib format with the following code:

import matplotlib.pyplot as mpl
fig = mpl.figure()
for i, g in zip(range(1, 5), pic._glist):
    subplot = mpl.subplot(2, 2, i)
    # All plots use the same $y$ scale:
    g.matplotlib(figure=fig, sub=subplot, verify=True, axes=True, frame=True, ymin=ym, ymax=yM, gridlines='major')

This is basically the code at the heart of the subroutine that plots a graphics_array (similiar to our variable l), so nothing extra has been added so far. The meaning of almost every sentence here can be deduced from my previous answer, but the important part is we are using your ym and yM as our ymin and ymax, respectively.

The new thing we are going to add is the following:

fig.text(0.5, 0.0, '$z_c$ in [m]', horizontalalignment='center', fontsize=15)
fig.text(0.0, 0.5, '$\\varphi$ in [V]', horizontalalignment='center', rotation=90, fontsize=15)

These are simple text drawing subroutines from Matplotlib. We are telling to add the text to the figure represented by fig, which we created before. Did you notice the coordinates I used? They are absolute coordinates, i.e., they are normalized from 0 to 1. So, when I say 0.5, 0.0 in the first text() command, I am indicating the center of the $x$- axis. The horizontal alignment='center'argument tells Matplotlib center the text at this point. The rotation (in the second text() command) and fontsize options are self-explaining.

Now we save the plot:

g.save('test.png', figure=fig, sub=subplot, verify=True, axes=True, frame=True)

You may have noticed that I indicated axes=True, frame=True in the first chunk of code as in this last line. I don't know why, but if you exclude one of them, the results are quite strange. For example, deleting these options in the last line draws axes and frames for the first 3 plots, but the last one only has axes. Maybe somebody more experienced with SageMath (or more intelligent) than me can explain this.

Anyway, the result should look like this:

As always, I add a permalink to a Sage Cell with the corresponding code.

Update: I just found a way of putting the legend on the lower right plot, so I am posting it as an alternative. What you have to do is use the legend_label=None option for the plot command when creating list l. :

l = []
k = 1.0
p = plot(k*sin(x),(x,-pi,pi), legend_label=None)
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi), legend_label=None)
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi), legend_label=None)
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi), legend_label=None)
l.append(p)

Once done this, just have to add the following code after the for loop:

ax = fig.gca()
ax.legend(labels=['text'])

That's it! Here is the result: and here is the corresponding code.

Happy to help! Sorry for the long answer!

Hello, again, @stockh0lm. You post questions that are really challenging; this one took me various hours. Most of the things that you want to do, Sage does not do by default (I think). You must be doing an amazing research! I had to extract a bit of code from SageMath, and modify it, but this will do the trick.

We will start by creating the plots you need, and wrapping them inside a list 'l':

l = []
k = 1.0
p = plot(k*sin(x),(x,-pi,pi), legend_label='text')
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi))
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi))
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi))
l.append(p)

Notice I have used the legend_label option in the first plot, because putting it in any other of the plots, causes duplicated legends (really don't know why, but it seems to be related to the way SageMath interfaces with Matplotlib).

Now, we are going to convert the plots to Matplotlib format with the following code:

import matplotlib.pyplot as mpl
fig = mpl.figure()
for i, g in zip(range(1, 5), pic._glist):
    subplot = mpl.subplot(2, 2, i)
    # All plots use the same $y$ scale:
    g.matplotlib(figure=fig, sub=subplot, verify=True, axes=True, frame=True, ymin=ym, ymax=yM, gridlines='major')

This is basically the code at the heart of the subroutine that plots a graphics_array (similiar to our variable l), so nothing extra has been added so far. The meaning of almost every sentence here can be deduced from my previous answer, but the important part is we are using your ym and yM as our ymin and ymax, respectively.

The new thing we are going to add is the following:

fig.text(0.5, 0.0, '$z_c$ in [m]', horizontalalignment='center', fontsize=15)
fig.text(0.0, 0.5, '$\\varphi$ in [V]', horizontalalignment='center', rotation=90, fontsize=15)

These are simple text drawing subroutines from Matplotlib. We are telling to add the text to the figure represented by fig, which we created before. Did you notice the coordinates I used? They are absolute coordinates, i.e., they are normalized from 0 to 1. So, when I say 0.5, 0.0 in the first text() command, I am indicating the center of the $x$- axis. The horizontal alignment='center'argument tells Matplotlib center the text at this point. The rotation (in the second text() command) and fontsize options are self-explaining.

Now we save the plot:

g.save('test.png', figure=fig, sub=subplot, verify=True, axes=True, frame=True)

You may have noticed that I indicated axes=True, frame=True in the first chunk of code as in this last line. I don't know why, but if you exclude one of them, the results are quite strange. For example, deleting these options in the last line draws axes and frames for the first 3 plots, but the last one only has axes. Maybe somebody more experienced with SageMath (or more intelligent) than me can explain this.

Anyway, the result should look like this:

As always, I add a permalink to a Sage Cell with the corresponding code.

Update: I just found a way of putting the legend on the lower right plot, so I am posting it as an alternative. What you have to do is to use the legend_label=None option for the plot command commands when creating the list l:

l = []
k = 1.0
p = plot(k*sin(x),(x,-pi,pi), legend_label=None)
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi), legend_label=None)
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi), legend_label=None)
l.append(p)
k += 1
p = plot(k*sin(x),(x,-pi,pi), legend_label=None)
l.append(p)

Once done this, you just have to add the following code after the for loop:

ax = fig.gca()
ax.legend(labels=['text'])

That's it! Here is the result: and here is the corresponding code.

Happy to help! Sorry for the long answer!