Revision history [back]

Perhaps you could stick to the symbolic ring and compute the gradient just with phi_ges.gradient([x,z]). It is quite fast. Then you can grasp how the gradient is by displaying both components of the gradient vector. The second component is a bit "terrific", but the first one is quite human readable as shown in the following screen capture:

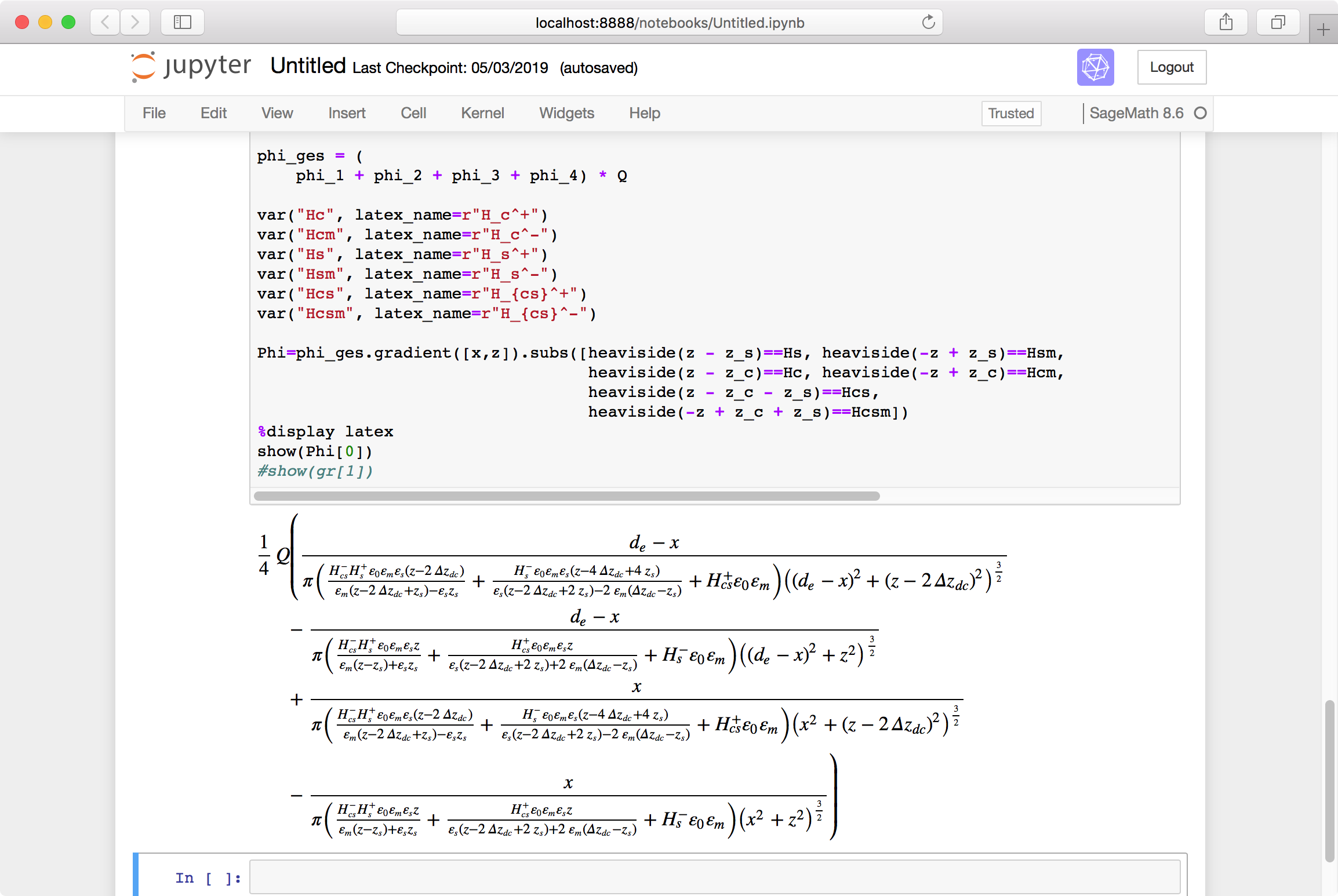
Please note that $H^+_s$, $H^-_s$ and so on represent Heaviside functions evaluated at different arguments (see the var functions and the subs method in the picture). I wonder if this expression can be really simplified.