Revision history [back]
 | 1 | initial version |
I think you want to use RecursivelyEnumerateSet in sage:
sage: v = matrix(4,1,(1,0,0,0))
sage: v.set_immutable()
sage: seed = [v]
sage: thin_group = [random_matrix(ZZ,4,4) for _ in range(5)]
sage: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: ans.append(m_u)
....: return ans
....:
sage: R = RecursivelyEnumeratedSet(seed, succ, max_depth=3)
sage: G = R.to_digraph()
sage: G
Looped multi-digraph on 781 vertices
Then, you may want to use my optional package to visualize it:
sage -pip install slabbe
and then:
sage: from slabbe import TikzPicture
sage: tikz = TikzPicture.from_graph(G)
sage: tikz.pdf()
If your structure is really a tree (or a forest), then use
sage: R = RecursivelyEnumeratedSet(seed, succ, structure='forest')
which will allow you to enumerate the vectors in parallel using map reduce algorithms written by Florent Hivert. In any case, first consult the documentation I have written:
sage: RecursivelyEnumeratedSet?
In any case, tell me if you have any comment, I intend to improve this module in a near future.
 | 2 | No.2 Revision |
I think you want to use RecursivelyEnumerateSet in sage:
sage: v = matrix(4,1,(1,0,0,0))
sage: v.set_immutable()
sage: seed = [v]
sage: thin_group = [random_matrix(ZZ,4,4) for _ in range(5)]
sage: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: ans.append(m_u)
....: return ans
....:
sage: R = RecursivelyEnumeratedSet(seed, succ, max_depth=3)
sage: G = R.to_digraph()
sage: G
Looped multi-digraph on 781 vertices
You may also use a hmax variable instead of using max_depth if you prefer :
sage: hmax = 50
sage: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: if max(map(abs, m_u)) < hmax:
....: ans.append(m_u)
....: return ans
....:
sage: R = RecursivelyEnumeratedSet(seed, succ)
sage: G = R.to_digraph()
sage: G
Looped multi-digraph on 67 vertices
Then, you may want to use my optional package to visualize it:
sage -pip install slabbe
and then:
sage: from slabbe import TikzPicture
sage: tikz = TikzPicture.from_graph(G)
sage: tikz.pdf()
If your structure is really a tree (or a forest), then use
sage: R = RecursivelyEnumeratedSet(seed, succ, structure='forest')
which will allow you to enumerate the vectors in parallel using map reduce algorithms written by Florent Hivert. In any case, first consult the documentation I have written:
sage: RecursivelyEnumeratedSet?
In any case, tell Tell me if you have any comment, I intend to improve this module in a near future.
 | 3 | No.3 Revision |
I think you want to use RecursivelyEnumerateSet in sage:
sage: v = matrix(4,1,(1,0,0,0))
sage: v.set_immutable()
sage: seed = [v]
sage: thin_group = [random_matrix(ZZ,4,4) for _ in range(5)]
sage: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: ans.append(m_u)
....: return ans
....:
sage: R = RecursivelyEnumeratedSet(seed, succ, max_depth=3)
sage: G = R.to_digraph()
sage: G
Looped multi-digraph on 781 vertices
You may also use a hmax variable instead of using max_depth if you prefer :
sage: hmax = 50
sage: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: if max(map(abs, m_u)) < hmax:
....: ans.append(m_u)
....: return ans
....:
sage: R = RecursivelyEnumeratedSet(seed, succ)
sage: G = R.to_digraph()
sage: G
Looped multi-digraph on 67 vertices
Then, you may want to use my optional package to visualize it:it (with dot2tex and graphviz installed):
sage -pip install slabbe
sage -i dot2tex
and then:
sage: from slabbe import TikzPicture
sage: tikz = TikzPicture.from_graph(G)
sage: tikz.pdf()
If your structure is really a tree (or a forest), then use
sage: R = RecursivelyEnumeratedSet(seed, succ, structure='forest')
which will allow you to enumerate the vectors in parallel using map reduce algorithms written by Florent Hivert. In any case, first consult the documentation I have written:
sage: RecursivelyEnumeratedSet?
Tell me if you have any comment, I intend to improve this module in a near future.
 | 4 | No.4 Revision |
I think you want to use RecursivelyEnumerateSet in sage:
sage: v = matrix(4,1,(1,0,0,0))
sage: v.set_immutable()
sage: seed = [v]
sage: thin_group = [random_matrix(ZZ,4,4) for _ in range(5)]
sage: def the_rec_enum_set(hmax):
....: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: ans.append(m_u)
....: return ans
....:
sage: R = RecursivelyEnumeratedSet(seed, succ, max_depth=3)
sage: G = R.to_digraph()
sage: G
Looped multi-digraph on 781 vertices
You may also use a hmax variable instead of using max_depth if you prefer :
sage: hmax = 50
sage: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: if max(map(abs, m_u)) < hmax:
....: ans.append(m_u)
....: return ans
....:
sage: R = RecursivelyEnumeratedSet(seed, succ)
....: return R
....:
sage: G = R.to_digraph()
sage: the_rec_enum_set(50).to_digraph(); G
Looped multi-digraph on 67 37 vertices
sage: G = the_rec_enum_set(500).to_digraph(); G
Looped multi-digraph on 775 vertices
sage: G = the_rec_enum_set(20).to_digraph(): G
Looped multi-digraph on 10 vertices
You may want to use max_depth instead of hmax:
sage: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: ans.append(m_u)
....: return ans
....:
sage: R = RecursivelyEnumeratedSet(seed, succ, max_depth=4)
sage: G = R.to_digraph()
sage: G
Looped multi-digraph on 683 vertices
Then, you may want to use my optional package to visualize it (with dot2tex and graphviz installed):
sage -pip install slabbe
sage -i dot2tex
and then:
sage: from slabbe import TikzPicture
sage: tikz = TikzPicture.from_graph(G)
sage: tikz.pdf()
If your structure is really a tree (or a forest), then use
sage: R = RecursivelyEnumeratedSet(seed, succ, structure='forest')
which will allow you to enumerate the vectors in parallel using map reduce algorithms written by Florent Hivert. In any case, first consult the documentation I have written:
sage: RecursivelyEnumeratedSet?
Tell me if you have any comment, I intend to improve this module in a near future.
 | 5 | No.5 Revision |
I think you want to use RecursivelyEnumerateSet in sage:
sage: v = matrix(4,1,(1,0,0,0))
sage: v.set_immutable()
sage: seed = [v]
sage: thin_group = [random_matrix(ZZ,4,4) for _ in range(5)]
sage: def the_rec_enum_set(hmax):
....: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: if max(map(abs, m_u)) < hmax:
....: ans.append(m_u)
....: return ans
....: R = RecursivelyEnumeratedSet(seed, succ)
....: return R
....:
sage: the_rec_enum_set(20)
A recursively enumerated set (breadth first search)
The recursively enumerated set can be enumerated in different maner (look at the documentation). What I like the most is to create the generated graph:
sage: G = the_rec_enum_set(20).to_digraph(): G
Looped multi-digraph on 10 vertices
sage: G = the_rec_enum_set(50).to_digraph(); G
Looped multi-digraph on 37 vertices
sage: G = the_rec_enum_set(500).to_digraph(); G
Looped multi-digraph on 775 vertices
sage: G = the_rec_enum_set(20).to_digraph(): G
Looped multi-digraph on 10 vertices
The above numbers confirm what dan_fulea obtain.
You may want to use max_depth instead of hmax:
sage: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: ans.append(m_u)
....: return ans
....:
sage: R = RecursivelyEnumeratedSet(seed, succ, max_depth=4)
sage: G = R.to_digraph()
sage: G
Looped multi-digraph on 683 vertices
Then, you may want to use my optional package to visualize it (with dot2tex and graphviz installed):
sage -pip install slabbe
sage -i dot2tex
and then:
sage: from slabbe import TikzPicture
sage: tikz = TikzPicture.from_graph(G)
sage: tikz.pdf()
If your structure is really a tree (or a forest), then use
sage: R = RecursivelyEnumeratedSet(seed, succ, structure='forest')
which will allow you to enumerate the vectors in parallel using map reduce algorithms written by Florent Hivert. In any case, first consult the documentation I have written:
sage: RecursivelyEnumeratedSet?
Tell me if you have any comment, I intend to improve this module in a near future.
 | 6 | No.6 Revision |
I think you want to use RecursivelyEnumerateSetRecursivelyEnumeratedSet in sage:
sage: v = matrix(4,1,(1,0,0,0))
sage: v.set_immutable()
sage: seed = [v]
sage: thin_group = [random_matrix(ZZ,4,4) for _ in range(5)]
sage: def the_rec_enum_set(hmax):
....: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: if max(map(abs, m_u)) < hmax:
....: ans.append(m_u)
....: return ans
....: R = RecursivelyEnumeratedSet(seed, succ)
....: return R
....:
sage: the_rec_enum_set(20)
A recursively enumerated set (breadth first search)
The recursively enumerated set can be enumerated in different maner (look at the documentation). What I like the most is to create the generated graph:
sage: G = the_rec_enum_set(20).to_digraph(): G
Looped multi-digraph on 10 vertices
sage: G = the_rec_enum_set(50).to_digraph(); G
Looped multi-digraph on 37 vertices
sage: G = the_rec_enum_set(500).to_digraph(); G
Looped multi-digraph on 775 vertices
The above numbers confirm what dan_fulea obtain.
You may want to use max_depth instead of hmax:
sage: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: ans.append(m_u)
....: return ans
....:
sage: R = RecursivelyEnumeratedSet(seed, succ, max_depth=4)
sage: G = R.to_digraph()
sage: G
Looped multi-digraph on 683 vertices
Then, you may want to use my optional package to visualize it (with dot2tex and graphviz installed):
sage -pip install slabbe
sage -i dot2tex
and then:
sage: from slabbe import TikzPicture
sage: tikz = TikzPicture.from_graph(G)
sage: tikz.pdf()
If your structure is really a tree (or a forest), then use
sage: R = RecursivelyEnumeratedSet(seed, succ, structure='forest')
which will allow you to enumerate the vectors in parallel using map reduce algorithms written by Florent Hivert. In any case, first consult the documentation I have written:
sage: RecursivelyEnumeratedSet?
Tell me if you have any comment, I intend to improve this module in a near future.
 | 7 | No.7 Revision |
I think you want to use RecursivelyEnumeratedSet in sage:
sage: v = matrix(4,1,(1,0,0,0))
sage: v.set_immutable()
sage: seed = [v]
sage: thin_group = [random_matrix(ZZ,4,4) for _ in range(5)]
sage: def the_rec_enum_set(hmax):
....: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: if max(map(abs, m_u)) < hmax:
....: ans.append(m_u)
....: return ans
....: R = RecursivelyEnumeratedSet(seed, succ)
....: return R
....:
sage: the_rec_enum_set(20)
A recursively enumerated set (breadth first search)
The recursively enumerated set can be enumerated in different maner (look at the documentation). What I like the most is to create the generated graph:
sage: G = the_rec_enum_set(20).to_digraph(): the_rec_enum_set(20).to_digraph(); G
Looped multi-digraph on 10 vertices
sage: G = the_rec_enum_set(50).to_digraph(); G
Looped multi-digraph on 37 vertices
sage: G = the_rec_enum_set(500).to_digraph(); G
Looped multi-digraph on 775 vertices
The above numbers confirm what dan_fulea obtain.
You may want to use max_depth instead of hmax:
sage: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: ans.append(m_u)
....: return ans
....:
sage: R = RecursivelyEnumeratedSet(seed, succ, max_depth=4)
sage: G = R.to_digraph()
sage: G
Looped multi-digraph on 683 vertices
Then, you may want to use my optional package to visualize it (with dot2tex and graphviz installed):
sage -pip install slabbe
sage -i dot2tex
and then:
sage: from slabbe import TikzPicture
sage: tikz = TikzPicture.from_graph(G)
sage: tikz.pdf()
If your structure is really a tree (or a forest), then use
sage: R = RecursivelyEnumeratedSet(seed, succ, structure='forest')
which will allow you to enumerate the vectors in parallel using map reduce algorithms written by Florent Hivert. In any case, first consult the documentation I have written:
sage: RecursivelyEnumeratedSet?
Tell me if you have any comment, I intend to improve this module in a near future.
 | 8 | No.8 Revision |
I think you want to use RecursivelyEnumeratedSet in sage:
sage: v = matrix(4,1,(1,0,0,0))
sage: v.set_immutable()
sage: seed = [v]
sage: thin_group = [random_matrix(ZZ,4,4) for _ in range(5)]
sage: def the_rec_enum_set(hmax):
....: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: if max(map(abs, m_u)) < hmax:
....: ans.append(m_u)
....: return ans
....: R = RecursivelyEnumeratedSet(seed, succ)
....: return R
....:
sage: the_rec_enum_set(20)
A recursively enumerated set (breadth first search)
The recursively enumerated set can be enumerated in different maner (look at the documentation). What I like the most is to create the generated graph:
sage: G = the_rec_enum_set(20).to_digraph(); G
Looped multi-digraph on 10 vertices
sage: G = the_rec_enum_set(50).to_digraph(); G
Looped multi-digraph on 37 vertices
sage: G = the_rec_enum_set(500).to_digraph(); G
Looped multi-digraph on 775 vertices
The above numbers confirm what dan_fulea obtain.
You To get a finite graph, you may want to use max_depth instead of hmax:
sage: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: ans.append(m_u)
....: return ans
....:
sage: R = RecursivelyEnumeratedSet(seed, succ, max_depth=4)
sage: G = R.to_digraph()
sage: G
Looped multi-digraph on 683 vertices
Then, you may want to use my optional package to visualize it (with dot2tex and graphviz installed):
sage -pip install slabbe
sage -i dot2tex
and then:
sage: from slabbe import TikzPicture
sage: tikz = TikzPicture.from_graph(G)
sage: tikz.pdf()
If your structure is really a tree (or a forest), then use
sage: R = RecursivelyEnumeratedSet(seed, succ, structure='forest')
which will allow you to enumerate the vectors in parallel using map reduce algorithms written by Florent Hivert. In any case, first consult the documentation I have written:
sage: RecursivelyEnumeratedSet?
Tell me if you have any comment, I intend to improve this module in a near future.
 | 9 | No.9 Revision |
I think you want to use RecursivelyEnumeratedSet in sage:
sage: v = matrix(4,1,(1,0,0,0))
sage: v.set_immutable()
sage: seed = [v]
sage: thin_group = [random_matrix(ZZ,4,4) for _ in range(5)]
sage: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: ans.append(m_u)
....: return ans
....:
sage: R = RecursivelyEnumeratedSet(seed, succ, max_depth=4)
sage: R
A recursively enumerated set (breadth first search) with max_depth=4
To get a finite graph, you may want to use max_depth as above or hmax as you suggest:
sage: def the_rec_enum_set(hmax):
....: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: if max(map(abs, m_u)) < hmax:
....: ans.append(m_u)
....: return ans
....: R = RecursivelyEnumeratedSet(seed, succ)
....: return R
....:
sage: the_rec_enum_set(20)
A recursively enumerated set (breadth first search)
The recursively enumerated set can be enumerated in different maner (look at the documentation). What I like the most is to create the generated graph:
sage: G = the_rec_enum_set(20).to_digraph(); G
Looped multi-digraph on 10 vertices
sage: G = the_rec_enum_set(50).to_digraph(); G
Looped multi-digraph on 37 vertices
sage: G = the_rec_enum_set(500).to_digraph(); G
Looped multi-digraph on 775 vertices
The above numbers confirm what dan_fulea obtain.
To get a finite graph, you may want to use max_depth instead of hmax:
sage: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: ans.append(m_u)
....: return ans
....:
sage: R = RecursivelyEnumeratedSet(seed, succ, max_depth=4)
sage: G = R.to_digraph()
sage: G
Looped multi-digraph on 683 vertices
Then, you may want to use my optional package to visualize it (with dot2tex and graphviz installed):
sage -pip install slabbe
sage -i dot2tex
and then:
sage: from slabbe import TikzPicture
sage: tikz = TikzPicture.from_graph(G)
sage: tikz.pdf()
If your structure is really a tree (or a forest), then use
sage: R = RecursivelyEnumeratedSet(seed, succ, structure='forest')
which will allow you to enumerate the vectors in parallel using map reduce algorithms written by Florent Hivert. In any case, first consult the documentation I have written:
sage: RecursivelyEnumeratedSet?
Tell me if you have any comment, I intend to improve this module in a near future.
 | 10 | No.10 Revision |
I think you want to use RecursivelyEnumeratedSet in sage:
sage: v = matrix(4,1,(1,0,0,0))
sage: v.set_immutable()
sage: seed = [v]
sage: thin_group = [random_matrix(ZZ,4,4) for _ in range(5)]
sage: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: ans.append(m_u)
....: return ans
....:
sage: R = RecursivelyEnumeratedSet(seed, succ, max_depth=4)
sage: R
A recursively enumerated set (breadth first search) with max_depth=4
To get a finite graph, set, you may want to use max_depth as above or hmax as you suggest:
sage: def the_rec_enum_set(hmax):
....: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: if max(map(abs, m_u)) < hmax:
....: ans.append(m_u)
....: return ans
....: R = RecursivelyEnumeratedSet(seed, succ)
....: return R
....:
sage: the_rec_enum_set(20)
A recursively enumerated set (breadth first search)
The recursively enumerated set can be enumerated in different maner (look at the documentation). What I like the most is to create the generated graph:
sage: G = the_rec_enum_set(20).to_digraph(); G
Looped multi-digraph on 10 vertices
sage: G = the_rec_enum_set(50).to_digraph(); G
Looped multi-digraph on 37 vertices
sage: G = the_rec_enum_set(500).to_digraph(); G
Looped multi-digraph on 775 vertices
The above numbers confirm what dan_fulea obtain.
Then, you may want to use my optional package to visualize it (with dot2tex and graphviz installed):
sage -pip install slabbe
sage -i dot2tex
and then:
sage: from slabbe import TikzPicture
sage: tikz = TikzPicture.from_graph(G)
sage: tikz.pdf()
If your structure is really a tree (or a forest), then use
sage: R = RecursivelyEnumeratedSet(seed, succ, structure='forest')
which will allow you to enumerate the vectors in parallel using map reduce algorithms written by Florent Hivert. In any case, first consult the documentation I have written:
sage: RecursivelyEnumeratedSet?
Tell me if you have any comment, I intend to improve this module in a near future.
 | 11 | No.11 Revision |
I think you want to use RecursivelyEnumeratedSet in sage:
sage: v = matrix(4,1,(1,0,0,0))
sage: v.set_immutable()
sage: seed = [v]
sage: T1 = matrix( ZZ, 4, [ -1,0,0,0, 2, 1,0,0, 4,0, 1,0, 4, 0,0, 1 ] )
sage: T2 = matrix( ZZ, 4, [ 1,2,0,0, 0,-1,0,0, 0,4, 1,0, 0, 4,0, 1 ] )
sage: T3 = matrix( ZZ, 4, [ 1,0,1,0, 0, 1,1,0, 0,0,-1,0, 0, 0,0, 1 ] )
sage: T4 = matrix( ZZ, 4, [ 1,6,0,6, 0, 3,0,2, 0,4, 1,4, 0,-4,0,-3 ] )
sage: T5 = matrix( ZZ, 4, [ 3,0,0,2, 6, 1,0,6, 4,0, 1,4, -4, 0,0,-3 ] )
sage: thin_group = [random_matrix(ZZ,4,4) for _ in range(5)]
[T1, T2, T3, T4, T5]
sage: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: ans.append(m_u)
....: return ans
....:
sage: R = RecursivelyEnumeratedSet(seed, succ, max_depth=4)
sage: R
A recursively enumerated set (breadth first search) with max_depth=4
To get a finite set, you may want to use max_depth as above or hmax as you suggest:
sage: def the_rec_enum_set(hmax):
....: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: if max(map(abs, m_u)) < hmax:
....: ans.append(m_u)
....: return ans
....: R = RecursivelyEnumeratedSet(seed, succ)
....: return R
....:
sage: the_rec_enum_set(20)
A recursively enumerated set (breadth first search)
The recursively enumerated set can be enumerated in different maner (look at the documentation). What I like the most is to create the generated graph:
sage: G = the_rec_enum_set(20).to_digraph(); G
Looped multi-digraph on 10 vertices
sage: G = the_rec_enum_set(50).to_digraph(); G
Looped multi-digraph on 37 vertices
sage: G = the_rec_enum_set(500).to_digraph(); G
Looped multi-digraph on 775 vertices
The above numbers confirm what dan_fulea obtain.
Then, you may want to use my optional package to visualize it (with dot2tex and graphviz installed):
sage -pip install slabbe
sage -i dot2tex
and then:
sage: from slabbe import TikzPicture
sage: tikz = TikzPicture.from_graph(G)
sage: tikz.pdf()
If your structure is really a tree (or a forest), then use
sage: R = RecursivelyEnumeratedSet(seed, succ, structure='forest')
which will allow you to enumerate the vectors in parallel using map reduce algorithms written by Florent Hivert. In any case, first consult the documentation I have written:
sage: RecursivelyEnumeratedSet?
Tell me if you have any comment, I intend to improve this module in a near future.
 | 12 | No.12 Revision |
I think you want to use RecursivelyEnumeratedSet in sage:sage which consist in applying iteratively a successor function to a set of initial seeds:
sage: v = matrix(4,1,(1,0,0,0))
sage: v.set_immutable()
sage: seed = [v]
sage: T1 = matrix( ZZ, 4, [ -1,0,0,0, 2, 1,0,0, 4,0, 1,0, 4, 0,0, 1 ] )
sage: T2 = matrix( ZZ, 4, [ 1,2,0,0, 0,-1,0,0, 0,4, 1,0, 0, 4,0, 1 ] )
sage: T3 = matrix( ZZ, 4, [ 1,0,1,0, 0, 1,1,0, 0,0,-1,0, 0, 0,0, 1 ] )
sage: T4 = matrix( ZZ, 4, [ 1,6,0,6, 0, 3,0,2, 0,4, 1,4, 0,-4,0,-3 ] )
sage: T5 = matrix( ZZ, 4, [ 3,0,0,2, 6, 1,0,6, 4,0, 1,4, -4, 0,0,-3 ] )
sage: thin_group = [T1, T2, T3, T4, T5]
sage: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: ans.append(m_u)
....: return ans
....:
sage: R = RecursivelyEnumeratedSet(seed, succ, max_depth=4)
sage: R
A recursively enumerated set (breadth first search) with max_depth=4
To get a finite set, you may want to use max_depth as above or hmax as you suggest:
sage: def the_rec_enum_set(hmax):
....: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: if max(map(abs, m_u)) < hmax:
....: ans.append(m_u)
....: return ans
....: R = RecursivelyEnumeratedSet(seed, succ)
....: return R
....:
sage: the_rec_enum_set(20)
A recursively enumerated set (breadth first search)
The recursively enumerated set can be enumerated in different maner (look at the documentation). What I like the most is to create the generated graph:
sage: G = the_rec_enum_set(20).to_digraph(); G
Looped multi-digraph on 10 vertices
sage: G = the_rec_enum_set(50).to_digraph(); G
Looped multi-digraph on 37 vertices
sage: G = the_rec_enum_set(500).to_digraph(); G
Looped multi-digraph on 775 vertices
The above numbers confirm what dan_fulea obtain.
Then, you may want to use my optional package to visualize it (with dot2tex and graphviz installed):
sage -pip install slabbe
sage -i dot2tex
and then:
sage: from slabbe import TikzPicture
sage: tikz = TikzPicture.from_graph(G)
sage: tikz.pdf()
If your structure is really a tree (or a forest), then use
sage: R = RecursivelyEnumeratedSet(seed, succ, structure='forest')
which will allow you to enumerate the vectors in parallel using map reduce algorithms written by Florent Hivert. In any case, first consult the documentation I have written:
sage: RecursivelyEnumeratedSet?
Tell me if you have any comment, I intend to improve this module in a near future.
 | 13 | No.13 Revision |
I think you want to use RecursivelyEnumeratedSet in sage which consist in applying iteratively a successor function to a set of initial seeds:
sage: v = matrix(4,1,(1,0,0,0))
sage: v.set_immutable()
sage: seed = [v]
sage: T1 = matrix( ZZ, 4, [ -1,0,0,0, 2, 1,0,0, 4,0, 1,0, 4, 0,0, 1 ] )
sage: T2 = matrix( ZZ, 4, [ 1,2,0,0, 0,-1,0,0, 0,4, 1,0, 0, 4,0, 1 ] )
sage: T3 = matrix( ZZ, 4, [ 1,0,1,0, 0, 1,1,0, 0,0,-1,0, 0, 0,0, 1 ] )
sage: T4 = matrix( ZZ, 4, [ 1,6,0,6, 0, 3,0,2, 0,4, 1,4, 0,-4,0,-3 ] )
sage: T5 = matrix( ZZ, 4, [ 3,0,0,2, 6, 1,0,6, 4,0, 1,4, -4, 0,0,-3 ] )
sage: thin_group = [T1, T2, T3, T4, T5]
sage: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: ans.append(m_u)
....: return ans
....:
sage: R = RecursivelyEnumeratedSet(seed, succ, max_depth=4)
sage: R
A recursively enumerated set (breadth first search) with max_depth=4
To get a finite set, you may want to use max_depth as above or hmax as you suggest:
sage: def the_rec_enum_set(hmax):
....: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: if max(map(abs, m_u)) < hmax:
....: ans.append(m_u)
....: return ans
....: R = RecursivelyEnumeratedSet(seed, succ)
....: return R
....:
sage: the_rec_enum_set(20)
A recursively enumerated set (breadth first search)
The recursively enumerated set can be enumerated in different maner (look at the documentation). What I like the most is to create the generated graph:
sage: G = the_rec_enum_set(20).to_digraph(); G
Looped multi-digraph on 10 vertices
sage: G = the_rec_enum_set(50).to_digraph(); G
Looped multi-digraph on 37 vertices
sage: G = the_rec_enum_set(500).to_digraph(); G
Looped multi-digraph on 775 vertices
The above numbers confirm what dan_fulea obtain.
Then, you may want to use my optional package to visualize it (with dot2tex and graphviz installed):
sage -pip install slabbe
sage -i dot2tex
and then:
sage: from slabbe import TikzPicture
sage: G = the_rec_enum_set(20).to_digraph()
sage: tikz = TikzPicture.from_graph(G)
sage: tikz.pdf()
If your structure is really a tree (or a forest), then use
sage: R = RecursivelyEnumeratedSet(seed, succ, structure='forest')
which will allow you to enumerate the vectors in parallel using map reduce algorithms written by Florent Hivert. In any case, first consult the documentation I have written:
sage: RecursivelyEnumeratedSet?
Tell me if you have any comment, I intend to improve this module in a near future.
 | 14 | No.14 Revision |
I think you want to use RecursivelyEnumeratedSet in sage which consist in applying iteratively a successor function to a set of initial seeds:
sage: v = matrix(4,1,(1,0,0,0))
sage: v.set_immutable()
sage: seed = [v]
sage: T1 = matrix( ZZ, 4, [ -1,0,0,0, 2, 1,0,0, 4,0, 1,0, 4, 0,0, 1 ] )
sage: T2 = matrix( ZZ, 4, [ 1,2,0,0, 0,-1,0,0, 0,4, 1,0, 0, 4,0, 1 ] )
sage: T3 = matrix( ZZ, 4, [ 1,0,1,0, 0, 1,1,0, 0,0,-1,0, 0, 0,0, 1 ] )
sage: T4 = matrix( ZZ, 4, [ 1,6,0,6, 0, 3,0,2, 0,4, 1,4, 0,-4,0,-3 ] )
sage: T5 = matrix( ZZ, 4, [ 3,0,0,2, 6, 1,0,6, 4,0, 1,4, -4, 0,0,-3 ] )
sage: thin_group = [T1, T2, T3, T4, T5]
sage: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: ans.append(m_u)
....: return ans
....:
sage: R = RecursivelyEnumeratedSet(seed, succ, max_depth=4)
sage: R
A recursively enumerated set (breadth first search) with max_depth=4
To get a finite set, you may want to use max_depth as above or hmax as you suggest:
sage: def the_rec_enum_set(hmax):
....: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: if max(map(abs, m_u)) < hmax:
....: ans.append(m_u)
....: return ans
....: R = RecursivelyEnumeratedSet(seed, succ)
....: return R
....:
sage: the_rec_enum_set(20)
A recursively enumerated set (breadth first search)
The recursively enumerated set can be enumerated in different maner (look at the documentation). What I like the most is to create the generated graph:
sage: G = the_rec_enum_set(20).to_digraph(); G
Looped multi-digraph on 10 vertices
sage: G = the_rec_enum_set(50).to_digraph(); G
Looped multi-digraph on 37 vertices
sage: G = the_rec_enum_set(500).to_digraph(); G
Looped multi-digraph on 775 vertices
The above numbers confirm what dan_fulea obtain.
Then, you may want to use my optional package to visualize it (with dot2tex and graphviz installed):
sage -pip install slabbe
sage -i dot2tex
and then:
sage: from slabbe import TikzPicture
sage: G = the_rec_enum_set(20).to_digraph()
sage: tikz = TikzPicture.from_graph(G)
sage: tikz.pdf()
tikz.pdf() # or tikz.png() or tikz.svg()

If your structure is really a tree (or a forest), then use
sage: R = RecursivelyEnumeratedSet(seed, succ, structure='forest')
which will allow you to enumerate the vectors in parallel using map reduce algorithms written by Florent Hivert. In any case, first consult the documentation I have written:
sage: RecursivelyEnumeratedSet?
Tell me if you have any comment, I intend to improve this module in a near future.
 | 15 | No.15 Revision |
I think you want to use RecursivelyEnumeratedSet in sage which consist in applying iteratively a successor function to a set of initial seeds:
sage: v = matrix(4,1,(1,0,0,0))
sage: v.set_immutable()
sage: seed = [v]
sage: T1 = matrix( ZZ, 4, [ -1,0,0,0, 2, 1,0,0, 4,0, 1,0, 4, 0,0, 1 ] )
sage: T2 = matrix( ZZ, 4, [ 1,2,0,0, 0,-1,0,0, 0,4, 1,0, 0, 4,0, 1 ] )
sage: T3 = matrix( ZZ, 4, [ 1,0,1,0, 0, 1,1,0, 0,0,-1,0, 0, 0,0, 1 ] )
sage: T4 = matrix( ZZ, 4, [ 1,6,0,6, 0, 3,0,2, 0,4, 1,4, 0,-4,0,-3 ] )
sage: T5 = matrix( ZZ, 4, [ 3,0,0,2, 6, 1,0,6, 4,0, 1,4, -4, 0,0,-3 ] )
sage: thin_group = [T1, T2, T3, T4, T5]
sage: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: ans.append(m_u)
....: return ans
....:
sage: R = RecursivelyEnumeratedSet(seed, succ, max_depth=4)
sage: R
A recursively enumerated set (breadth first search) with max_depth=4
To get a finite set, you may want to use max_depth as above or hmax as you suggest:
sage: def the_rec_enum_set(hmax):
....: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: if max(map(abs, m_u)) < hmax:
....: ans.append(m_u)
....: return ans
....: R = RecursivelyEnumeratedSet(seed, succ)
....: return R
....:
sage: the_rec_enum_set(20)
A recursively enumerated set (breadth first search)
The recursively enumerated set can be enumerated in different maner (look at the documentation). What I like the most is to create the generated graph:
sage: G = the_rec_enum_set(20).to_digraph(); G
Looped multi-digraph on 10 vertices
sage: G = the_rec_enum_set(50).to_digraph(); G
Looped multi-digraph on 37 vertices
sage: G = the_rec_enum_set(500).to_digraph(); G
Looped multi-digraph on 775 vertices
The above numbers confirm what dan_fulea obtain.
Then, you may want to use my optional package to visualize it (with dot2tex and graphviz installed):
sage -pip install slabbe
sage -i dot2tex
and then:
sage: from slabbe import TikzPicture
sage: G = the_rec_enum_set(20).to_digraph()
sage: tikz = TikzPicture.from_graph(G)
sage: tikz.pdf() # or tikz.png() or tikz.svg()

If your structure is really a tree (or a forest), then use
sage: R = RecursivelyEnumeratedSet(seed, succ, structure='forest')
which will allow you to enumerate the vectors in parallel using fast map reduce algorithms written by Florent Hivert. In any case, first consult the documentation I have written:
sage: RecursivelyEnumeratedSet?
Tell me if you have any comment, I intend to improve this module in a near future.
 | 16 | No.16 Revision |
I think you want to use RecursivelyEnumeratedSet in sage which consist in applying iteratively a successor function to a set of initial seeds:
sage: v = matrix(4,1,(1,0,0,0))
sage: v.set_immutable()
sage: seed = [v]
sage: T1 = matrix( ZZ, 4, [ -1,0,0,0, 2, 1,0,0, 4,0, 1,0, 4, 0,0, 1 ] )
sage: T2 = matrix( ZZ, 4, [ 1,2,0,0, 0,-1,0,0, 0,4, 1,0, 0, 4,0, 1 ] )
sage: T3 = matrix( ZZ, 4, [ 1,0,1,0, 0, 1,1,0, 0,0,-1,0, 0, 0,0, 1 ] )
sage: T4 = matrix( ZZ, 4, [ 1,6,0,6, 0, 3,0,2, 0,4, 1,4, 0,-4,0,-3 ] )
sage: T5 = matrix( ZZ, 4, [ 3,0,0,2, 6, 1,0,6, 4,0, 1,4, -4, 0,0,-3 ] )
sage: thin_group = [T1, T2, T3, T4, T5]
sage: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: ans.append(m_u)
....: return ans
....:
sage: R = RecursivelyEnumeratedSet(seed, succ, max_depth=4)
sage: R
A recursively enumerated set (breadth first search) with max_depth=4
To get a finite set, you may want to use max_depth as above or hmax as you suggest:
sage: def the_rec_enum_set(hmax):
....: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: if max(map(abs, m_u)) < hmax:
....: ans.append(m_u)
....: return ans
....: R = RecursivelyEnumeratedSet(seed, succ)
....: return R
....:
sage: the_rec_enum_set(20)
A recursively enumerated set (breadth first search)
The recursively enumerated set can be enumerated in different maner (look at the documentation). What I like the most is to create the generated graph:
sage: G = the_rec_enum_set(20).to_digraph(); G
Looped multi-digraph on 10 vertices
sage: G = the_rec_enum_set(50).to_digraph(); G
Looped multi-digraph on 37 vertices
sage: G = the_rec_enum_set(500).to_digraph(); G
Looped multi-digraph on 775 vertices
The above numbers confirm what dan_fulea obtain.
Then, you may want to use my optional package to visualize it (with dot2tex and graphviz installed):
sage -pip install slabbe
sage -i dot2tex
and then:
sage: from slabbe import TikzPicture
sage: G = the_rec_enum_set(20).to_digraph()
sage: tikz = TikzPicture.from_graph(G)
sage: tikz.pdf() # or tikz.png() or tikz.svg()

Looking at the picture, your structure looks to be symmetric (y is a successor of x if and only if x is a successor of y). If so, use
sage: R = RecursivelyEnumeratedSet(seed, succ, structure='symmetric')
which allows to enumerate all elements without keeping all of them in memory. Even better, if your structure is really a tree (or or a forest), forest (the loop at the root can be avoided in the succ function), then use
sage: R = RecursivelyEnumeratedSet(seed, succ, structure='forest')
which will allow you to enumerate the vectors in parallel using fast map reduce algorithms written by Florent Hivert. In any case, first consult the documentation I have written:
sage: RecursivelyEnumeratedSet?
Tell me if you have any comment, I intend to improve this module in a near future.
 | 17 | No.17 Revision |
I think you want to use RecursivelyEnumeratedSet in sage which consist in applying iteratively a successor function to a set of initial seeds:
sage: v = matrix(4,1,(1,0,0,0))
sage: v.set_immutable()
sage: seed = [v]
sage: T1 = matrix( ZZ, 4, [ -1,0,0,0, 2, 1,0,0, 4,0, 1,0, 4, 0,0, 1 ] )
sage: T2 = matrix( ZZ, 4, [ 1,2,0,0, 0,-1,0,0, 0,4, 1,0, 0, 4,0, 1 ] )
sage: T3 = matrix( ZZ, 4, [ 1,0,1,0, 0, 1,1,0, 0,0,-1,0, 0, 0,0, 1 ] )
sage: T4 = matrix( ZZ, 4, [ 1,6,0,6, 0, 3,0,2, 0,4, 1,4, 0,-4,0,-3 ] )
sage: T5 = matrix( ZZ, 4, [ 3,0,0,2, 6, 1,0,6, 4,0, 1,4, -4, 0,0,-3 ] )
sage: thin_group = [T1, T2, T3, T4, T5]
sage: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: ans.append(m_u)
....: return ans
....:
sage: R = RecursivelyEnumeratedSet(seed, succ, max_depth=4)
sage: R
A recursively enumerated set (breadth first search) with max_depth=4
To get a finite set, you may want to use max_depth as above or hmax as you suggest:
sage: def the_rec_enum_set(hmax):
....: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: if max(map(abs, m_u)) < hmax:
....: ans.append(m_u)
....: return ans
....: R = RecursivelyEnumeratedSet(seed, succ)
....: return R
....:
sage: the_rec_enum_set(20)
A recursively enumerated set (breadth first search)
The recursively enumerated set can be enumerated in different maner (look at the documentation). What I like the most is to create the generated graph:
sage: G = the_rec_enum_set(20).to_digraph(); G
Looped multi-digraph on 10 vertices
sage: G = the_rec_enum_set(50).to_digraph(); G
Looped multi-digraph on 37 vertices
sage: G = the_rec_enum_set(500).to_digraph(); G
Looped multi-digraph on 775 vertices
The above numbers confirm what dan_fulea obtain.
Then, you may want to use my optional package to visualize it (with dot2tex and graphviz installed):
sage -pip install slabbe
sage -i dot2tex
and then:
sage: from slabbe import TikzPicture
sage: G = the_rec_enum_set(20).to_digraph()
sage: tikz = TikzPicture.from_graph(G)
sage: tikz.pdf() # or tikz.png() or tikz.svg()

Looking at the picture, your structure looks to be symmetric (y is a successor of x if and only if x is a successor of y). If so, use
sage: R = RecursivelyEnumeratedSet(seed, succ, structure='symmetric')
which allows to enumerate all elements without keeping all of them in memory. Even better, if your structure is really a tree or a forest (the (that is if you are able to avoid backward arrows and any loop at in the root can be avoided in the succ successor function), then use
sage: R = RecursivelyEnumeratedSet(seed, succ, structure='forest')
which will allow you to enumerate the vectors in parallel using fast map reduce algorithms written by Florent Hivert. In any case, first consult the documentation I have written:
sage: RecursivelyEnumeratedSet?
Tell me if you have any comment, I intend to improve this module in a near future.
 | 18 | No.18 Revision |
I think you want to use RecursivelyEnumeratedSet in sage which consist in applying iteratively a successor function to a set of initial seeds:
sage: v = matrix(4,1,(1,0,0,0))
sage: v.set_immutable()
sage: seed = [v]
sage: T1 = matrix( ZZ, 4, [ -1,0,0,0, 2, 1,0,0, 4,0, 1,0, 4, 0,0, 1 ] )
sage: T2 = matrix( ZZ, 4, [ 1,2,0,0, 0,-1,0,0, 0,4, 1,0, 0, 4,0, 1 ] )
sage: T3 = matrix( ZZ, 4, [ 1,0,1,0, 0, 1,1,0, 0,0,-1,0, 0, 0,0, 1 ] )
sage: T4 = matrix( ZZ, 4, [ 1,6,0,6, 0, 3,0,2, 0,4, 1,4, 0,-4,0,-3 ] )
sage: T5 = matrix( ZZ, 4, [ 3,0,0,2, 6, 1,0,6, 4,0, 1,4, -4, 0,0,-3 ] )
sage: thin_group = [T1, T2, T3, T4, T5]
sage: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: ans.append(m_u)
....: return ans
....:
sage: R = RecursivelyEnumeratedSet(seed, succ, max_depth=4)
sage: R
A recursively enumerated set (breadth first search) with max_depth=4
To get a finite set, you may want to use max_depth as above or hmax as you suggest:
sage: def the_rec_enum_set(hmax):
....: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: if max(map(abs, m_u)) < hmax:
....: ans.append(m_u)
....: return ans
....: R = RecursivelyEnumeratedSet(seed, succ)
....: return R
....:
sage: the_rec_enum_set(20)
A recursively enumerated set (breadth first search)
The recursively enumerated set can be enumerated in different maner (look at the documentation). What I like the most is to create the generated graph:
sage: G = the_rec_enum_set(20).to_digraph(); G
Looped multi-digraph on 10 vertices
sage: G = the_rec_enum_set(50).to_digraph(); G
Looped multi-digraph on 37 vertices
sage: G = the_rec_enum_set(500).to_digraph(); G
Looped multi-digraph on 775 vertices
The above numbers confirm what dan_fulea obtain.
Then, you may want to use my optional package to visualize it (with dot2tex and graphviz installed):
sage -pip install slabbe
sage -i dot2tex
and then:
sage: from slabbe import TikzPicture
sage: G = the_rec_enum_set(20).to_digraph()
sage: tikz = TikzPicture.from_graph(G)
sage: tikz.pdf() # or tikz.png() or tikz.svg()

Looking at the picture, your structure looks to be symmetric (y is a successor of x if and only if x is a successor of y). If so, use
sage: R = RecursivelyEnumeratedSet(seed, succ, structure='symmetric')
which allows to enumerate all elements without keeping all of them in memory. Even better, if your structure is really a tree or a forest (that is if you are able to avoid backward arrows and any loop in the successor function), then use
sage: R = RecursivelyEnumeratedSet(seed, succ, structure='forest')
which will allow you to enumerate the vectors in parallel using fast map reduce algorithms written by Florent Hivert. In any case, first consult the documentation I have written:
sage: RecursivelyEnumeratedSet?
One information that is missing in the graph is the label of the edges. One way to solve this is to momentarily hide the label information inside the arrival vertex. Once, the graph is made, we put back the information into the edge. I usually do like this:
sage: seed = [(v,None)]
sage: def the_rec_enum_set(hmax):
....: def succ(node):
....: u,label = node
....: ans = []
....: for i,m in zip([1,2,3,4,5], thin_group):
....: m_u = m*u
....: m_u.set_immutable()
....: if max(map(abs, m_u)) < hmax:
....: ans.append((m_u,i))
....: return ans
....: R = RecursivelyEnumeratedSet(seed, succ)
....: return R
....:
sage: R = the_rec_enum_set(20)
sage: R.to_digraph()
Looped multi-digraph on 22 vertices
sage: G = R.to_digraph()
sage: G
Looped multi-digraph on 22 vertices
sage: from slabbe.graph import digraph_move_label_to_edge
sage: GG = digraph_move_label_to_edge(G)
sage: GG
Looped digraph on 10 vertices
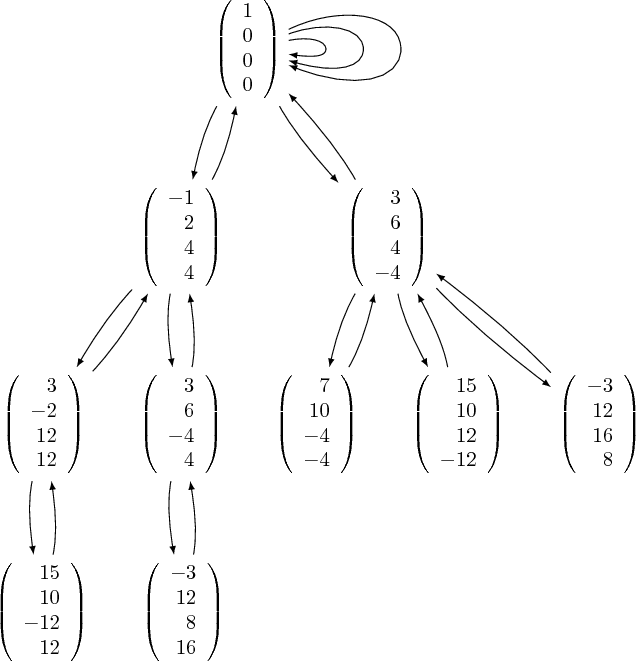
sage: TikzPicture.from_graph(GG).pdf()
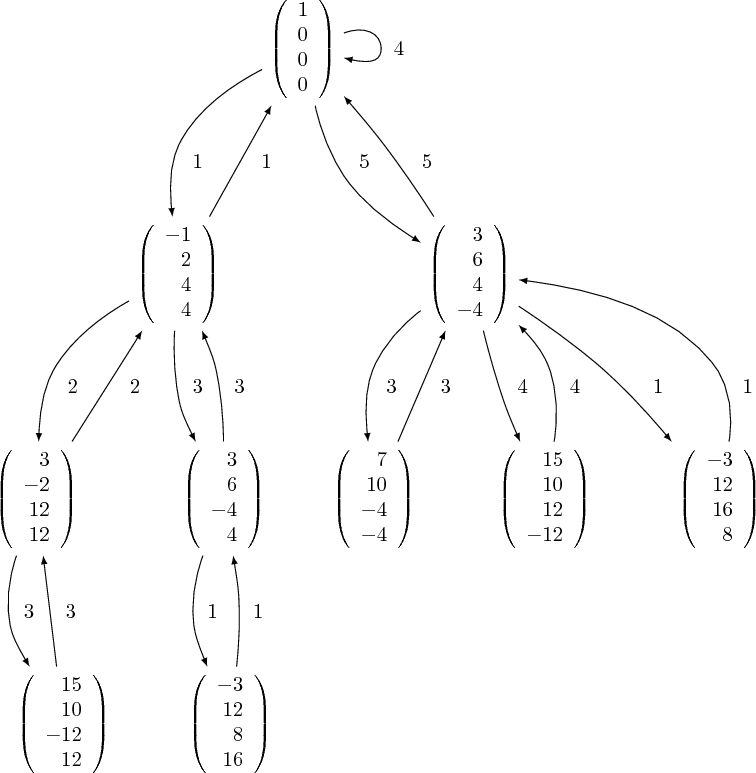
I intend to move this feature directly in Sage once I have time. Tell me if you have any other comment, I intend to improve this module in a near future.
 | 19 | No.19 Revision |
I think you want to use RecursivelyEnumeratedSet in sage which consist in applying iteratively a successor function to a set of initial seeds:
sage: v = matrix(4,1,(1,0,0,0))
sage: v.set_immutable()
sage: seed = [v]
sage: T1 = matrix( ZZ, 4, [ -1,0,0,0, 2, 1,0,0, 4,0, 1,0, 4, 0,0, 1 ] )
sage: T2 = matrix( ZZ, 4, [ 1,2,0,0, 0,-1,0,0, 0,4, 1,0, 0, 4,0, 1 ] )
sage: T3 = matrix( ZZ, 4, [ 1,0,1,0, 0, 1,1,0, 0,0,-1,0, 0, 0,0, 1 ] )
sage: T4 = matrix( ZZ, 4, [ 1,6,0,6, 0, 3,0,2, 0,4, 1,4, 0,-4,0,-3 ] )
sage: T5 = matrix( ZZ, 4, [ 3,0,0,2, 6, 1,0,6, 4,0, 1,4, -4, 0,0,-3 ] )
sage: thin_group = [T1, T2, T3, T4, T5]
sage: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: ans.append(m_u)
....: return ans
....:
sage: R = RecursivelyEnumeratedSet(seed, succ, max_depth=4)
sage: R
A recursively enumerated set (breadth first search) with max_depth=4
To get a finite set, you may want to use max_depth as above or hmax as you suggest:
sage: def the_rec_enum_set(hmax):
....: def succ(u):
....: ans = []
....: for m in thin_group:
....: m_u = m*u
....: m_u.set_immutable()
....: if max(map(abs, m_u)) < hmax:
....: ans.append(m_u)
....: return ans
....: R = RecursivelyEnumeratedSet(seed, succ)
....: return R
....:
sage: the_rec_enum_set(20)
A recursively enumerated set (breadth first search)
The recursively enumerated set can be enumerated in different maner (look at the documentation). What I like the most is to create the generated graph:
sage: G = the_rec_enum_set(20).to_digraph(); G
Looped multi-digraph on 10 vertices
sage: G = the_rec_enum_set(50).to_digraph(); G
Looped multi-digraph on 37 vertices
sage: G = the_rec_enum_set(500).to_digraph(); G
Looped multi-digraph on 775 vertices
The above numbers confirm what dan_fulea obtain.
Then, you may want to use my optional package to visualize it (with dot2tex and graphviz installed):
sage -pip install slabbe
sage -i dot2tex
and then:
sage: from slabbe import TikzPicture
sage: G = the_rec_enum_set(20).to_digraph()
sage: tikz = TikzPicture.from_graph(G)
sage: tikz.pdf() # or tikz.png() or tikz.svg()

Looking at the picture, your structure looks to be symmetric (y is a successor of x if and only if x is a successor of y). If so, use
sage: R = RecursivelyEnumeratedSet(seed, succ, structure='symmetric')
which allows to enumerate all elements without keeping all of them in memory. Even better, if your structure is really a tree or a forest (that is if you are able to avoid backward arrows and any loop in the successor function), then use
sage: R = RecursivelyEnumeratedSet(seed, succ, structure='forest')
which will allow you to enumerate the vectors in parallel using fast map reduce algorithms written by Florent Hivert. without keeping the elements in memory. In any case, first consult the documentation I have written:
sage: RecursivelyEnumeratedSet?
One information that is missing in the graph is the label of the edges. One way to solve this is to momentarily hide the label information inside the arrival vertex. Once, the graph is made, we put back the information into the edge. I usually do like this:
sage: seed = [(v,None)]
sage: def the_rec_enum_set(hmax):
....: def succ(node):
....: u,label = node
....: ans = []
....: for i,m in zip([1,2,3,4,5], thin_group):
....: m_u = m*u
....: m_u.set_immutable()
....: if max(map(abs, m_u)) < hmax:
....: ans.append((m_u,i))
....: return ans
....: R = RecursivelyEnumeratedSet(seed, succ)
....: return R
....:
sage: R = the_rec_enum_set(20)
sage: R.to_digraph()
Looped multi-digraph on 22 vertices
sage: G = R.to_digraph()
sage: G
Looped multi-digraph on 22 vertices
sage: from slabbe.graph import digraph_move_label_to_edge
sage: GG = digraph_move_label_to_edge(G)
sage: GG
Looped digraph on 10 vertices
sage: TikzPicture.from_graph(GG).pdf()

I intend to move this feature directly in Sage once I have time. Tell me if you have any other comment, I intend to improve this module in a near future.
