continuous Fourier transform

edit

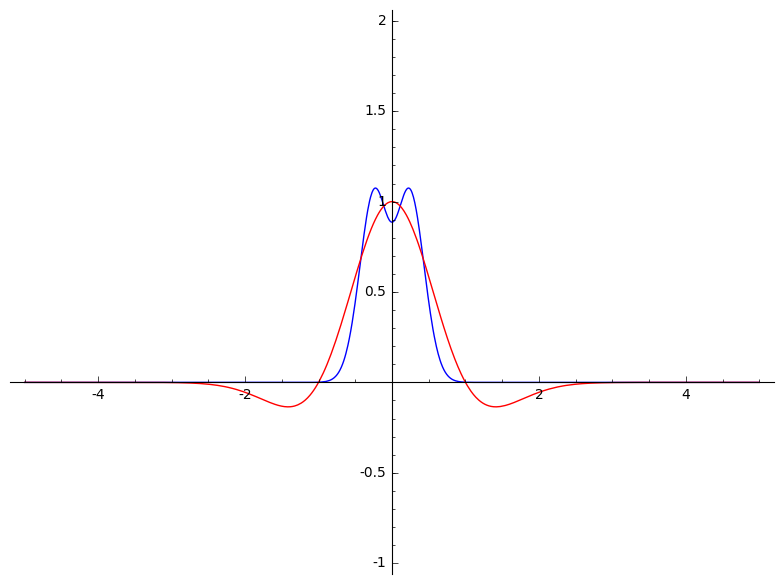
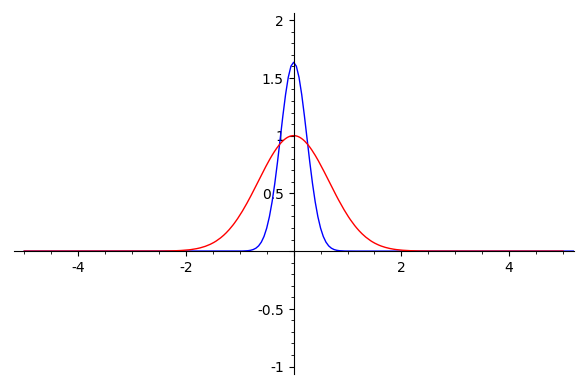
Well...FWIW:

sage: var("t, omega")
(t, omega)
sage: from sympy.integrals.transforms import fourier_transform as sft
sage: from sympy.integrals.transforms import inverse_fourier_transform as isft
sage: sft?

Signature:      sft(f, x, k, **hints)
Docstring:     
   Compute the unitary, ordinary-frequency Fourier transform of f,
   defined as

      F(k) = int_{-infty}^infty f(x) e^{-2pi i x k} d x.    Signature:      sft(f, x, k, **hints)
Docstring:     
   Compute the unitary, ordinary-frequency Fourier transform of f,
   defined as

      F(k) = int_{-infty}^infty f(x) e^{-2pi i x k} d x.

   If the transform cannot be computed in closed form, this function
   returns an unevaluated "FourierTransform" object.

   For other Fourier transform conventions, see the function
   "sympy.integrals.transforms._fourier_transform()".

   For a description of possible hints, refer to the docstring of
   "sympy.integrals.transforms.IntegralTransform.doit()". Note that
   for this transform, by default "noconds=True".    

   If the transform cannot be computed in closed form, this function
   returns an unevaluated "FourierTransform" object.

   For other Fourier transform conventions, see the function
   "sympy.integrals.transforms._fourier_transform()".

   For a description of possible hints, refer to the docstring of
   "sympy.integrals.transforms.IntegralTransform.doit()". Note that
   for this transform, by default "noconds=True".

[ Abriged...]

sage: sft(e^(-t^2)*(1-t^2), t, omega)._sage_()
1/2*sqrt(pi)*(2*pi^2*omega^2 + 1)*e^(-pi^2*omega^2)
sage: isft(sft(e^(-t^2)*(1-t^2), t, omega)._sage_(), omega, t)._sage_()
-(t^2 - 1)*e^(-t^2)

EDITED : The case you propose seems hard to integrate: sympy doesn't return a result for your second case. BTW, neither maxima, sympy, fricas nor giac are able to compute the integral directly. Neither does mathematica, which seems to be able to compute the Fourier integral by less direct means :

sage: mathematica.Integrate(g(t)*e^(-2*I*pi*t*o),[t,-oo,oo])
Integrate[(E^((-2*I)*o*Pi*t - t^2)*Sin[t])/t, {t, -Infinity, Infinity}]
sage: mathematica.FourierTransform(e^(-t^2)*sin(t)/t, t, omega).sage()
1/2*sqrt(1/2)*sqrt(pi)*erf(1/2*omega + 1/2) + 1/2*sqrt(1/2)*sqrt(pi)*erf(-1/2*omega + 1/2)

WARNING All the engines do not follow the same conventins for Fourier transform parameters. See Wikipedia for alternatives...

HTH,

At least you can always take a naive numerical approach:

F = lambda x: exp(-x^2)*sin(x)/x
plot2 = plot(F, xmin = -5, xmax = 5, color = 'red')
### continuous Fourier transform on RR
fhat_real = lambda xi: numerical_integral(lambda x: (F(x)*exp(-2*pi*I*x*xi)).real_part(),-oo,oo, eps_abs=1e-3, eps_rel=1e-3)[0]
import numpy
plot1 = list_plot([(x,fhat_real(x)) for x in numpy.arange(-5,5, step=0.05)], plotjoined=True)
show(plot1 + plot2, xmin = -5, xmax = 5, ymin = -1, ymax = 2)

Output: